
(b)“正、负上下分” 因F,(x,y)>0,(x,y)∈S,故x∈[x-B,x+B], 把F(x,y)看作y的函数,它在yo-B,yo+B]上 严格增,且连续(据条件(①)). 特别对于函数F(x,y),由条 件F(xo,y0)=0可知 F(xo,o+B)>0, F(xo,o-B)<0. 前页 后 返回
前页 后页 返回 0 0 F x y ( , ) 0, (b) “正、负上下分 ” F (x, y) 0, (x, y) S, y [ , ], 因 故 x x0 x0 F(x, y) y [ , ] 把 看作 的函数,它在 y0 y0 上 严格增,且连续 ( 据条件 (i) ). 0 特别对于函数 F x y ( , ), 由条 0 0 件 可知 F x y ( , ) 0 0 0 F x y ( , ) 0.

(c)“同号两边伸” 因为F(x,-B),F(x,o+B)关于x连续,故由 (b)的结论,根据保号性,x(0<a≤B),使得 F(x,y+B)>0, F(x,yo-B)<0, x∈(x0-a,x0+a). (d“利用介值性” V∈(x-a,x+a),因F(e,y)关于y连续,且严 格增,故由()的结论,依据介值性定理,存在惟 前页 后页
前页 后页 返回 因为 ( , ), ( , ) 关于 连续,故由 F x y0 F x y0 x (b) 的结论,根据保号性, (0 ), 使得 0 F x y ( , ) 0, (c) “同号两边伸” (d) “利用介值性” ˆ ( , ) , x x0 x0 因 F(x ˆ , y) 关于 y 连续, 且严 格增,故由 (c) 的结论,依据介值性定理, 存在惟 0 F x y ( , ) 0, 0 0 x x x ( , ).
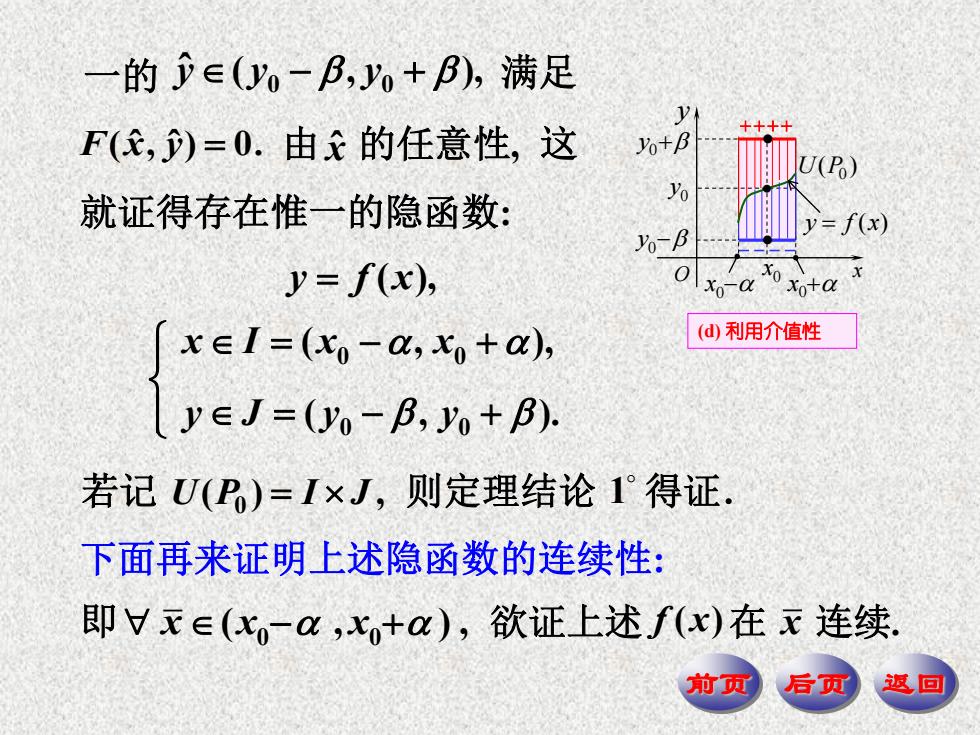
一的∈(y-B,yo+),满足 F(e,)=0.由的任意性,这 %+B U(P) 就证得存在惟一的隐函数: =f(x Yo-B y=f(x), 0 xo+a x∈I=(c-a,xo+a), (d)利用介值性 y∈J=(yo-B,y+B) 若记U(P)=I×J,则定理结论1°得证. 下面再来证明上述隐函数的连续性: 即Vx∈(x-ax,+a),欲证上述f(x)在x连续. 前
前页 后页 返回 (d) 利用介值性 ++++ - - - - x 0 x y 0 y O 0 x 0 x 0 U P( ) 0 y 0 y y f x ( ) 一的 y y y ˆ ( , ), 0 0 满足 就证得存在惟一的隐函数: F(x ˆ , y ˆ) 0. 由 x ˆ 的任意性, 这 0 0 0 0 ( , ), ( , ). x I x x y J y y ( ) , U P0 I J 若记 则定理结论 1 得证. 下面再来证明上述隐函数的连续性: 0 0 即 x x x ( , ) , 欲证上述 f (x) 在 x 连续. y f x ( )
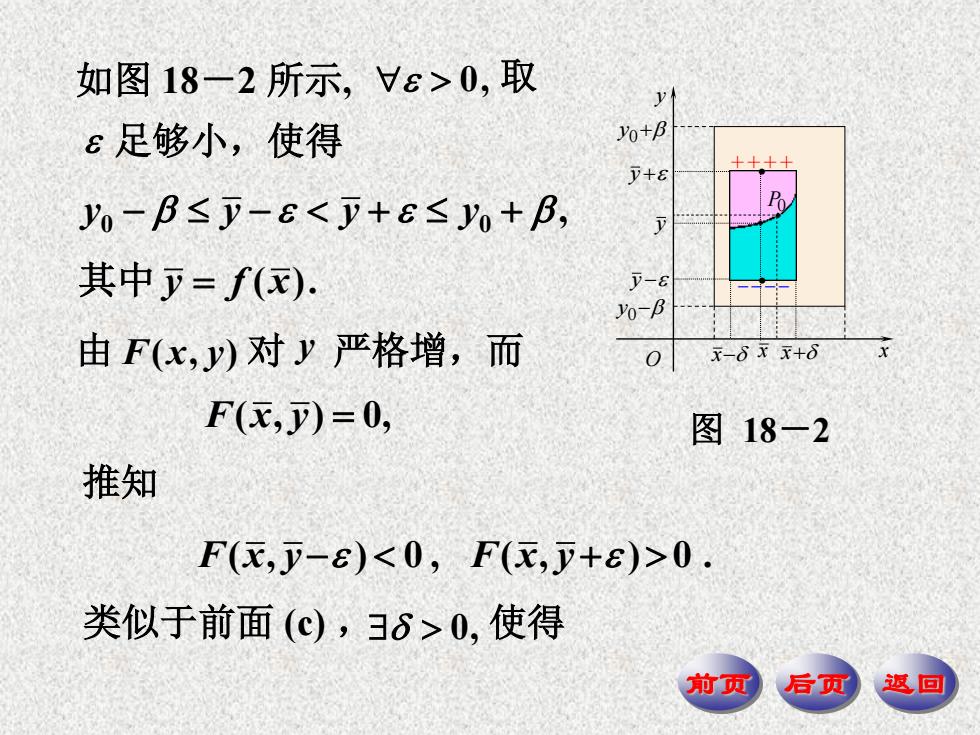
如图18-2所示,Vε>0,取 y ε足够小,使得 YO+B y+8 y0-B≤)-E<F+ε≤y0+B, 其中少=f() -8 0-B 由F(x,y)对y严格增,而 0 x-8xx+8 F(衣,)=0, 图18一2 推知 F(c,-8)<0,F(x,+8)>0. 类似于前面(c),3δ>0,使得 前页 后页 返回
前页 后页 返回 0 0 y y y y , F x y F x y ( , ) 0 , ( , ) 0 . 类似于前面 (c) , 0, 使得 F x y ( , ) 0, 由 F( x , y) 对 y 严格增,而 其中 y f x ( ). 推知 . . x x O y x x y y y y0 y0 ++++ ---- P0 . . 图 18-2 足够小,使得 如图 18-2 所示, 0, 取

(c-6,x+6)c(x0-a,xo+a), 且当x∈(c-6,x+6)时,有 F(x,y-8)<0,F(x,y+8)>0. 类似于前面(d),由于隐函数惟一,故有 D-6<f(x)<D+8,x∈(c-6,x+6) 因此f(x)在x连续.由x的任意性,便证得f(x) 在(x。-a,x+a)上处处连续。 前页 后页 返回
前页 后页 返回 ( , ) ( , ), x x x0 x0 F(x, y ) 0, F(x, y ) 0. y f (x) y , x(x , x ), 在 (x0 , x0 ) 上处处连续. 因此 f (x) 在 x 连续. 由 x 的任意性, 便证得 f (x) 且当 x(x , x ) 时,有 类似于前面 (d) ,由于隐函数惟一,故有