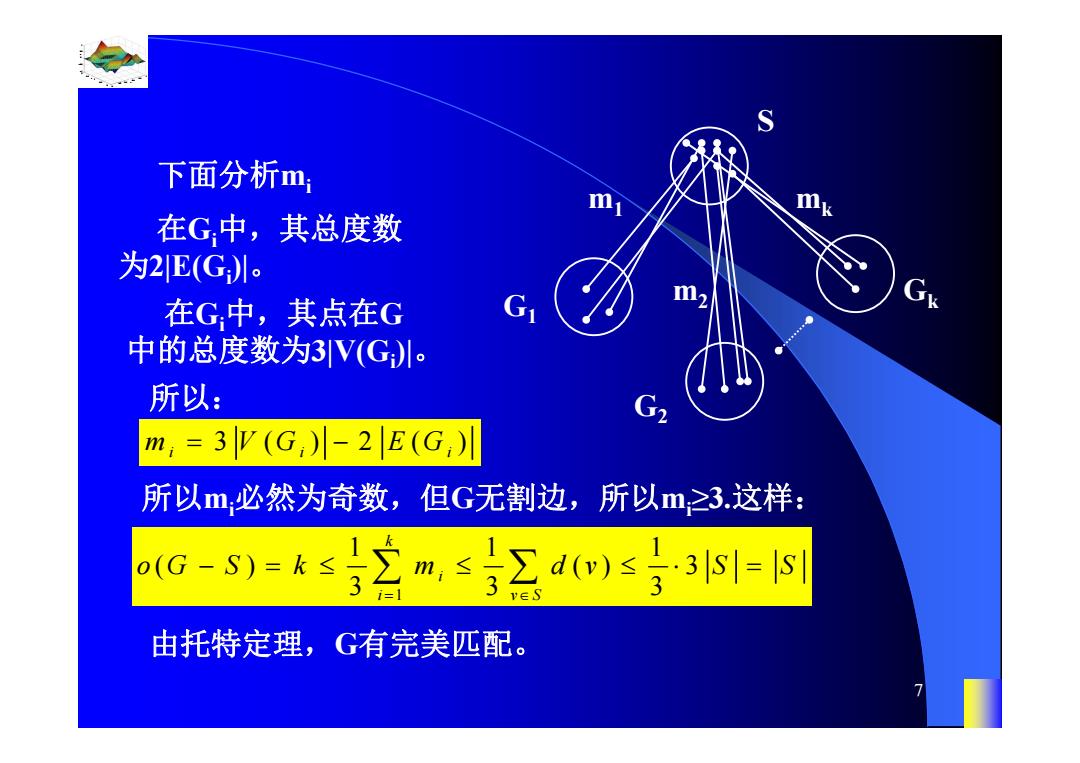
下面分析m mk 在G,中,其总度数 为2E(G1。 在G中,其点在G G 中的总度数为3V(Gl。 所以: G2 m,=3Ψ(G,)川-2lE(G;) 所以m必然为奇数,但G无割边,所以m≥3.这样: o(G-S)=k≤3∑m,≤3∑d)≤33小s到=小s 由托特定理,G有完美匹配
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 7 下面分析mi S G1 G2 Gk m1 m2 mk 在Gi中,其总度数 为2|E(Gi)|。 在Gi中,其点在G 中的总度数为3|V(Gi)|。 所以: 3()2() m VG EG ii i 所以mi必然为奇数,但G无割边,所以mi≥3.这样: 1 11 1 ( ) () 3 33 3 k i i vS oG S k m d v S S 由托特定理,G有完美匹配
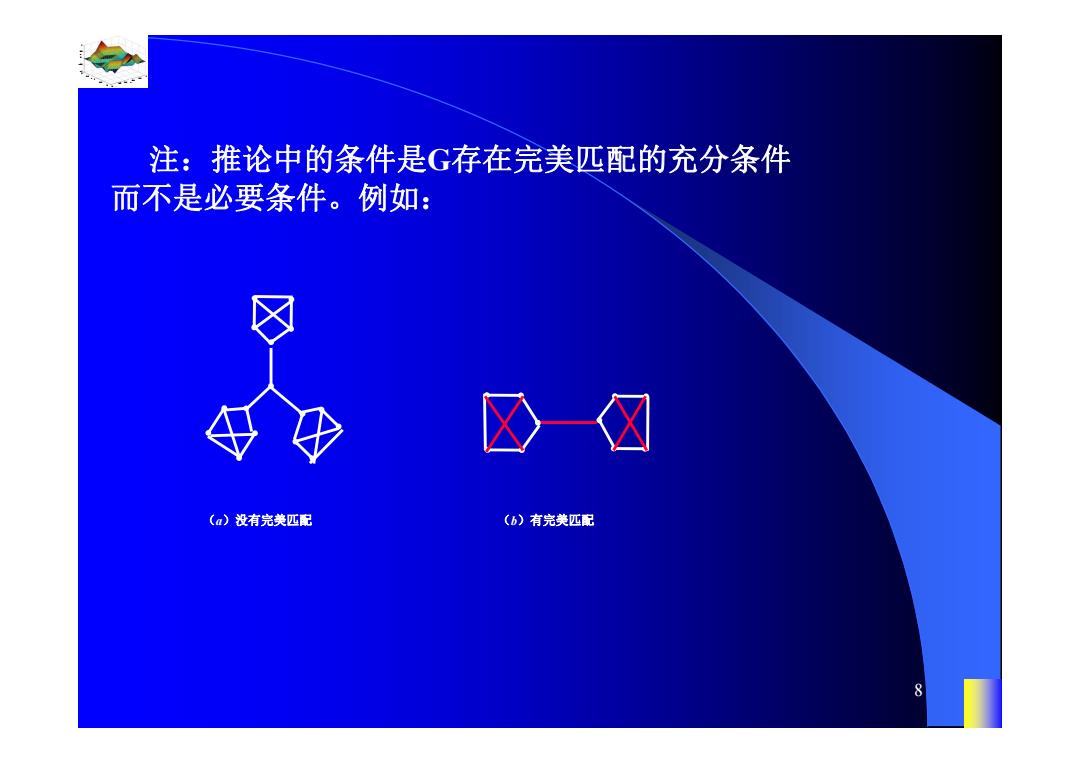
注:推论中的条件是G存在完美匹配的充分条件 而不是必要条件。例如: (a)没有完美匹配 (D)有完美匹配 8
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 8 注:推论中的条件是G存在完美匹配的充分条件 而不是必要条件。例如: (a)没有完美匹配 (b)有完美匹配

(二)、图的一因子分解 所谓一个图G的因子G,是指至少包含G的一条边的生成 子图。 所谓一个图G的因子分解,是指把图G分解为若干个边 不重的因子之并。 所谓一个图G的n因子,是指图G的n度正则因子
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 9 所谓一个图G的因子Gi,是指至少包含G的一条边的生成 子图。 所谓一个图G的因子分解,是指把图G分解为若干个边 不重的因子之并。 所谓一个图G的n因子,是指图G的n度正则因子。 (二)、图的一因子分解

如果一个图G能够分解为若干n因子之并,称G是可n因 子分解的。 图G1 图G2 在上图中,红色边在G,中的导出子图,是G的一个一因 子;红色边在G,中的导出子图,是G的一个二因子。 研究图的因子分解主要是两个方面:一是能否进行分解 (因子分解的存在性),二是如何分解(分解算法)。 10
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 10 如果一个图G能够分解为若干n因子之并,称G是可n因 子分解的。 图G1 在上图中,红色边在G1中的导出子图,是G的一个一因 子;红色边在G2中的导出子图,是G的一个二因子。 图G2 研究图的因子分解主要是两个方面:一是能否进行分解 (因子分解的存在性),二是如何分解(分解算法)