《数字信号处理》课程教学资源（教案讲义）ch4 IIR数字滤波器设计

4.1.2TypeIChebyshevLowpassfilter(CBI型)1H(jo)1+gC(0/0)cos(Ncos- x)[x/≤1C~(x)=cosh(N cosh- x)[x>14|H(i(の)XNNQ6：通带波纹の：通带截频N：阶数(由阻带指标确定A|H(i(の)N/1+62N-20wCBI型filter的性质1)在0≤≤时，H(j0)在1和间振荡(equiripplefilter)1+2)の≥の时，H(jの)"单调下降(N增大，下降加速)

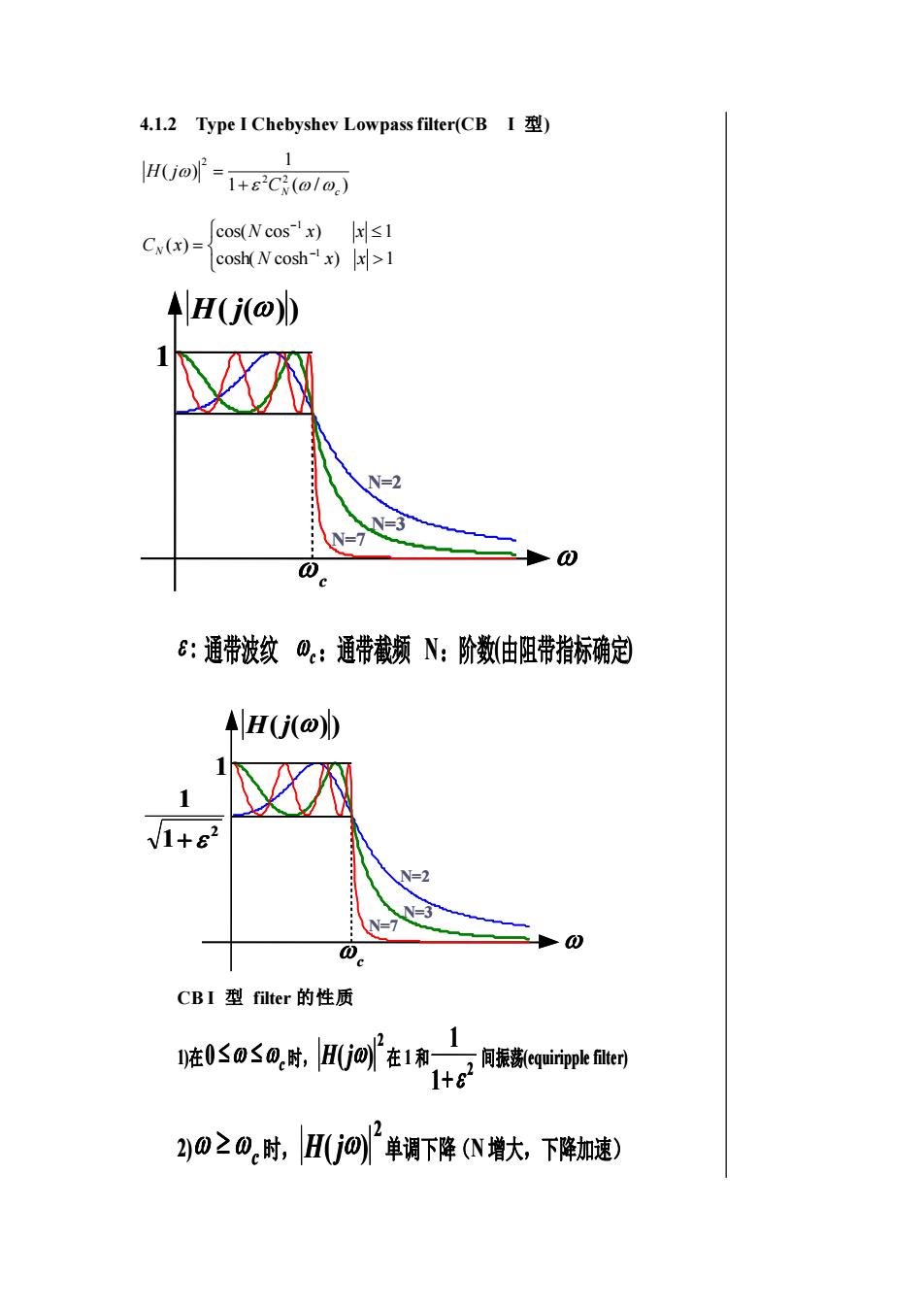
4.1.2 Type I Chebyshev Lowpass filter(CB I 型) 1 ( / ) 1 ( ) 2 2 2 CN c H j     + =      = − − cosh( cosh ) 1 cos( cos ) 1 ( ) 1 1 N x x N x x C x N  H( j()) 1  c N=2 N=3 N=7  H( j()) 1  c N=2 N=3 N=7  : 通带波纹  c：通带截频 N：阶数(由阻带指标确定)  c：通带截频 N：阶数(由阻带指标确定)  H( j()) 1  c N=2 N=3 N=7 2 1 1 +   H( j()) 1  c N=2 N=3 N=7 2 1 1 +  CB I 型 filter 的性质 1)在  c 0   时， 2 H( j) 在 1 和 2 1 1 +  1)在 间振荡(equiripple filter)  c 0    c 0   时， 2 H( j) 2 H( j) 在 1 和 2 1 1 +  间振荡(equiripple filter) 2) c    时， 2 2)   c 时， H( j) 单调下降（N 增大，下降加速） 2 H( j) 2 H( j) 单调下降（N 增大，下降加速）

>/2=—13)H(jQ)8控制了通带衰减1+2N为奇时 [H(j0)=11N为偶时 [H(j0)2 =1+2归一化CheybshevI型filter的极点St=0+ jo;k=1,2..,Nβ= sih (1/s)Oμ =-sinh( B)sin (2k-1)元N2NN/21(0 +0%)N为偶时H.o(s)s?-20s+(02 +0)V1+&21)/2sinh( β)(0 +0)N为奇时H..(s)=s +sinh( β)s?-20,s+(0 +0%)CBI型AF设计步骤1)通带截频确定0。=2)通带指标确定e-201og|H(jo.)= A,= 6= V100:14, -1]3)阻带指标确定Ncosh(- /104 -1)-20logoH(jo,)= A, = N =cosh-(o,/o.)MATLAB设计模拟typeIChebyshevfilter[z,p,k]=cheb1ap(N,Ap),确定N阶归一化的Chebyshevfilter的零点、极点和增益(gain）[num.den]=cheby1(N.Ap.Wc.'s')确定阶数为N，通带截频为Wc(radian/s)的Chebyshevfilter。's’表示模拟域[N,Wc]=cheblord(Wp,Ws,Ap,As,'s)确定模拟Chebyshevfilter的阶数N。Wc=Wp(rad/s)例：设计满足下列条件的模拟CBI型低通滤波器p=1KHz,fs=5kHz, Ap=1dB，As=40dB%filter specificationWp=2*pi*1000;Ws=2*pi*5000;Ap=1;As=40

3) 2 2 1 1 ( )   + = c 3) H j 2  控制了通带衰减 2 1 1 ( )   + = c H j 2 2 1 1 ( )   + = c H j  控制了通带衰减 N 为奇时 ( 0) 1 2 N 为奇时 H( j0) = 1 2 H( j0) = 1 2 H j = N 为偶时 2 2 1 1 ( 0) +  N 为偶时 H j = 2 2 1 1 ( 0) +  H j = 2 2 1 1 ( 0) +  H j = 归一化 Cheybshev I 型 filter 的极点 sk = k + jk ; k =1,2.,N N k k 2 (2 1) sinh( )sin    − = − N sinh (1/ ) 1   − = N 为偶时 2 ( ) ( ) 1 1 ( ) 2 2 2 / 2 2 2 1 2 0 k k k k k N k L s s H s       − + + + + = = N 为奇时 2 ( ) ( ) sinh( ) sinh( ) ( ) 2 2 2 ( 1)/ 2 2 2 1 0 k k k k k N k L s s s H s        − + + + + =  − = CB I 型 AF 设计步骤 1)通带截频确定 c  p 1)通带截频确定 =  c  p = 2)通带指标确定 e c Ap −20log H( j ) = 10 1 0.1  = − Ap  ] 3)阻带指标确定 N s As −20log10 H( j ) = cosh ( / ) 10 1) 1 cosh ( 1 1 s c As N    − − −  = MATLAB 设计模拟 type I Chebyshev filter [z,p,k]=cheb1ap(N,Ap); 确定 N 阶归一化的 Chebyshev filter 的零点、极点和增益(gain) [num,den]=cheby1(N,Ap,Wc,'s') 确定阶数为 N，通带截频为 Wc(radian/s)的 Chebyshev filter。 's' 表示模拟域 [N,Wc]=cheb1ord(Wp,Ws,Ap,As,'s') 确定模拟 Chebyshev filter 的阶数 N。Wc=Wp(rad/s) 例：设计满足下列条件的模拟 CB I 型低通滤波器 fp=1KHz, fs=5kHz, Ap=1dB, As=40dB %filter specification Wp=2*pi*1000;Ws=2*pi*5000;Ap=1;As=40;

%Computerfilterorder[N,Wc]=cheb1ord(Wp,Ws,Ap,As,'s);fprintf(Order of the filter-%.Ofln',N)%computefiltercoefficients[num,den] = cheby1(N,Ap,Wc,'s),disp(Numerator polynomial')fprintf(%.4eln',num),disp(Denominator polynomial');fprintf(%.4eln',den),%ComputeApand As ofdesignedfilteromega=[Wp Ws],h = freqs(num,den,omega);fprintf(Ap=%.4fln',-20*log10(abs(h(1);fprintf(As=%.4fin,-20*log10(abs(h(2);1.2187×10llH(s)=$+6.2099×10"s2+4.88×10's+1.2187×100-10Ap=1.0000-20As=47.8467-30-40-5060%10002000 Freohcy4Az50006000切比雪夫ⅡI型模拟低通滤波器1cC%(0. / 0)HCic1+C(0. /0)1+gC%(0. /0)A (H(jo)]1oopoMATLAB设计模拟typeIIChebyshevfilter

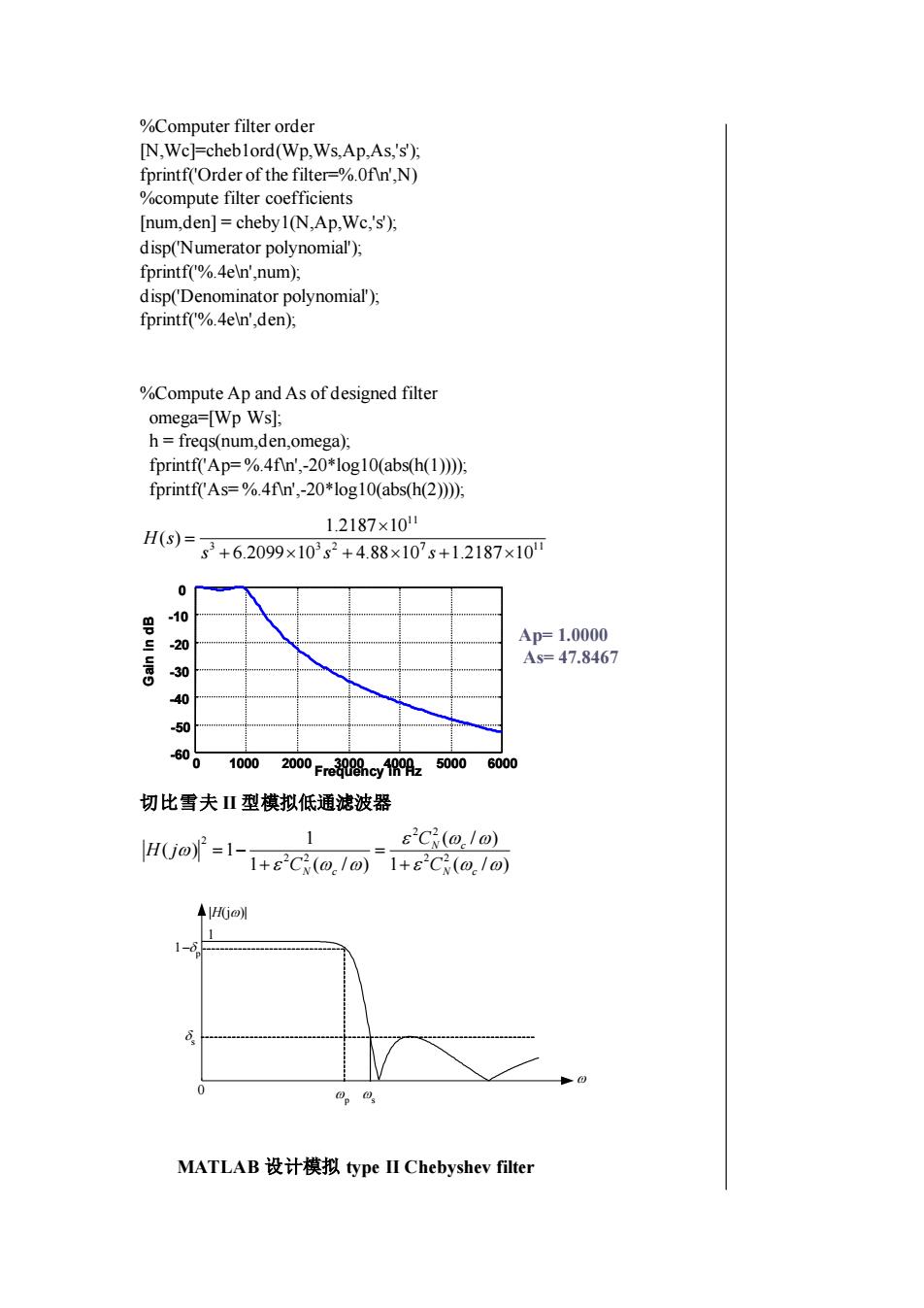
%Computer filter order [N,Wc]=cheb1ord(Wp,Ws,Ap,As,'s'); fprintf('Order of the filter=%.0f\n',N) %compute filter coefficients [num,den] = cheby1(N,Ap,Wc,'s'); disp('Numerator polynomial'); fprintf('%.4e\n',num); disp('Denominator polynomial'); fprintf('%.4e\n',den); %Compute Ap and As of designed filter omega=[Wp Ws]; h = freqs(num,den,omega); fprintf('Ap= %.4f\n',-20*log10(abs(h(1)))); fprintf('As= %.4f\n',-20*log10(abs(h(2)))); 3 3 2 7 11 11 6.2099 10 4.88 10 1.2187 10 1.2187 10 ( ) +  +  +   = s s s H s Ap= 1.0000 As= 47.8467 0 1000 2000 3000 4000 5000 6000 -60 -50 -40 -30 -20 -10 0 Frequency in Hz Gain in dB 0 1000 2000 3000 4000 5000 6000 -60 -50 -40 -30 -20 -10 0 Frequency in Hz Gain in dB 切比雪夫 II 型模拟低通滤波器 1 ( / ) ( / ) 1 ( / ) 1 ( ) 1 2 2 2 2 2 2 2           N c N c N c C C C H j + = + = − MATLAB 设计模拟 type II Chebyshev filter 1 0 p  s − p |H(j)| s

[N,Wc]=cheb2ord(Wp,Ws,Ap,As,'s)确定模拟切比雪夫II型滤波器的阶数N。[num,den]=cheby2(N,As,Wc,'s')确定阶数为N，阻带衰减为AsdB的切比雪夫II型滤波器的分子和分母多项式。Wc由cheb2ord函数确定。4.1.3椭圆低通滤波器MATLAB设计椭圆滤波器函：[N,Wc]=ellipord(Wp,Ws,Ap,As,'s)确定椭圆滤波器的阶数N。Wc=Wp。[num,den]=ellip(N,Ap,As,Wc,'s)确定阶数为N，通带参衰减为ApdB，阻带衰减为AsdB的椭圆滤波器的分子和分母多项式。Wc是椭圆滤波器的通带截频

[N,Wc]=cheb2ord(Wp,Ws,Ap,As,'s') 确定模拟切比雪夫 II 型滤波器的阶数 N。 [num,den]=cheby2(N,As,Wc,'s') 确定阶数为 N，阻带衰减为 As dB 的切比雪夫 II 型 滤波器的分子和分母多项式。Wc 由 cheb2ord 函数确定。 4.1.3 椭圆低通滤波器 MATLAB 设计椭圆滤波器函： [N,Wc]=ellipord(Wp,Ws,Ap,As,'s') 确定椭圆滤波器的阶数 N。Wc=Wp。 [num,den]=ellip(N,Ap,As,Wc,'s') 确定阶数为 N，通带参衰减为 Ap dB，阻带衰减为 As dB 的椭圆滤波器的分子和分母多项式。Wc 是椭圆滤波器的通 带截频

4.2模拟频率变换问题的提出·低通到低通的变换·低通到高通的变换。低通到带通的变换低通到带阻的变换问题的提出如何设计模拟高通、带通、带阻滤波器？4.2.1低通到低通的变换低通到低通的变换为Hp(s)= H,(3) = s / 00将s=j，s=jo代入s=s/の中得=0/04可可=0/0000p00例：归一化的3阶巴特沃思低通滤波器为1Hro(s)=(s+1)(s?+s+1)3dB截频为wc的3阶巴特沃思低通滤波器为0H(s)=Ho(3)=s/ 0,(s+0)s?+0s+0)%归一低通到非归一低通的频率变换%确定归一低通N=3;Wc=2;[z,p,k]-buttap(N);[num,den]-zp2tf(z,p,k);%频率变换[numt,dent] = Ip2lp(num,den,Wc);

4.2 模拟频率变换 • 问题的提出 • 低通到低通的变换 • 低通到高通的变换 • 低通到带通的变换 • 低通到带阻的变换 问题的提出 如何设计模拟 高通 、带通、带阻滤波器? 4.2.1 低通到低通的变换 低通到低通的变换为 0 HLP (s) = HL (s)s = s/ 将 s = j ， s = j 代入 0 s = s/ 中得 0  = / 例：归一化的 3 阶巴特沃思低通滤波器为 ( 1)( 1) 1 ( ) 0 2 + + + = s s s H s L 3dB 截频为 wc 的 3 阶巴特沃思低通滤波器为 ( )( ) ( ) ( ) / 2 2 3 0 c c c c L L c s s s H s H s s s      + + + = = = %归一低通到非归一低通的频率变换 %确定归一低通 N=3;Wc=2; [z,p,k]=buttap(N); [num,den]=zp2tf(z,p,k); %频率变换 [numt,dent] = lp2lp(num,den,Wc);    p s 0 p 0s   =