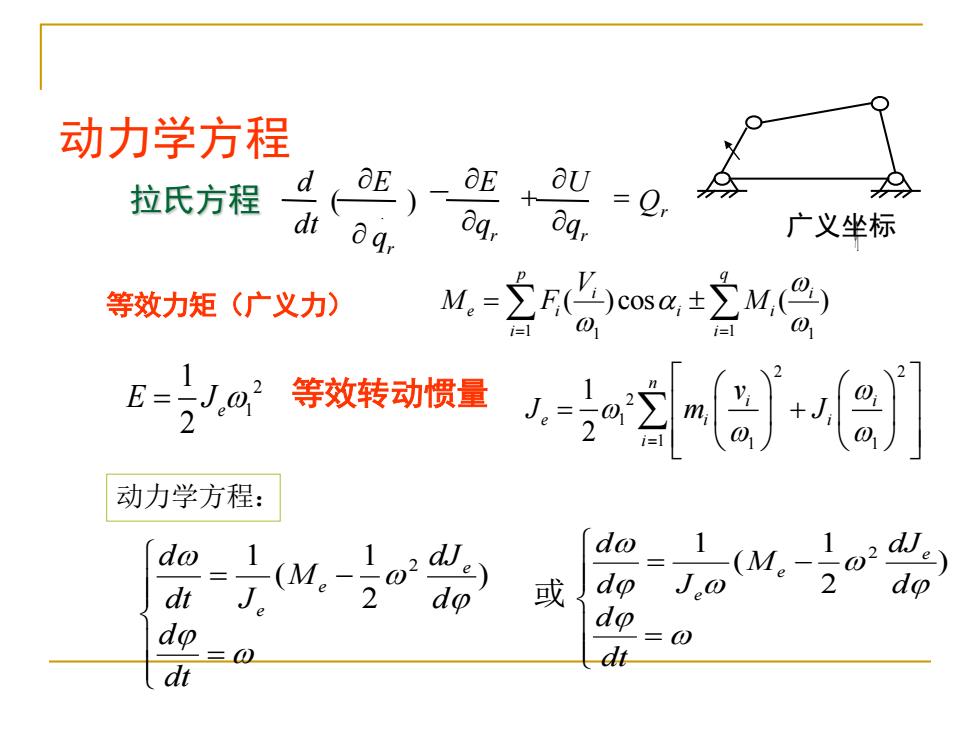
动力学方程 拉氏方程 OE+ U dt qr oqr 8q. 广义坐标 等效力矩(广义力) M。= i=1 E=- J02 等效转动惯量 J.2 2 动力学方程: 1 do 1 -(M -0 dt 或 do Jo 2 do do dt dt
动力学方程 2 1 1 2 E J = e = = − dt d d dJ M dt J d e e e ) 2 1 ( 1 2 动力学方程: 或 = = − dt d d dJ M d J d e e e ) 2 1 ( 1 2 等效力矩(广义力) = = = q i i i p i i i e i M V M F 1 1 1 1 ( ) cos ( ) 2 2 2 1 1 1 1 1 2 n i i e i i i v J m J = = + 等效转动惯量 Q q U q E q E dt d r r r r ( ) . = + - 拉氏方程 1 广义坐标

常见的动力学 转动构件为等效构件 方程类型 do -(M 2 dl -0 dt do 1.J。=常数 M。=常数 do 2J。=常数 M。=Me(9) dt 3. Je=常数 M-M(O 单自由度机械系统动力学微分 4. J。=J(φ) 方程的解法:取决于等效力 (矩)和等效转动惯量(等效 M。=M(o,p) 质量)的变化与否。 5 Je-Je( 解法:解析法和数值法 M。=Me(o,t)
常见的动力学 方程类型 = = − dt d d dJ M dt J d e e e ) 2 1 ( 1 2 1. Je =常数 Me= 常数 2 Je =常数 Me=Me( ) 3. Je =常数 M e=M ( ) 4. 5. () e e J = J (,) Me = Me Je=Je ( ) M M ( ,t) e = e 单自由度机械系统动力学微分 方程的解法:取决于等效力 (矩)和等效转动惯量(等效 质量)的变化与否。 解法:解析法和数值法 转动构件为等效构件
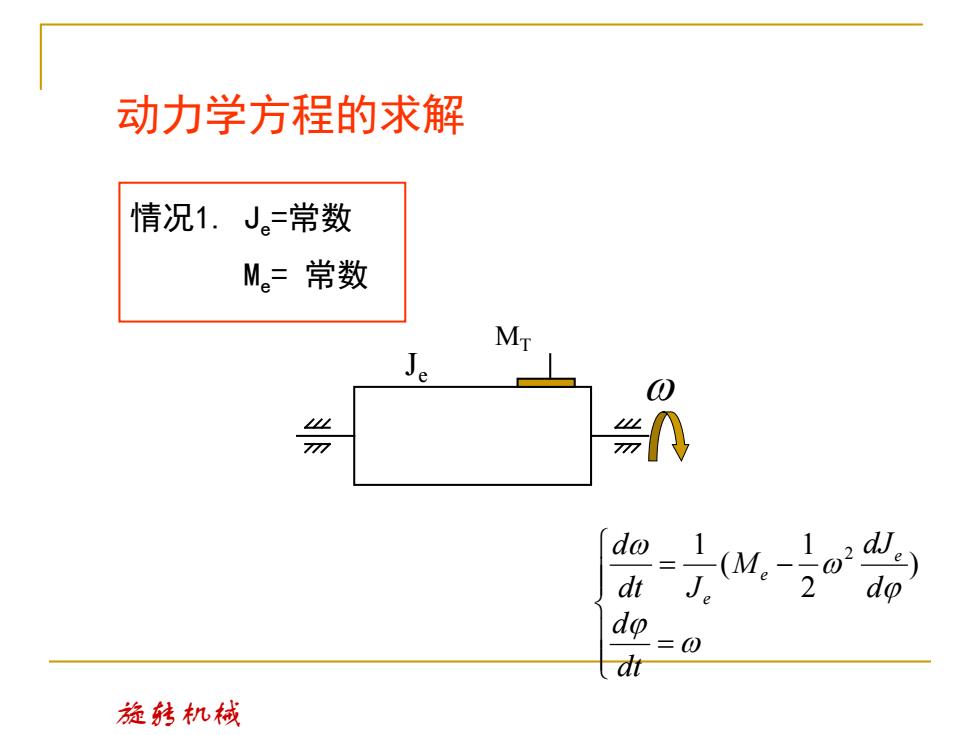
动力学方程的求解 情况1.J。=常数 M。=常数 do 1 (M。 12d 01 dt J。 2 do do =0 dt 旋转机械
情况1. Je =常数 Me= 常数 动力学方程的求解 MT Je 旋转机械 = = − dt d d dJ M dt J d e e e ) 2 1 ( 1 2
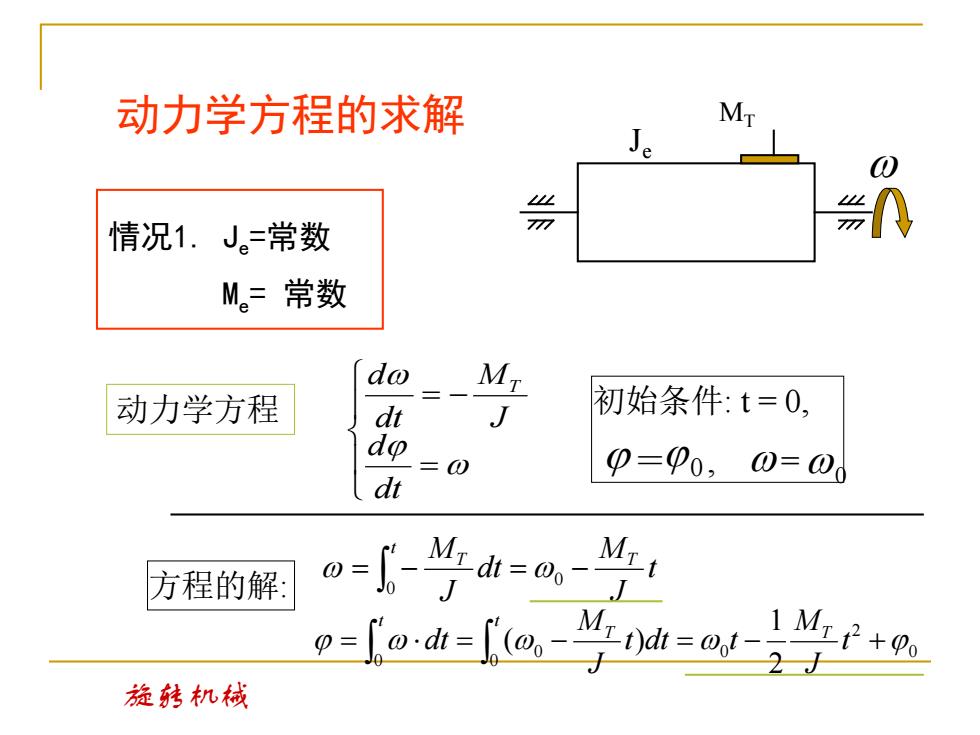
动力学方程的求解 情况1.J。=常数 M。常数 do MT 动力学方程 dt J 初始条件:t=0, o =0 p=p0,0=0 dt M红t 方程的解 1M红+9o 旋转机械
情况1. Je =常数 Me= 常数 动力学方程的求解 MT Je = = − dt d J M dt d T 动力学方程 t J M dt J M T t T = − = − 0 0 = = − = − + t T T t t J M t dt t J M dt 0 0 2 0 0 0 2 1 ( ) 方程的解: 初始条件: t = 0, = 0 , = 0 旋转机械
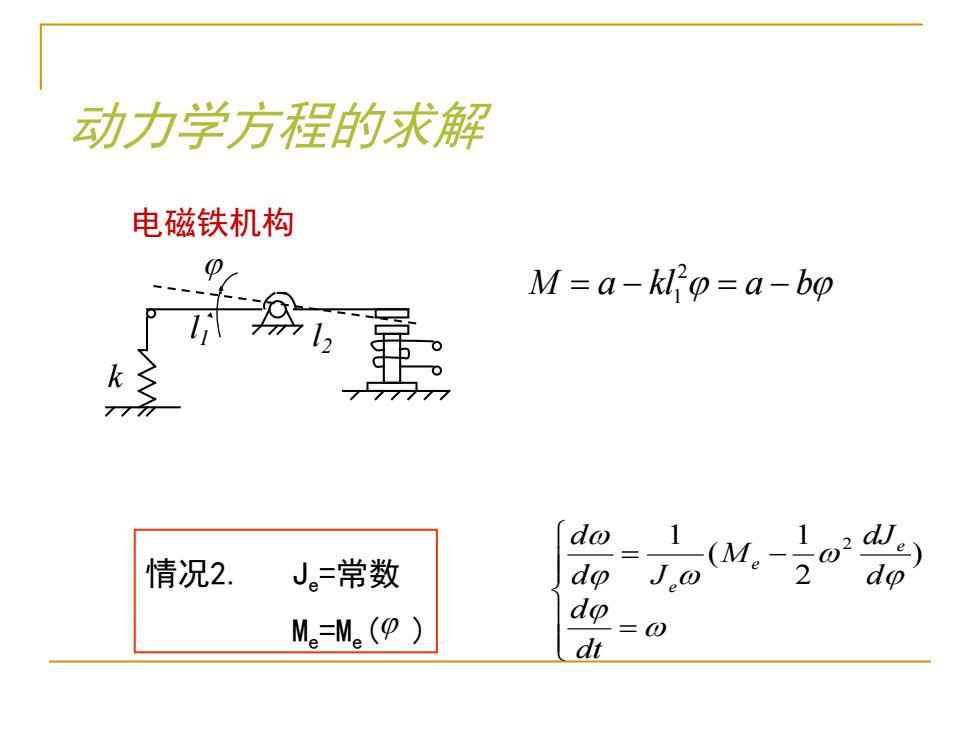
动力学方程的求解 电磁铁机构 M=a-kl'o=a-bo k do _1 情况2. J。常数 do J -(Me- M。=Me(9) do =0 dt
动力学方程的求解 情况2. Je =常数 Me=Me( ) k l1 l2 电磁铁机构 2 M a kl a b = − = − 1 = = − dt d d dJ M d J d e e e ) 2 1 ( 1 2