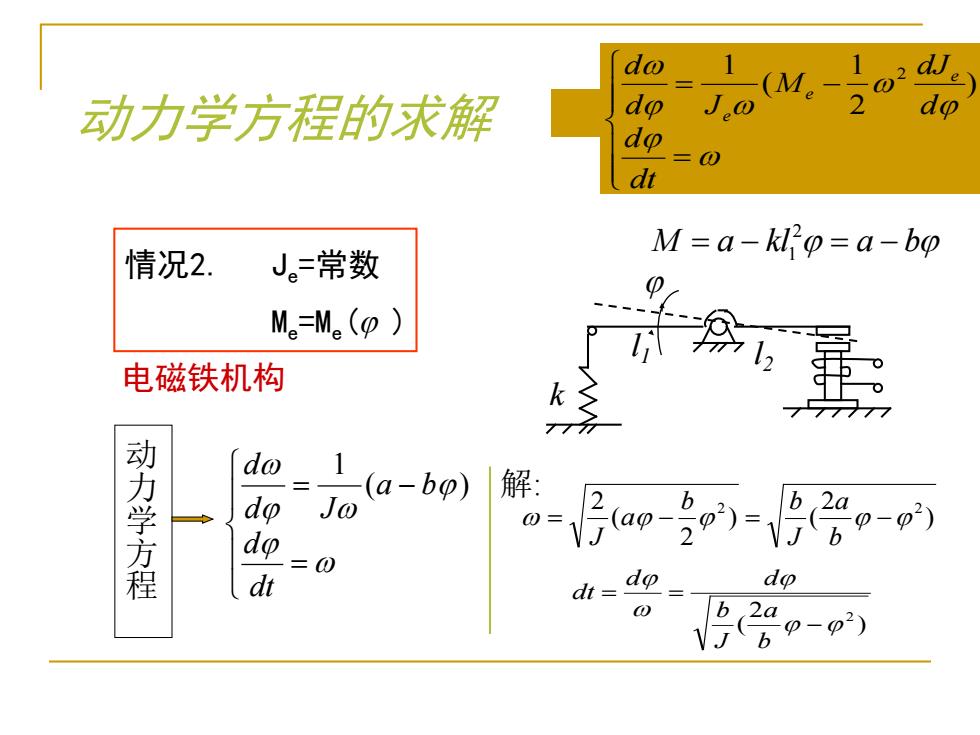
do (Me 0 动力学方程的求解 do J do =0 dt 情况2 J。常数 M=a-kl'o=a-bo Me=M( 电磁铁机构 k 动力学方程 dw 、1 (a-bp)解: dp Jo b 2a 0= do e- =0 dt dt do do b 2a p-p2)
动力学方程的求解 情况2. Je =常数 Me=Me( ) = = − dt d a b d J d ( ) 动 1 力 学 方 程 ) 2 ) ( 2 ( 2 2 2 = − = − b a J b b a J ) 2 ( 2 − = = b a J b d d dt 解: k l1 l2 电磁铁机构 2 M a kl a b = − = − 1 = = − dt d d dJ M d J d e e e ) 2 1 ( 1 2
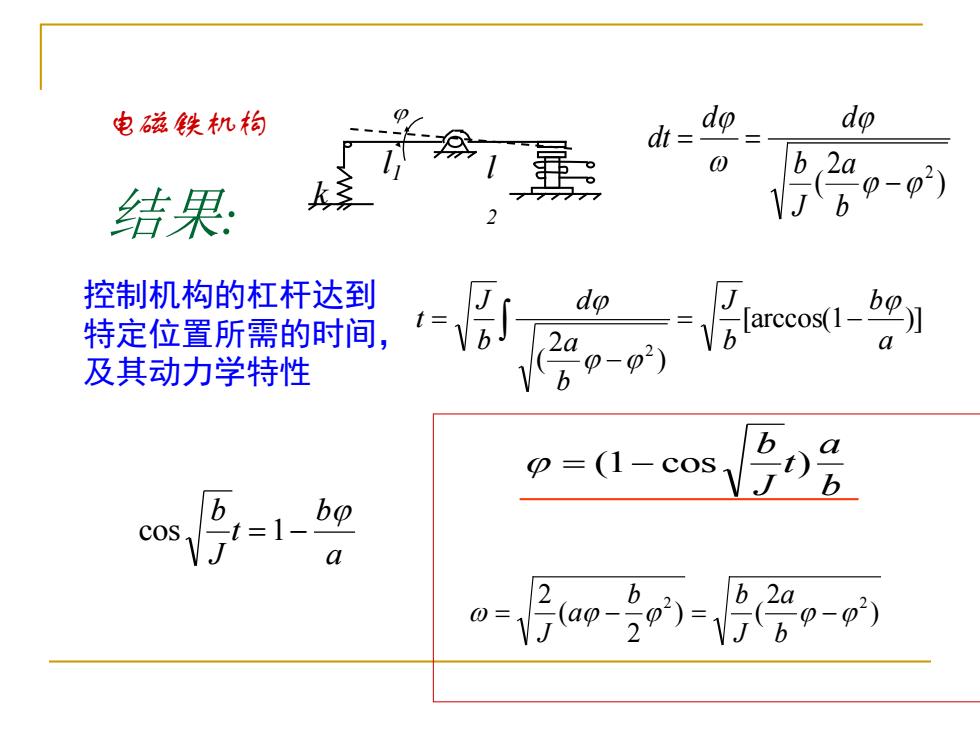
电磁铁机构 do dp 分1 dt= b 2a 结果 0-02) 控制机构的杠杆达到 dp 特定位置所需的时间, a 及其动力学特性 b =(1-cos b cos bp b b 2a 0=了 a0-207bp-0)
结果: [arccos(1 )] ) 2 ( 2 a b b J b a d b J t = − − = a b t J b cos = 1− b a t J b = (1− cos ) ) 2 ( 2 − = = b a J b d d dt ) 2 ) ( 2 ( 2 2 2 = − = − b a J b b a J 电磁铁机构 控制机构的杠杆达到 特定位置所需的时间, 及其动力学特性 k l1 l 2