复旦大学：《集成电路工程》教学资源（硕士士学位论文）基准源和温度检测模块设计

射频接收机中基准源和温度检测模块设计 /DD VBE Vss VREF=VBE+K△VBE AVBE K△VBE 图2-1带隙基准电压源基本原理图 下面对VBE的负温度系数和△VBE正温度系数进行分析。 (1)负温度系数电压VBE 图2-2NPN型BJT 下面通过公式推导来说明VBE的负温度系数特性。图2-2给出NPN型 BJT(Bipolar Junction Transistor),根据其拓扑结构，给出基极一发射极Vae与 集电极电流1c关系的公式： l。=-/sexp (2.8) 式中V=kTg,k为波尔兹曼常数。s是饱和电流，有以下表达式： 1s= AkTn2ū(T) (2.9) Na A为发射结面积，N杂质掺杂度。n为硅的本征载流子浓度，其与温度的关系可 表示为ox0L-V」 V.(T) 其中Vg()为硅的带隙电压，其随温度T变化， 可表达为Vg(刀=Vg0-aT,Vgo为0K时，硅的带隙电压，a为常数。币为基极中 少子平均迁移率，其与温度的关系可表示为(T)∝Tn,其中n≈3/2。综合以 上参数与温度的关系，可以得到s与温度的关系 Is ac T4-exp (2.10) V

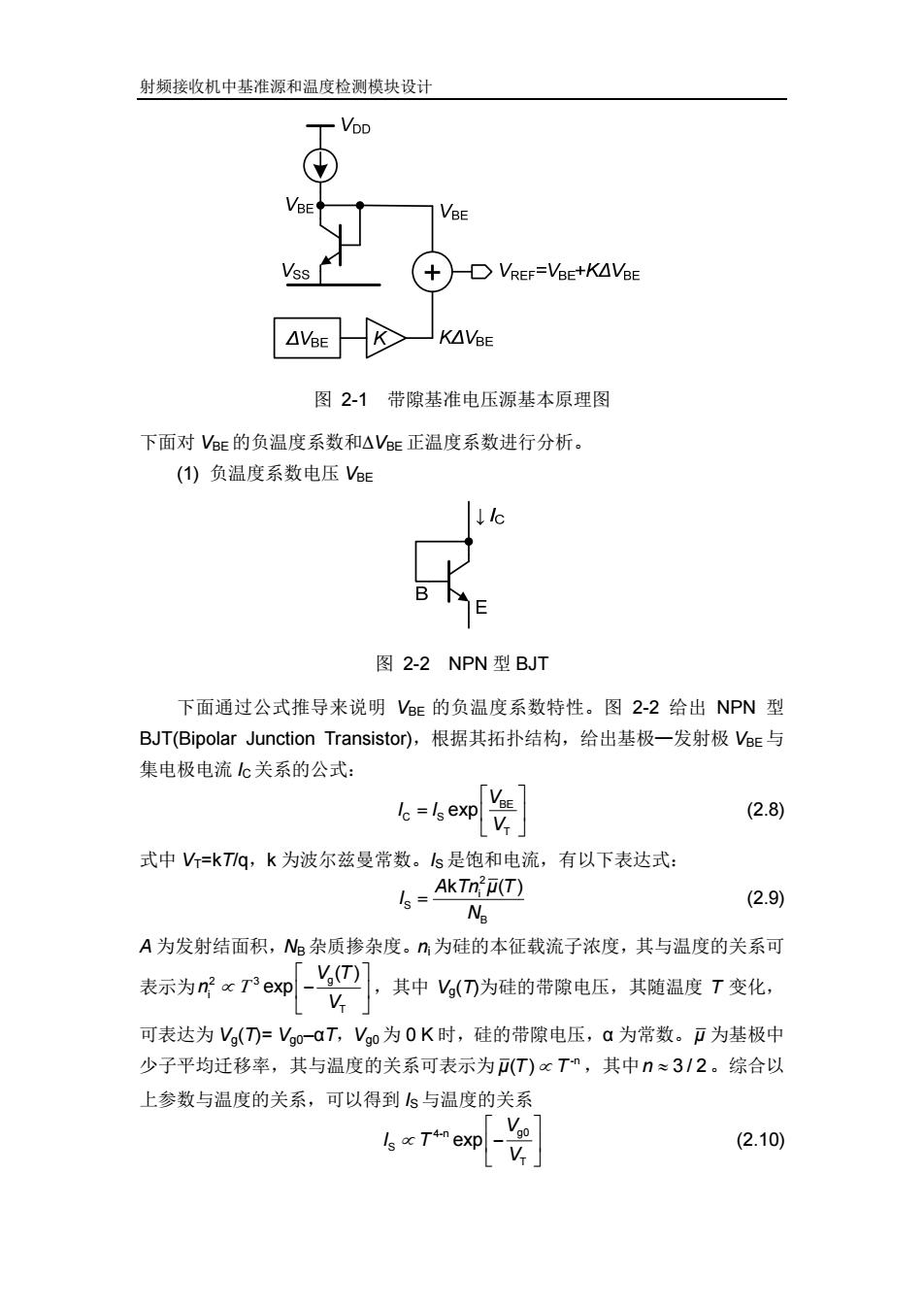
射频接收机中基准源和温度检测模块设计 图 2-1 带隙基准电压源基本原理图 下面对 VBE 的负温度系数和∆VBE 正温度系数进行分析。 (1) 负温度系数电压 VBE 图 2-2 NPN 型 BJT 下面通过公式推导来说明 VBE 的负温度系数特性。图 2-2 给出 NPN 型 BJT(Bipolar Junction Transistor)，根据其拓扑结构，给出基极—发射极 VBE与 集电极电流 IC关系的公式：        BE C S T exp V I I V (2.8) 式中 VT=kT/q，k 为波尔兹曼常数。IS是饱和电流，有以下表达式： 2 i S B A Tn k () μ T I N  (2.9) A 为发射结面积，NB 杂质掺杂度。ni 为硅的本征载流子浓度，其与温度的关系可 表示为          2 3 g i T ( ) exp V T n V ，其中 Vg(T)为硅的带隙电压，其随温度 T 变化， 可表达为 Vg(T)= Vg0–αT，Vg0为 0 K 时，硅的带隙电压，α 为常数。μ 为基极中 少子平均迁移率，其与温度的关系可表示为  -n μ( ) T T ，其中n  3/2。综合以 上参数与温度的关系，可以得到 IS与温度的关系        4-n g0 S T exp V I T V (2.10)

第二章带隙基准电压源电路设计 根据式(2.8)，先得到VE表达式： Vee =V In (2.11) 6 为得到VBE的温度系数，VBE对T求导 -学n+登- (2.12) 注意lc也与温度有关系，根据(2.10)表达的s关系，可以得到下式： OVeE Vo -(4-n)V,-Vao vol aT 入 (2.13) le aT 对上式做一个粗略估算，VE通常在0.7V,Vgo约为1.2V左右，n-3/2,(4-n) 大于0，所以上式第一项小于0。第二项通常与温度成阶乘关系，一般小于第一 项的绝对值，所以VE为负温度系数。 下面通过推导，给出VeE更为普遍的表达式。将式(2.10)带入式(2.8)，取 n=4-n,得到 lc(T)=CTn exp q(VBE(T)-Vgo) kT (2.14) 式中C为常数。对上式两边都求对数In,得到 n.(TI-hc-nnr-号Me)-y） (2.15) 取一参考温度T带入上式 m.l-hc-nhr=R是Me:)-。） (2.16) 将上述两式相减得到 (T) -nn7号.m-.-) (2.17) (T) 最后，整理可得VBE更为普遍的表达式： m--7+7+灯》-n (2.18) 从上式，可以清楚的看到，除了含有与T成一阶关系项，还包含刀T项，这也 表明，带隙基准源输出电压只能在一点取得零温度系数，要取得更低的温度系数， 就必须采用曲率补偿技术。 (2)正温度系数电压△VEB 13

第二章 带隙基准电压源电路设计 13 根据式(2.8)，先得到 VBE表达式：  C BE T S ln I V V I (2.11) 为得到 VBE 的温度系数，VBE对 T 求导            C S S C BE T C S T 2 SC S ln I I I I V V I I T T V T TI I I (2.12) 注意 IC也与温度有关系，根据(2.10)表达的 IS关系，可以得到下式：          BE T BE T g0 C C V V V VV (4 n) I T T IT (2.13) 对上式做一个粗略估算，VBE通常在 0.7 V，Vg0约为 1.2 V 左右，n≈3/2，(4–n) 大于 0，所以上式第一项小于 0。第二项通常与温度成阶乘关系，一般小于第一 项的绝对值，所以 VBE 为负温度系数。 下面通过推导，给出 VBE 更为普遍的表达式。将式(2.10)带入式(2.8)，取 η=4–n，得到 η BE g0 C q( ( ) ) ( ) exp k VT V I T CT T         (2.14) 式中 C 为常数。对上式两边都求对数 ln，得到 C BE g0 q ln[ ( )] lnC ηln ( ( ) ) k IT T V T V T    (2.15) 取一参考温度 Tr带入上式 C r r BE r g0 r q ln[ ( )] lnC ηln ( ( ) ) k IT T V T V T    (2.16) 将上述两式相减得到 C BE g0 BE r g0 Cr r r ( ) q q ln ηln ( ( ) ) ( ( ) ) () k k I T T VT V VT V IT T T T            (2.17) 最后，整理可得 VBE更为普遍的表达式： C BE g0 BE r r r Cr r k ( ) ( ) (1 ) ( ) ln ηln q () TT T T I T VT V VT T T IT T                 (2.18) 从上式，可以清楚的看到，除了含有与 T 成一阶关系项，还包含 TlnT 项，这也 表明，带隙基准源输出电压只能在一点取得零温度系数，要取得更低的温度系数， 就必须采用曲率补偿技术。 (2) 正温度系数电压∆VEB

射频接收机中基准源和温度检测模块设计 VEB /EB2 /EB1 Vss 图2-3正温度系数电压的产生 利用双极性三极管可以得到很精确的正温度系数电压。如图2-3所示，根据 式(2.11)的关系，可以得到△VEB为： AVee Venz Vea =V,In -V,InV In s (2.19) 1s2 1s1 如果图2-3中两个三极管的尺寸相同，则s1=s2,进一步可以得到： AVes =V In2st=V Inn (2.20) 由于V=kTq,可以看出AVEB是完美的正温度系数电压，仅包含一阶温度项。 透过上面对双极性晶体管来实现正负温度系数量方法的分析，只要通过对 VBE和△VEB适当组合，就可以得到一个零温度系数的输出电压，从而实现带隙基 准电压源。这里指的零温度系数电压并不是绝对的，由于VBE还存在高阶的负温 度系数成分，所以只能在某个点达到零温度系数，通常将这个点选在室温300K 下。图2-4给出了典型带隙基准电压源的温度系数，从图上可以看出VEF不是 只在某一点取得零温度系数，所以在低温度系数的应用，需要对VE中的高阶温 度项补偿，来得到更加趋于零温度系数的输出电压，因此，也将图2-4中的温 度系数的曲线成为一阶补偿的带隙基准电压源的温度曲线。 31 abel Vret VEB Temperature(K) 图2-4带隙基准电压源温度系数 最后，来说明如何在标准CMOS工艺下实现双极性晶体管。无疑，在集成

射频接收机中基准源和温度检测模块设计 图 2-3 正温度系数电压的产生 利用双极性三极管可以得到很精确的正温度系数电压。如图 2-3所示，根据 式(2.11)的关系，可以得到∆VEB为：    00 1 EB EB2 EB1 T T T S2 S1 S2 ∆ ln ln ln nI I nIS VV V V V V II I (2.19) 如果图 2-3 中两个三极管的尺寸相同，则 IS1= IS2，进一步可以得到：   1 EB T T S2 ∆ ln ln nIS V V Vn I (2.20) 由于 VT=kT/q，可以看出∆VEB是完美的正温度系数电压，仅包含一阶温度项。 透过上面对双极性晶体管来实现正负温度系数量方法的分析，只要通过对 VBE和∆VEB 适当组合，就可以得到一个零温度系数的输出电压，从而实现带隙基 准电压源。这里指的零温度系数电压并不是绝对的，由于 VBE还存在高阶的负温 度系数成分，所以只能在某个点达到零温度系数，通常将这个点选在室温 300K 下。图 2-4 给出了典型带隙基准电压源的温度系数，从图上可以看出 VREF不是 只在某一点取得零温度系数，所以在低温度系数的应用，需要对 VBE 中的高阶温 度项补偿，来得到更加趋于零温度系数的输出电压，因此，也将图 2-4 中的温 度系数的曲线成为一阶补偿的带隙基准电压源的温度曲线。 ∆VEB 图 2-4 带隙基准电压源温度系数 最后，来说明如何在标准 CMOS 工艺下实现双极性晶体管。无疑，在集成

第二章带隙基准电压源电路设计 电路设计，MOSFET管几乎替代了BJT,BJT仅在一些特殊应用场合使用，例 如高频。如果不能在标准CMOS工艺实现BJT,这就意味着增加成本，这显然 是很难接受。幸运的是，可以在n阱的CMOS工艺实现PNP型双极性晶体管， 如图25所示。p型衬底是集电区，但衬底必须接到电路的最负电源上。因此标 准CMOS工艺上的PNP管有一定的实现限制，这在设计过程中必须注意。 E n n阱 p型衬底 图2-5CMOS工艺中pnp双极性晶体管的实现 2.2电路结构及性能分析 本文一共设计了两个带隙基准电压源，一个是工作在2.1~3.3V电源电压下， 另一个工作在1.8V电源电压下。两者采用相同的结构。带隙基准电压源除了提 供输出参考电压，还提供PTAT电流。并且通过两个带隙基准的配合来实现芯片 全局供电方案，这将在2.4节进行介绍。 2.2.1电路结构 图2-6给出了带隙基准电压源的原理图。运放将节点1和节点2嵌至同一 电位，有V=V2。因此有 2=3-V2 R 其中Q2管为N个相同尺寸的PNP管的并联，因此流过每个PNP管的电流要 除以N,根据式(2.11)有 Ve82 V In NIs 由于Q3和Q2在单个晶体管的尺寸相同，因此。相同，因此可得 V In NA h2-R,2 (2.21) 该电流为PTAT电流，可用于输出，实现了电路的正温度系数部分。再通过电流 镜复制给第三路，因此得到输出参考电压的表达式为： 15

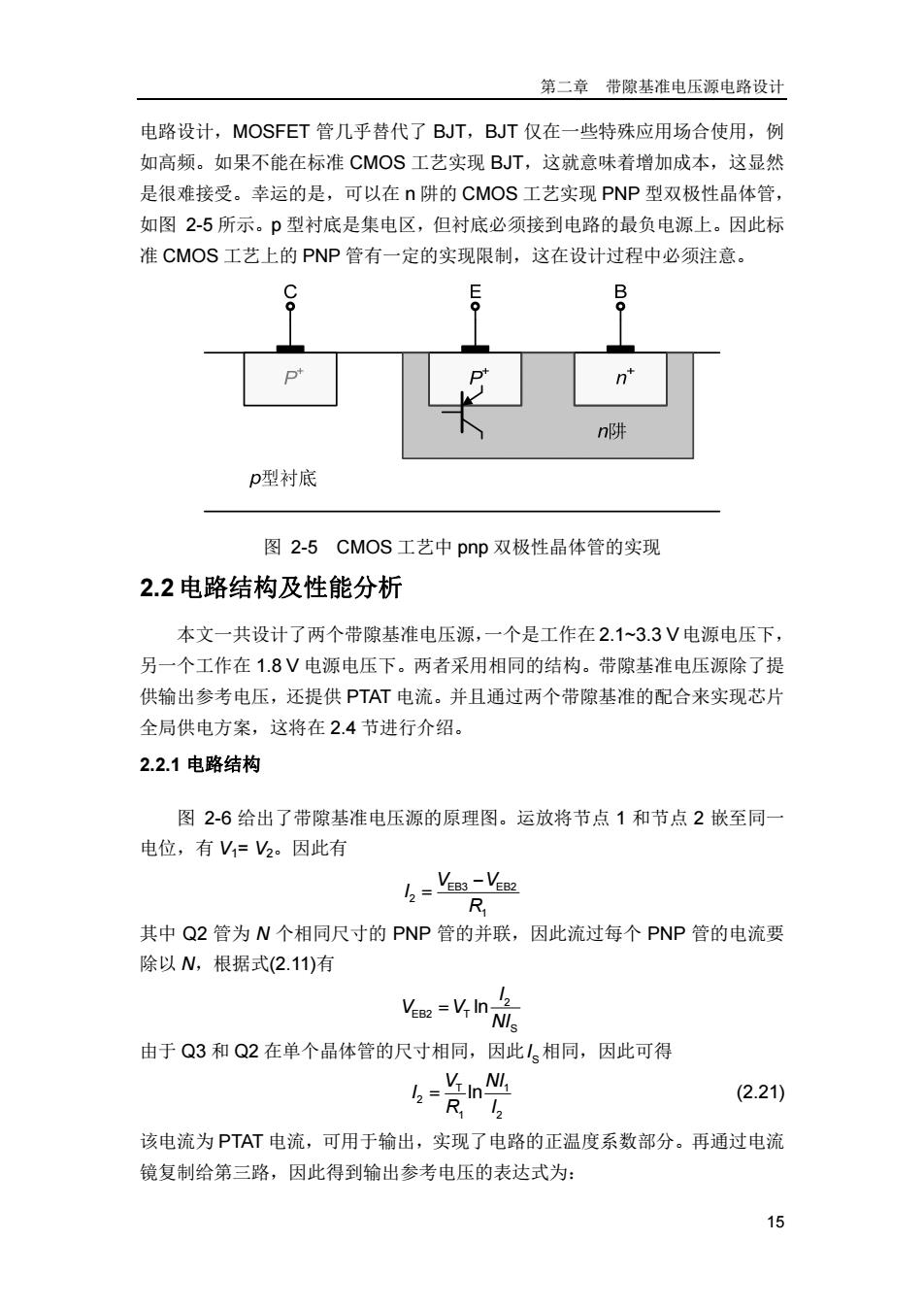
第二章 带隙基准电压源电路设计 15 电路设计，MOSFET 管几乎替代了 BJT，BJT 仅在一些特殊应用场合使用，例 如高频。如果不能在标准 CMOS 工艺实现 BJT，这就意味着增加成本，这显然 是很难接受。幸运的是，可以在 n 阱的 CMOS 工艺实现 PNP 型双极性晶体管， 如图 2-5 所示。p 型衬底是集电区，但衬底必须接到电路的最负电源上。因此标 准 CMOS 工艺上的 PNP 管有一定的实现限制，这在设计过程中必须注意。 图 2-5 CMOS 工艺中 pnp 双极性晶体管的实现 2.2 电路结构及性能分析 本文一共设计了两个带隙基准电压源，一个是工作在 2.1~3.3 V 电源电压下， 另一个工作在 1.8 V 电源电压下。两者采用相同的结构。带隙基准电压源除了提 供输出参考电压，还提供 PTAT 电流。并且通过两个带隙基准的配合来实现芯片 全局供电方案，这将在 2.4 节进行介绍。 2.2.1 电路结构 图 2-6 给出了带隙基准电压源的原理图。运放将节点 1 和节点 2 嵌至同一 电位，有 V1= V2。因此有   EB3 EB2 2 1 V V I R 其中 Q2 管为 N 个相同尺寸的 PNP 管的并联，因此流过每个 PNP 管的电流要 除以 N，根据式(2.11)有  2 EB2 T S ln I V V NI 由于 Q3 和 Q2 在单个晶体管的尺寸相同，因此 SI 相同，因此可得  T 1 2 1 2 ln V NI I R I (2.21) 该电流为 PTAT 电流，可用于输出，实现了电路的正温度系数部分。再通过电流 镜复制给第三路，因此得到输出参考电压的表达式为：

射频接收机中基准源和温度检测模块设计 VREF VEB1+ R2V-In 。Nl (2.22) 2 通过上面表达式，可以看出本电路并未使用曲率补偿技术，是最基本的一阶补偿。 VDD 2 O VREF 11J 2↓R ↓交R2 Ao 3 Co Vss 图2-6带隙基准电压源电路原理图 根据允许的电源电压的范围，采用了共源共栅电流镜结构来提高复制电流的 准确度。另一方面，由于本电路用于射频接收机中，对输出噪声要求十分严格。 为了取得在简单结构上，对噪声的最大优化，Q2管的N取值达到100以上。取 值如此之大，PNP管的不匹配必然给输出参考电压带来较大误差，必须对电路 进行修正。修正有软修正和硬修正两种，硬修正的成本较高，因此这里采用了软 修正的方法，通过数字信号控制Q2管的数目N,其电路实现方式如图2-7所示。 数字控制信号为3位，其通过3-8译码器产生S1~S7七个控制信号，控制由PNP 管和反相器组成的基本单元。基本单元中，反相器输入端连接控制信号，输出端 连接到PNP管的基极。以S1控制信号为例，当S1为低电平时，PNP基极电 压为VbD,PNP管关断不工作，相反，当S1为高电平时，PNP基极电压为GND, 与二极管连接的PNP管一样，PNP管正常工作。这样实现了数字信号控制PNP 导通数目N的要求。由于这样方法得到的PNP管基极电压未必一定偏置在GND, 但这种非理想因素带来的误差是几乎可以忽略的。该控制模块，可实现8个PNP 管数目的状态，步长为11，控制范围为109~186，在这个控制范围内，总能找 到一个合理的控制码ABC满足要求的温度系数，达到软修正的效果。这种方法

射频接收机中基准源和温度检测模块设计   2 1 REF EB1 T 1 2 ln R NI VV V R I (2.22) 通过上面表达式，可以看出本电路并未使用曲率补偿技术，是最基本的一阶补偿。 图 2-6 带隙基准电压源电路原理图 根据允许的电源电压的范围，采用了共源共栅电流镜结构来提高复制电流的 准确度。另一方面，由于本电路用于射频接收机中，对输出噪声要求十分严格。 为了取得在简单结构上，对噪声的最大优化，Q2 管的 N 取值达到 100 以上。取 值如此之大，PNP 管的不匹配必然给输出参考电压带来较大误差，必须对电路 进行修正。修正有软修正和硬修正两种，硬修正的成本较高，因此这里采用了软 修正的方法，通过数字信号控制Q2管的数目N，其电路实现方式如图 2-7所示。 数字控制信号为 3 位，其通过 3-8 译码器产生 S1~S7 七个控制信号，控制由 PNP 管和反相器组成的基本单元。基本单元中，反相器输入端连接控制信号，输出端 连接到 PNP 管的基极。以 S1 控制信号为例，当 S1 为低电平时，PNP 基极电 压为 VDD，PNP 管关断不工作，相反，当 S1 为高电平时，PNP 基极电压为 GND， 与二极管连接的 PNP 管一样，PNP 管正常工作。这样实现了数字信号控制 PNP 导通数目N的要求。由于这样方法得到的PNP管基极电压未必一定偏置在GND， 但这种非理想因素带来的误差是几乎可以忽略的。该控制模块，可实现 8 个 PNP 管数目的状态，步长为 11，控制范围为 109 ~186，在这个控制范围内，总能找 到一个合理的控制码 ABC 满足要求的温度系数，达到软修正的效果。这种方法