
4.2相量法的基本概念 正弦量与相量 例1.已知 i=100W2c0s314t+30°)A 解:i=100∠30°A u=220W2c0s(314t-60°)V j=220∠-60°V 试用相量表示i,u。 例2. 解: 己知1=50∠15°A,f=50Hz.i=50W2c0s(314t+15°)A 试写出电流的瞬时值表达式
例1.已知 试用相量表示 i , u 。 22 0 2 co s(3 1 4 t 6 0 ) V 100 2 co s(314 3 0 )A o o = − = + u i t 解: 220 6 0 V 100 3 0 A o o = − = • • U I 例2. 试写出电流的瞬时值表达式。 解: 5 0 2 c o s (314 1 5 ) A 5 0 1 5 A , 5 0 H z . i = t + = = • I f 已 知 4.2 相量法的基本概念 一、正弦量与相量
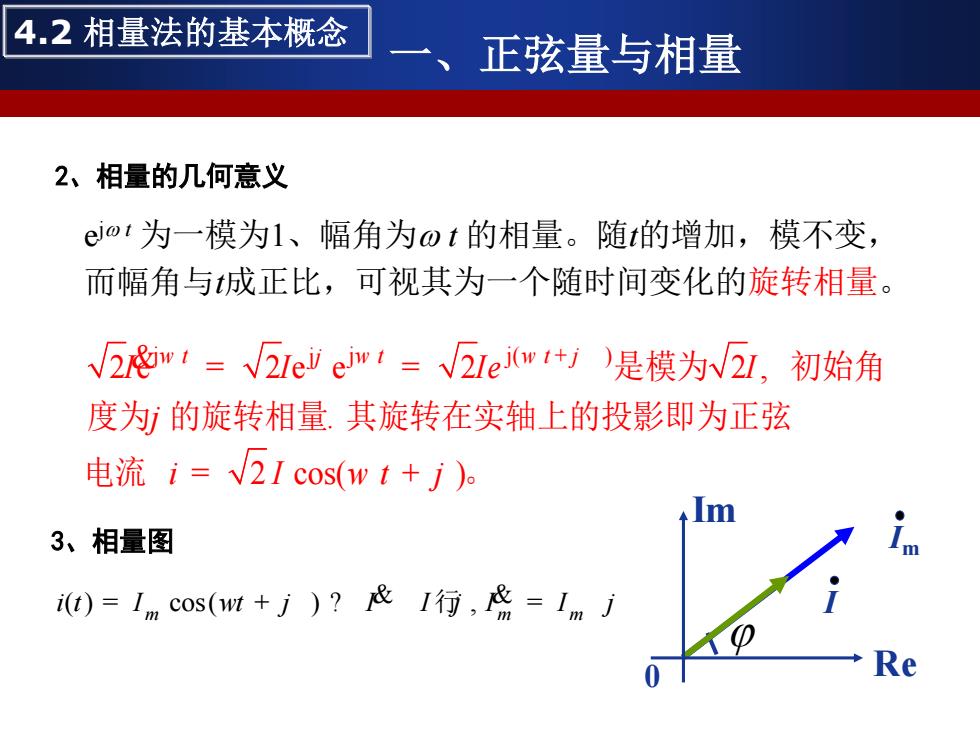
4.2相量法的基本概念 正弦量与相量 2、相量的几何意义 eot为一模为1、幅角为ot的相量。随t的增加,模不变, 而幅角与成正比,可视其为一个随时间变化的旋转相量。 √2w1=√2leew1=√2 lej(w/)是模为N2L,初始角 度为ⅵ的旋转相量.其旋转在实轴上的投影即为正弦 电流i=√2Icos(wt+j)。 3、相量图 m i)=1mcos(M+j)?&I行,&=1mj Re
2、相量的几何意义 e jw t 为一模为1、幅角为w t 的相量。随t的增加,模不变, 而幅角与t成正比,可视其为一个随时间变化的旋转相量。 j j j( ) j 2 e 2 e e 2 2 , . 2 cos( ) t t t I I Ie I i I t w w w j j j w j + = = = + & 是模为 初始角 度为 的旋转相量 其旋转在实轴上的投影即为正弦 电流 。 4.2 相量法的基本概念 一、正弦量与相量 3、相量图 ( ) cos( ) , m m m i t I t I = + = w j j j ? I I & & I行 Im Re 0 Im I

4.2相量法的基本概念 二、 正弦量的相量运算 1、同频率正弦量相加减 u(t)=2Ucos(@t+)=Re(v2Uei') u2(t)=√2U2cos(ot+p2)=Re(√2j2eJo') 复数运算u()=4,()+u,()=Re(V2j1eo)+Re(√2jeo) Re=Re()=Re(v2+U2)ei) 可得其相量关条为:0=U,+U, 相量运算 W1±W2=3 将三角函数运算转化为相量运算 运算法则:与复数相同! &?咚 (1)直角坐标实部虚部加减 (2)极坐标相量图平行四边形法则
1、 同频率正弦量相加减 将三角函数运算转化为相量运算 运算法则:与复数相同! (1)直角坐标实部虚部加减 (2)极坐标相量图平行四边形法则 ( ) 2 cos( ) R e( 2 e ) ( ) 2 cos( ) R e( 2 e ) j 2 2 2 2 j 1 1 1 1 t t u t U t U u t U t U w w w w • • = + = = + = R e( 2 e 2 e ) R e( 2 ( ) e ) ( ) ( ) ( ) R e( 2 e ) R e( 2 e ) j 1 2 j 2 j 1 j 2 j 1 1 2 t t t t t U U U U u t u t u t U U w w w w w • • • • • • = + = + = + = + U U U 1 U 2 可得其相量关系为: = + u1 u2 = u3 U U U 1 2 3 & & & ? Re[ 2 e ] j t U& w 4.2 相量法的基本概念 二、正弦量的相量运算 复数运算 相量运算