
导航 3.做一做:若平面a内的任何直线都平行于平面B,则α与的位 置关系是 答案:a∥B
导航 3.做一做:若平面α内的任何直线都平行于平面β,则α与β的位 置关系是 . 答案:α∥β

导航 二、平面与平面平行的判定定理 【问题思考】 1.若平面a内有无数条直线都与平面平行,侧a与B平行吗? 提示:不一定
导航 二、平面与平面平行的判定定理 【问题思考】 1.若平面α内有无数条直线都与平面β平行,则α与β平行吗? 提示:不一定

2.填空:平面与平面平行的判定定理 ()文字语言:如果一个平面内有两条 直线分别平行于另 一个平面,那么这两个平面平行. (2)符号语言:如果lca,mca,ln呋0,l∥B,m∥B,那么a∥B. (3)图形表示:如图所示 m P 推论:如果一个平面内有两条 直线分别 平行于另一个平面内的 直线,那么这两 个平面平行
导航 2.填空:平面与平面平行的判定定理 (1)文字语言:如果一个平面内有两条相交直线分别平行于另 一个平面,那么这两个平面平行. (2)符号语言:如果l⊂α,m⊂α,l∩m≠⌀ ,l∥β,m∥β,那么α∥β. (3)图形表示:如图所示. 推论:如果一个平面内有两条相交直线分别 平行于另一个平面内的两条直线,那么这两 个平面平行
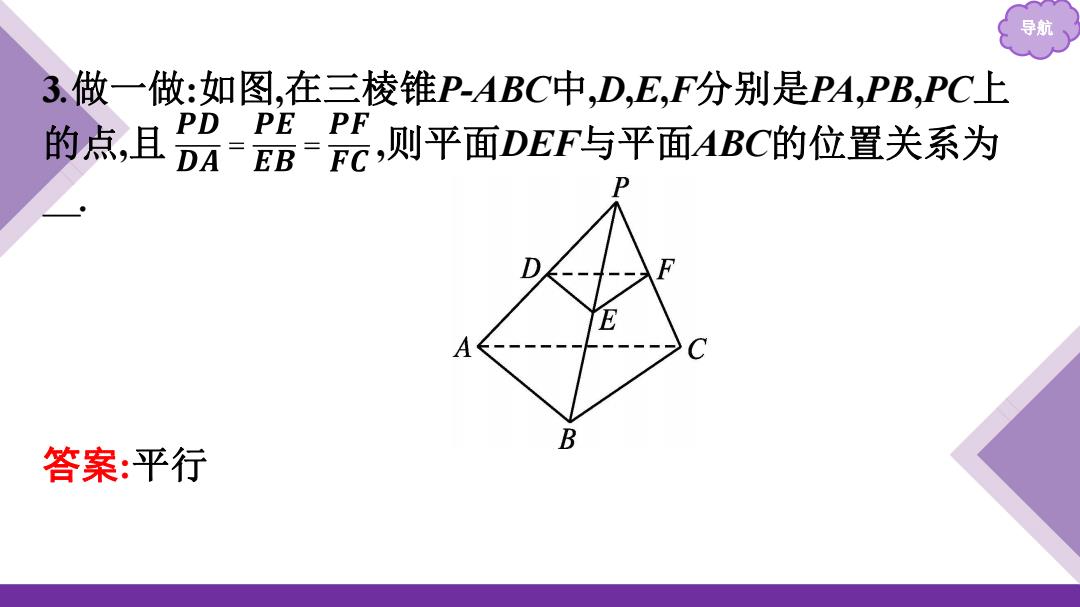
导航 3.做一做:如图,在三棱锥P-ABC中,D,E,F分别是PA,PB,PC上 的点,且册BC,则平面DEF与平面4BC的位置关系为 C B 答案:平行
导航 3.做一做:如图,在三棱锥P-ABC中,D,E,F分别是PA,PB,PC上 的点,且 ,则平面DEF与平面ABC的位置关系为 . 答案:平行

导月 三、平面与平面平行的性质定理 【问题思考】 L.若平面a∥平面B,直线mca,直线ncB,则m与n的位置关系是 什么? 提示:平行或异面. 2.已知平面a∥平面B,直线lca,如何在平面B内作出一条直线, 使a∥? 提示:过1作一平面%,设y∩B=,则a∥1
导航 三、平面与平面平行的性质定理 【问题思考】 1.若平面α∥平面β,直线m⊂α,直线n⊂β,则m与n的位置关系是 什么? 提示:平行或异面. 2.已知平面α∥平面β,直线l⊂α,如何在平面β内作出一条直线a, 使a∥l? 提示:过l作一平面γ,设γ∩β=a,则a∥l