
第二讲 洛必达法则
第二讲 洛必达法则

洛必达法则 一、洛必达法则 二、其它未定型的处理 三、理论应用
洛必达法则 一、洛必达法则 二、其它未定型的处理 三、理论应用

洛必达法则 一、洛必达法则 二、其它未定型的处理 三、理论应用
洛必达法则 一、洛必达法则 二、其它未定型的处理 三、理论应用

洛必达法则 情形不的洛必达法则 > 一情形下的洛必达法则 (1)lim f(x)=lim F(x)=0 (1)lim f(x)=lim F(x)=co x-0 x->a (2)在点a的某去心邻域内, (2)当|x>N时,f'(x,F(x) f'(x),F'(x)存在且F'(x)≠0 存在且F'(x)≠0 ③)im f(x) 在(或为o) (3)lim f'(x) aF'(x) 存在(或为∞) x→aF'(x) 则 lim =lim f'(x) 则 limf)=lim) x→aF(x →aF'(x) a F(x) x→aF'(x) ●注 在相应的条件下,对其它过程也成立
一、洛必达法则 若 ➢ 情形下的洛必达法则 0 0 lim ( ) = lim ( ) = 0 → → f x F x x a x a (1) (2) (3) 则 ( ) ( ) lim lim ( ) ( ) x a x a f x f x → → F x F x = 情形下的洛必达法则 ➢ f (x), F(x) 存在,且 F(x) 0 在点a的某去心邻域内, ( ) ( ) lim F x f x x a → 存在(或为 ) 若 = = → → lim f (x) lim F(x) x a x a (1) (2) (3) 则 ( ) ( ) lim lim ( ) ( ) x a x a f x f x → → F x F x = ( ) ( ) lim F x f x x a → 存在(或为 ) 且 F(x) 0 f (x), F(x) 存在, 当 | x | N 时, ⚫注 在相应的条件下,对其它过程也成立
一、洛必达法则 >应用举例 ◆例1 x-sInx lim ◆例2 Inx lim- x>0 x→1x-1 ◆例3 lim (1+x)2-1 sinx ◆例4 lim x>0 x x→0元 arctan 2 π sInx arctanx ◆例5 lim 2 x→0 π 1 ◆例6 lim -arctan- X>+0 2 X Inx ◆例7 lim ◆例8 lim Ax (2>0) X-→+00 x->+0
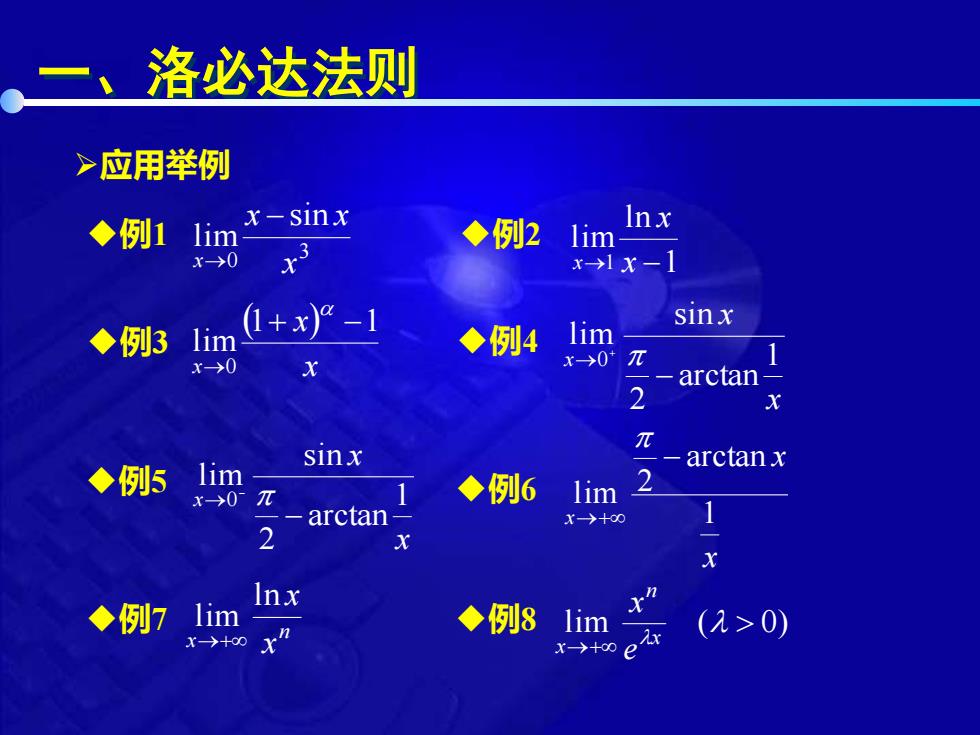
一、洛必达法则 ➢应用举例 ◆例1 3 0 sin lim x x x x − → ◆例2 1 ln lim →1 x − x x ◆例3 ( ) x x x 1 1 lim 0 + − → ◆例4 x x x 1 arctan 2 sin lim 0 − → + ◆例5 x x x 1 arctan 2 sin lim 0 − → − ◆例6 x x x 1 arctan 2 lim − →+ ◆例7 n x x ln x lim →+ ◆例8 lim ( 0) →+ x n x e x