
第三讲 泰勒公式
第三讲 泰勒公式

泰勒公式 一、泰勒公式 二、几个初等函数的麦克劳林公式 三、泰勒公式的应用
泰勒公式 一、泰勒公式 二、几个初等函数的麦克劳林公式 三、泰勒公式的应用

泰勒公式 一、泰勒公式 二、几个初等函数的麦克劳林公式 三、泰勒公式的应用
泰勒公式 一、泰勒公式 二、几个初等函数的麦克劳林公式 三、泰勒公式的应用
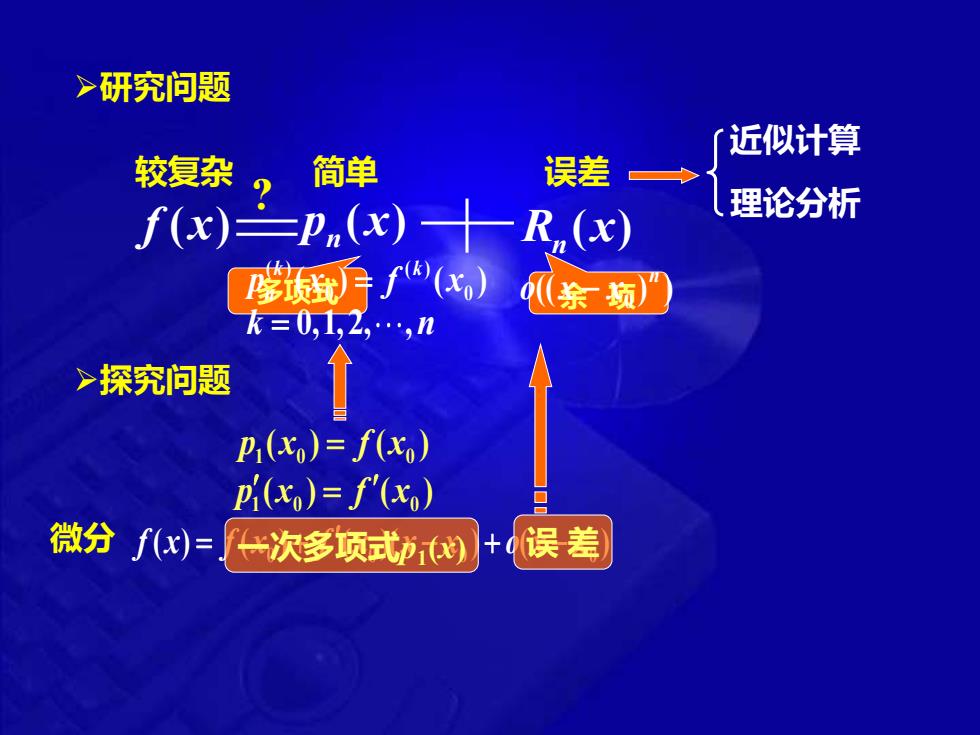
>研究问题 近似计算 较复杂 简单 误差 f(x)二P(x)十R.(x) 理论分析 学逅手f(x) k三01,Z,.,n >探究问题 ↑ Pi(x)=f(xo) P1(x)=f'(x) 微分fx)=÷次多项式间+误差)
➢研究问题 f (x) 多项式 余 项 p (x) n R (x) n 较复杂 简单 误差 近似计算 理论分析 微分 ( ) ( ) ( )( ) ( ) 0 0 0 0 f x = f x + f x x − x + o x − x ( ) ( ) 1 0 0 p x = f x ( ) ( ) 1 0 0 p x = f x ( ) ( ) 0 ( ) 0 ( ) p x f x k k n = k n = 0,1,2, , (( ) ) 0 n o x − x ? 一次多项式p1 (x) 误 差 ➢探究问题

>Pn(x)的确定 Pa(x)=ao+aj(x-xo)+az(x-xo)2++a(x-xo)" 令x→x→an=p(x)=f(x) P(x)=aj+2a2(x-xo)++na (x-xo)" 令r→一a,=%()-x》 =2a++mn-1a.c- 1 令x→x一4,=)=" 2! 2! p(x)=n 令→6一4,=p2)“《) n! n 2! f((x-x n
令 ( ) a0 = p x0 令 1! ( ) 0 1 p x a n = 令 2! ( ) 0 2 p x a n = 令 ! ( ) 0 ( ) n p x a n n n = ( ) x0 = f 1! ( ) x0 f = 2! ( ) 0 f x = ! ( ) 0 ( ) n f x n = ➢ pn (x)的确定