
第一讲 微分中值定理
第一讲 微分中值定理

微分中值定理 一、罗尔定理 二、 拉格朗日中值定理 三、柯西中值定理 四、中值定理的应用
微分中值定理 一、罗尔定理 二、拉格朗日中值定理 三、柯西中值定理 四、中值定理的应用

微分中值定理 罗尔定理 二、 拉格朗日中值定理 三、柯西中值定理 四、中值定理的应用
微分中值定理 一、罗尔定理 二、拉格朗日中值定理 三、柯西中值定理 四、中值定理的应用
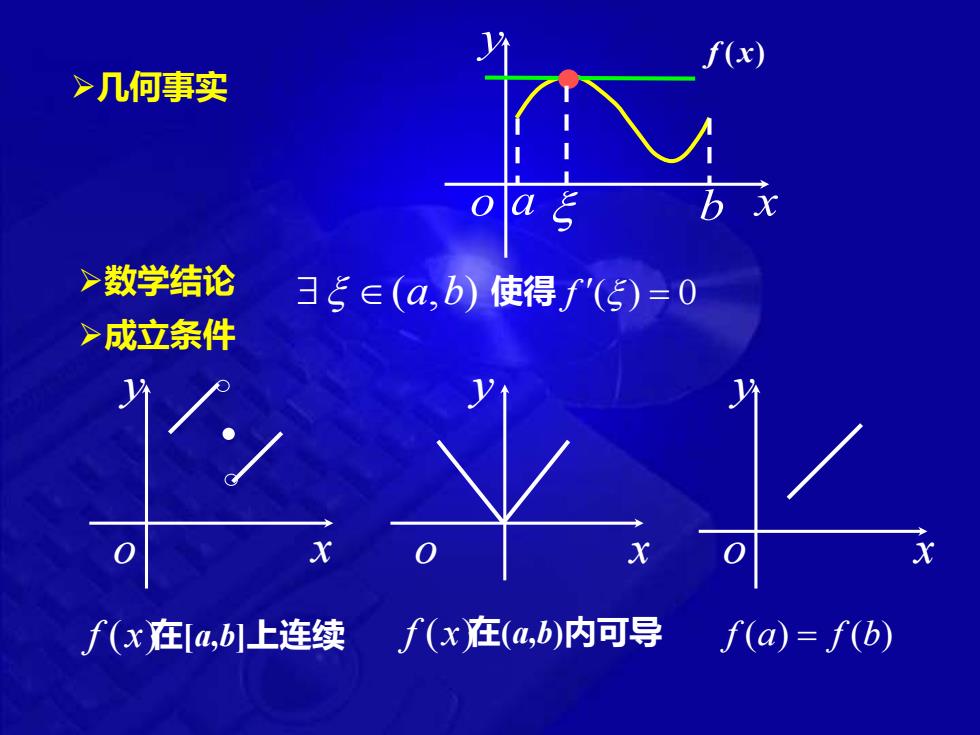
>几何事实 >数学结论 3飞∈(a,b)使得f'(5)=0 >成立条件 f(x在a,b]上连续 f(x在(a,b)内可导 f(a)=f(b)
➢几何事实 x y o a b (a,b) 使得 f () = 0 f (x) 在[a,b]上连续 f (x) 在(a,b)内可导 f (a) = f (b) x y o x y o x y o ➢数学结论 ➢成立条件 f (x)
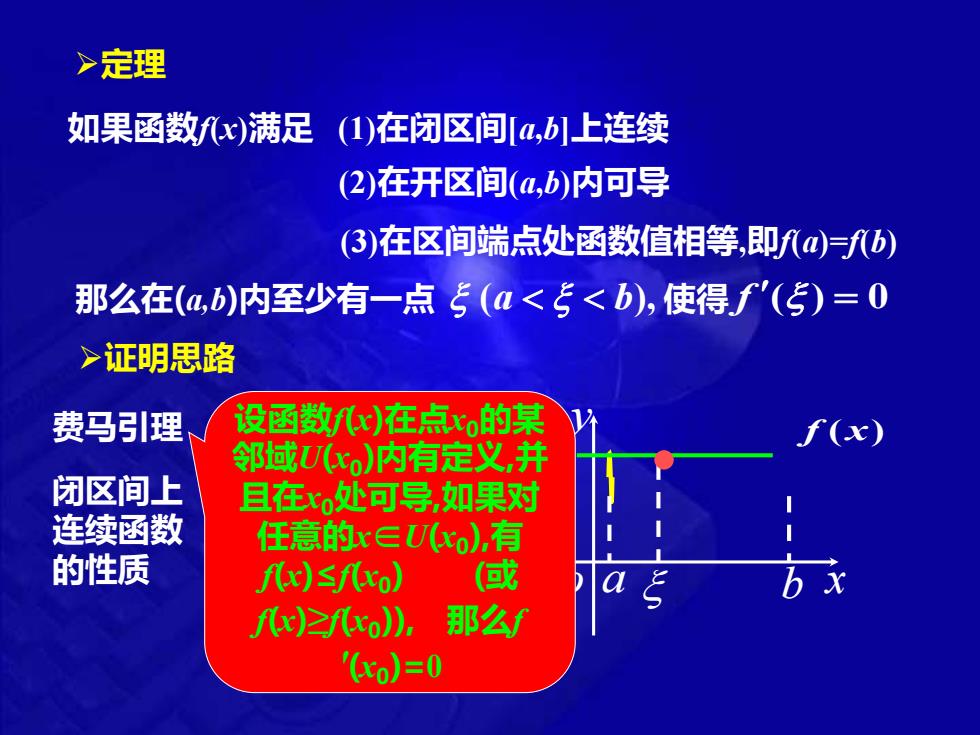
>定理 如果函数x)满足 (1)在闭区间a,b1上连续 (2)在开区间(a,b)内可导 (3)在区间端点处函数值相等,即fa)=fb) 那么在(4,b)内至少有一点5(a<5<b),使得f'(5)=0 >证明思略 费马引理 设函数/y)在点xo的某 (x) 邻域Uo)内有定义,井 闭区间上 且在x。处可导,如果对 连续函数 任意的r∈Uo),有 的性质 fx)sf八xo) (回或 fw)≥o),那么 xo)=0
x y o a b f (x) 如果函数f(x)满足 ➢定理 (1)在闭区间[a,b]上连续 (2)在开区间(a,b)内可导 (3)在区间端点处函数值相等,即f(a)=f(b) 那么在(a,b)内至少有一点 ( ), a b 使得 f ( ) 0 = ➢证明思路 费马引理 设函数f(x)在点x0的某 邻域U(x0 )内有定义,并 且在x0处可导,如果对 任意的x∈U(x0 ),有 f(x)≤f(x0 ) (或 f(x)≥f(x0 )), 那么f '(x0 )=0 闭区间上 连续函数 的性质