核心重难探究 知识点一对角线互相垂直的平行四边形是菱形 【例1】如图,在Rt△ABC中,∠B=90°,点E是AC的中点, AC=2AB,∠BAC的平分线AD交BC于点D,作AF∥BC,连接DE 并延长交AF于点F,连接FC E 求证:四边形ADCF是菱形 A B
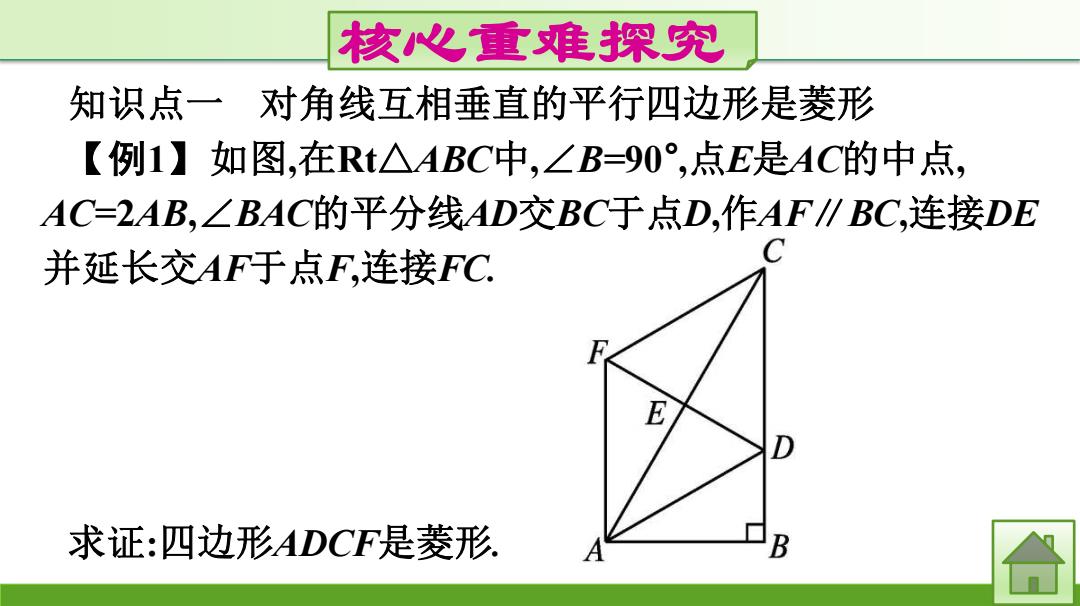
核心重难探究 知识点一 对角线互相垂直的平行四边形是菱形 【例1】如图,在Rt△ABC中,∠B=90° ,点E是AC的中点, AC=2AB,∠BAC的平分线AD交BC于点D,作AF∥BC,连接DE 并延长交AF于点F,连接FC. 求证:四边形ADCF是菱形

思路点拨:(I)△AEF与△CED全等吗?线段AF与CD是否相 等? (2)四边形ADCF是平行四边形吗?为什么? 3)△AED与△ABD全等吗?∠AED等于多少度? 合
思路点拨:(1)△AEF与△CED全等吗?线段AF与CD是否相 等? (2)四边形ADCF是平行四边形吗?为什么? (3)△AED与△ABD全等吗?∠AED等于多少度?

证明:.AF∥CD, '.∠EAF=∠ECD,∠EFA=∠EDC. 又点E是AC的中点,'.AE=CE, .△AEF2△CED,'.AF=CD. 又AF∥CD,'.四边形ADCF是平行四边形. 在△AED和△ABD中,由题意, 知AE=AB,∠EAD=∠BAD,AD=AD,'.△AED≌△ABD, '.∠AED=∠B=90°,即DF⊥AC. ∴.四边形ADCF是菱形
证明:∵AF∥CD, ∴∠EAF =∠ECD,∠EFA=∠EDC. 又点E是AC的中点,∴AE=CE, ∴△AEF≌△CED,∴AF =CD. 又AF∥CD,∴四边形ADCF是平行四边形. 在△AED和△ABD中,由题意, 知AE=AB,∠EAD=∠BAD,AD=AD,∴△AED≌△ABD, ∴∠AED=∠B=90° ,即DF⊥AC. ∴四边形ADCF是菱形

【方法归纳】 在进行菱形的判定与识别时,要注意它是四边形还是平行四 边形,并根据条件选择合适的判定方法.若是平行四边形,则再 需要下面任一条件,即可判定该平行四边形为菱形:(1)邻边相 等;2)对角线互相垂直;3)每条对角线平分一组对角:
【方法归纳】 在进行菱形的判定与识别时,要注意它是四边形还是平行四 边形,并根据条件选择合适的判定方法.若是平行四边形,则再 需要下面任一条件,即可判定该平行四边形为菱形:(1)邻边相 等;(2)对角线互相垂直;(3)每条对角线平分一组对角