
Electrostatic by Using the Scalar Potential of Electrostatic Field) 己知在线性介质中静电场的总能量为 W=1 [E.Ddt (3.14) 2 在静电情形下,能量W可以用电势0和电荷p表示。由 E=-Vo和V.D=p可得 E.D=-Vo.D=-V.(oD)+oV.D (3.15) =-V.(pD)+p0 因此 W=Jaodr-2f-(o0dr (3.16) 即 (3.17) 若我们考虑的势体系的总能量,则上式的体积分是对全空间进行的。 那么上式右边第二项的面积分是对无穷大的闭合曲面进行的。有限的 电荷体系在无穷远处的电势。~,电场~,而面积,故在r∞ 时,面积分项的值等于零,故有 W= (3.18) 讨论:对W=:的使用需要注意以下儿点 a.适用于静电场,线性介质; b.适用于求总能量(如果求某一部分能量时,面积分项,D);
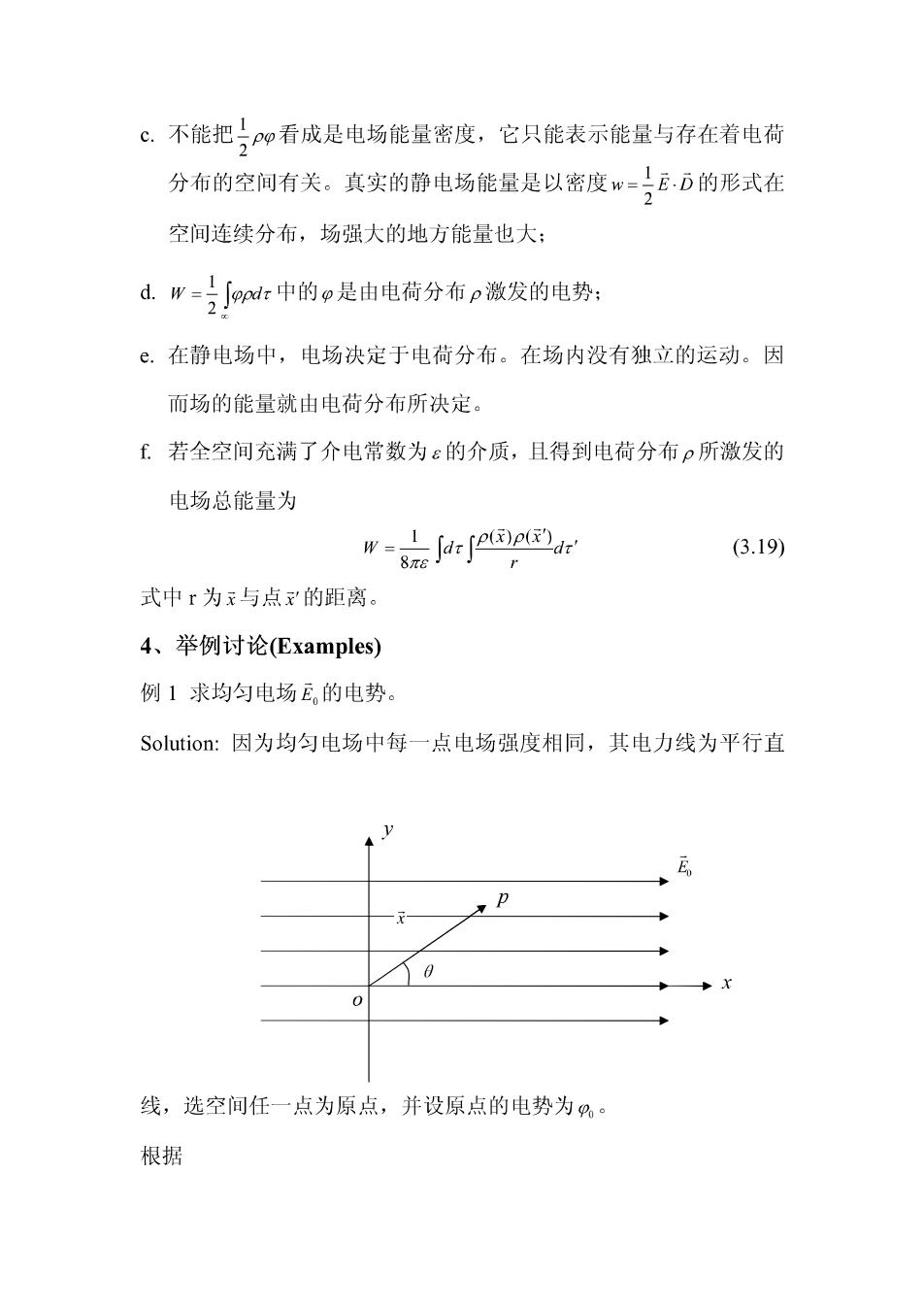
c.不能把,m看成是电场能量密度,它只能表示能量与存在着电荷 分布的空间有关。真实的静电场能量是以密度w=ED的形式在 空间连续分布,场强大的地方能量也大: dW=2小o:中的o是由电荷分布p激发的电势: .在静电场中,电场决定于电荷分布。在场内没有独立的运动。因 而场的能量就由电荷分布所决定。 f.若全空间充满了介电常数为ε的介质,且得到电荷分布ρ所激发的 电场总能量为 (3.19) 式中r为元与点x的距离。 4、举例讨论(Examples) 例1求均匀电场E。的电势。 Solution::因为均匀电场中每一点电场强度相同,其电力线为平行直 线,选空间任一点为原点,并设原点的电势为,。 根据

pp)-op)=-E. (p)-p0)--[E.di 故得到 pp)=。-Edi =9。-E。·元 这里有个参考点选择问题。 例2均匀带电的无限长直导线的电荷密度为元,求空间的电势。 日 电荷源 dq'=Adz 场 R Solution: 选取柱坐标:源点的坐标为(0,z),场点的坐标为R,0),考虑到导线 是无限长,电场强度显然与z无关。 这里先求电场强度,后求电标势。由于 F=(R-0)方+(0-z=R6-z分,电荷元为dg=1d,因此 停— 1 z分 4,(R2+2 令 z'=Rtg0,dz'=Rsec20d0 且

dz' sec2aie (R2+22)p=」 R21+tg20)p sec2θ do R2sec0 1 -do =JRisec R2do= cose 2 而 z'dz Rtg0 (R2+22)0-」 d8= ,Rsim d0=0 R2sec3 2 故 E= 4π60 p 2πER 设po点与导线的垂直距离为Ro,则p点到po点的电势差为 o(R)-p(R.)=-fE.dT =-【3Ri(aR+o+边 dR R = RR=- 2i 2r6R,2n6 R 若选p为参考点(即p(R)=0),则 (R)=-元n R 2π6R

课堂及课后思考: 均匀带电量为O的圆盘,其半径为R,求周围电场及其电标势