《电磁场与电磁波》课程教学资源（文献资料）一些有用的数学结论

附录 1一些有用的数学结论1.失量关系矢量6、、e,、e.为单位失量，其方向分别为x、y、z三个坐标轴的正方向,如图B.1所示。12图B.1单位矢量é、e,、e.在坐标轴上的正方向任何矢量都可用这些单位失量进行表示，例如失量a可以表示为a=ea,+éa,+éa.矢量a的模为a=a+a,+a设失量6为b=eb +e,b,+e,b.则矢量的加减运算规则为a+b=e.(a,+b)+,(a,+b,)+e(a +b.)a-b=e(a,-b)+,(a,-b,)+e(a.-b)矢量的标量积(点乘)为a.b=a,b.+a,b,+a.b.=abcoso式中为矢量a与b之间的夹角矢量的矢量积（又乘）为

附录 1 一些有用的数学结论 1. 矢量关系 矢量 x e  、 y e  、 z e  为单位矢量，其方向分别为 x、y、z 三个坐标轴的正方向,如图 B.1 所 示。 图 B.1 单位矢量 x e  、 y e  、 z e  在坐标轴上的正方向 任何矢量都可用这些单位矢量进行表示，例如矢量 a 可以表示为 x x y y z z a e a e a e a = + + 矢量 a 的模为 2 2 2 a = ax + ay + az 设矢量 b 为 x x y y z z b e b e b e b = + + 则矢量的加减运算规则为 ( ) ( ) ( ) x x x y y y z z z a b e a b e a b e a b + = + + + + + ( ) ( ) ( ) x x x y y y z z z a b e a b e a b e a b − = − + − + − 矢量的标量积(点乘)为 cos x x y y z z a b a b a b a b ab  = + + =  式中  为矢量 a 与 b 之间的夹角。 矢量的矢量积（叉乘）为

eée.axb= a, a-2(ab-a.b)-2,(ab -a.b)+2(a,b,-a,b)-C (假设)bxb,b.矢量积的模为C=ax6|=absino式中为矢量a与之间的夹角。矢量C既垂直于也垂直于b，形同下例ee,eexe,=1 3 0-e010微分算子√（del）在直角坐标系中表示为V=20++2该算子如同上面描述的矢量和一样，也可进行标量乘和矢量乘。假设u为标量，则算子与u的乘积即为u的梯度（grad u）%%+%Fea矢量的散度定义为aoxoyz矢量a的旋度定义为eeeVxa=00axyOzayazax02aaya.算子自身的标量乘为在球形极坐标下，矢量a被表述为a=éa, +égag+é,ag式中é,是指向r增加方向的单位失量，e是指向增加方向的单位矢量，é。是指向の增加

x y z x y z x y z e e e a b a a a b b b  = = ( ) ( ) ( ) x y z z y y x z z x z axby aybx e a b − a b − e a b − a b + e −    =C （假设） 矢量积的模为 C a b ab =  = sin 式中  为矢量 a 与 b 之间的夹角。 矢量 C 既垂直于 a 也垂直于 b ，形同下例 z x y z x y e e e e e e        = = 0 1 0 1 0 0 微分算子  （del）在直角坐标系中表示为 z e y e x ex y z   +   +    =    该算子如同上面描述的矢量 a 和 b 一样，也可进行标量乘和矢量乘。假设 u 为标量，则算子 与 u 的乘积即为 u 的梯度（grad u ） z u e y u e x u u ex y z   +   +    =    矢量 a 的散度定义为 x y z a a a a x y z     = + +    矢量 a 的旋度定义为 x y z x y z e e e a x y z a a a      =    ( ) ( ) ( ) y a x a e z a x a e z a y a e y x z z x y z y x   −   +   −   −   −   =    算子自身的标量乘为 2 2 2 2 2 2 2 =    +   +    = x y z 在球形极坐标下，矢量 a 被表述为 r r a e a e a e a = + +     式中 r e  是指向 r 增加方向的单位矢量，  e  是指向  增加方向的单位矢量，  e  是指向  增加

方向的单位失量，如图B.2所示。图B.2坐标转换的示意在球形极坐标下，标量u的梯度（grad u）被表述为Vu=e,Ou+e,louOu2.10+0sh000Or在球形极坐标下，矢量的散度和旋度被表述为da&cV.a-rarrsinep-sino%(,)+()%Vxa=é,-an标量三重积a-(b ×c):括号表示首先要进行失量积，而后再求a与(b×c)的“点乘"。如果a等于b或，则标量三重积为零，这是因为(6×)所得的结果是一个既垂直于b也垂直于的矢量，如果这个矢量再与6或C求标量积，则由于二者垂直，所以其结果为零。进一步地，对于任意矢量c有V.(Vxc)=0标量三重积中的矢量可以顺序交换位置而结果不变，即a.(bxc)=b.(cxa)=t.(axb)失量三重积ax(6×c):括号表示首先要进行(6×c)的矢量积，而后再求a与(6×c)的“叉乘"。对于任意矢量

方向的单位矢量，如图 B.2 所示。 图 B.2 坐标转换的示意 在球形极坐标下，标量 u 的梯度（grad u ）被表述为        +   +    = u r e u r e r u u er sin   1  1 在球形极坐标下，矢量 a 的散度和旋度被表述为 2 2 1 1 1 ( ) ( sin ) sin sin r a a r a a r r r r            = + +    1 1 1 [ ( sin ) ] [ sin ( )] [ ( ) ] sin sin r r r a a a a e a e ra e ra r r r r r                      = − + − + −       标量三重积 a b c   ( ) : 括号表示首先要进行矢量积，而后再求 a 与 ( ) b c  的“点乘”。如果 a 等于 b 或 c ，则 标量三重积为零，这是因为 ( ) b c  所得的结果是一个既垂直于 b 也垂直于 c 的矢量，如果 这个矢量再与 b 或 c 求标量积，则由于二者垂直，所以其结果为零。进一步地，对于任意矢 量 c 有     = ( ) 0 c 标量三重积中的矢量可以顺序交换位置而结果不变，即 a b c   ( ) = b c a   ( ) = c a b   ( ) 矢量三重积 a b c   ( ) : 括号表示首先要进行 ( ) b c  的矢量积，而后再求 a 与 ( ) b c  的“叉乘”。对于任意矢量

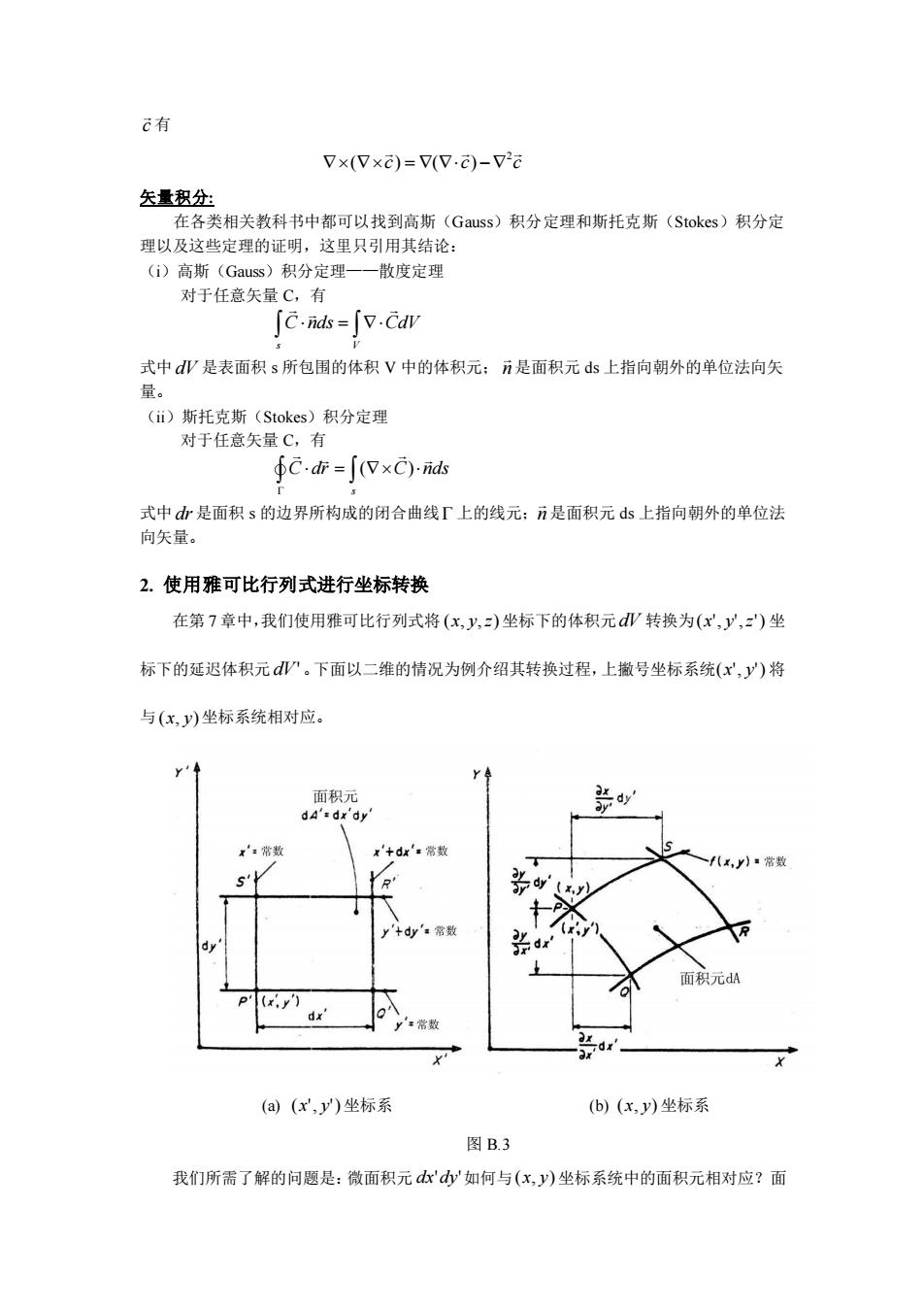
有Vx(Vx)= V(V.)-V2矢量积分：在各类相关教科书中都可以找到高斯（Gauss）积分定理和斯托克斯（Stokes）积分定理以及这些定理的证明，这里只引用其结论：（i）高斯（Gauss）积分定理一散度定理对于任意失量C，有Jc.nds=Jv.Cdv式中dV是表面积s所包围的体积中的体积元；n是面积元ds上指向朝外的单位法向矢量。（i）斯托克斯（Stokes）积分定理对于任意矢量 C，有fc.dr= J(VxC).nds式中dr是面积s的边界所构成的闭合曲线r上的线元；n是面积元ds上指向朝外的单位法向矢量。2.使用雅可比行列式进行坐标转换在第7章中，我们使用雅可比行列式将(x,y,=)坐标下的体积元dV转换为(x,y,2)坐标下的延迟体积元dV。下面以二维的情况为例介绍其转换过程，上撒号坐标系统(x,J")将与(x,J)坐标系统相对应。dyYR(x.y)(a)(x,y")坐标系(b) (x,J)坐标系图B.3我们所需了解的问题是：微面积元dxdy如何与(x,y)坐标系统中的面积元相对应？面

c 有 2   =   − ( ) ( ) c c c 矢量积分: 在各类相关教科书中都可以找到高斯（Gauss）积分定理和斯托克斯（Stokes）积分定 理以及这些定理的证明，这里只引用其结论： （i）高斯（Gauss）积分定理——散度定理 对于任意矢量 C，有 s V C nds CdV  =    式中 dV 是表面积 s 所包围的体积 V 中的体积元； n 是面积元 ds 上指向朝外的单位法向矢 量。 （ii）斯托克斯（Stokes）积分定理 对于任意矢量 C，有 ( ) s C dr C nds   =     式中 dr 是面积 s 的边界所构成的闭合曲线  上的线元； n 是面积元 ds 上指向朝外的单位法 向矢量。 2. 使用雅可比行列式进行坐标转换 在第 7 章中，我们使用雅可比行列式将 (x, y,z) 坐标下的体积元 dV 转换为 (x' , y' ,z') 坐 标下的延迟体积元 dV' 。下面以二维的情况为例介绍其转换过程，上撇号坐标系统 (x' , y') 将 与 (x, y) 坐标系统相对应。 (a) (x' , y') 坐标系 (b) (x, y) 坐标系 图 B.3 我们所需了解的问题是：微面积元 dx'dy' 如何与 (x, y) 坐标系统中的面积元相对应？面

积元dxdy中的直线对应于x-y平面上的曲线，例如x=常数（在x-y平面）对应于f(,J)=常数（在x-j平面)P点的坐标是(x,J),该点对应于(x,)坐标中的p点。假设当从p点移动到Q点时，dx仅仅在方向发生变化，这时有Q点的×坐标=x+dr仅仅在x方向发生变化时×的变化量=x+odrCrQ点的y坐标-y+dx仅仅在x方向发生变化时y的变化量=y+od类似地，可以写出点s的(x,)坐标为aay,ytyay)(x+x+ayay三角形的面积可以根据其坐标用行列式进行表示，如三角形PSQ的面积为1++）Ox(x+0ya用第二行减去第一行，并用第三行减去第一行，则行列式的值应保持不变。这时，三角形的面积为一1[ax +山o[ay ay]0而矩形dA的面积则为三角形面积的两倍，即e

积元 dx'dy' 中的直线对应于 x-y 平面上的曲线，例如 x' =常数（在x'−y'平面） 对应于 f (x, y) =常数（在x − y平面） p' 点的坐标是 (x' , y') ，该点对应于 (x, y) 坐标中的 p 点。假设当从 p' 点移动到 Q' 点时, dx' 仅仅在 x' 方向发生变化，这时有 Q 点的 x 坐标=x+ dx' 仅仅在 x' 方向发生变化时 x 的变化量 = ' ' dx x x x   + Q 点的 y 坐标=y+ dx' 仅仅在 x' 方向发生变化时 y 的变化量 = ' ' dx x y y   + 类似地，可以写出点 s 的 (x, y) 坐标为 （ ' ' dy y x x   + ， ' ' dy y y y   + ） 三角形的面积可以根据其坐标用行列式进行表示，如三角形 PSQ 的面积为                   +   +   +   + ') 1 ' ') ( ' ( ') 1 ' ') ( ' ( 1 2 1 dy y y dy y y x x dx x y dx y x x x x y 用第二行减去第一行，并用第三行减去第一行，则行列式的值应保持不变。这时，三角形的 面积为 ' ' ' ' ' ' 2 1 ' 0 ' ' ' ' 0 ' ' ' 1 2 1 y y y x x y x x dx dy dy y y dy y x dx x y dx x x x y         =                         而矩形 dA 的面积则为三角形面积的两倍，即 ' ' ' ' ' ' y y y x x y x x dA dx dy         =