四、随机变量的分类 通常分为两类: 离散型随机变量 所有取值可以逐个 列举 随机变量 如“取到次品的个数 收到的呼叫数”等. 全部可能取值不仅 无穷多,而且还不能 连续型随机变量 列举,而是充满 一个区间. 例如,“电视机的寿命”,实 际中常遇到的“测量误差”等
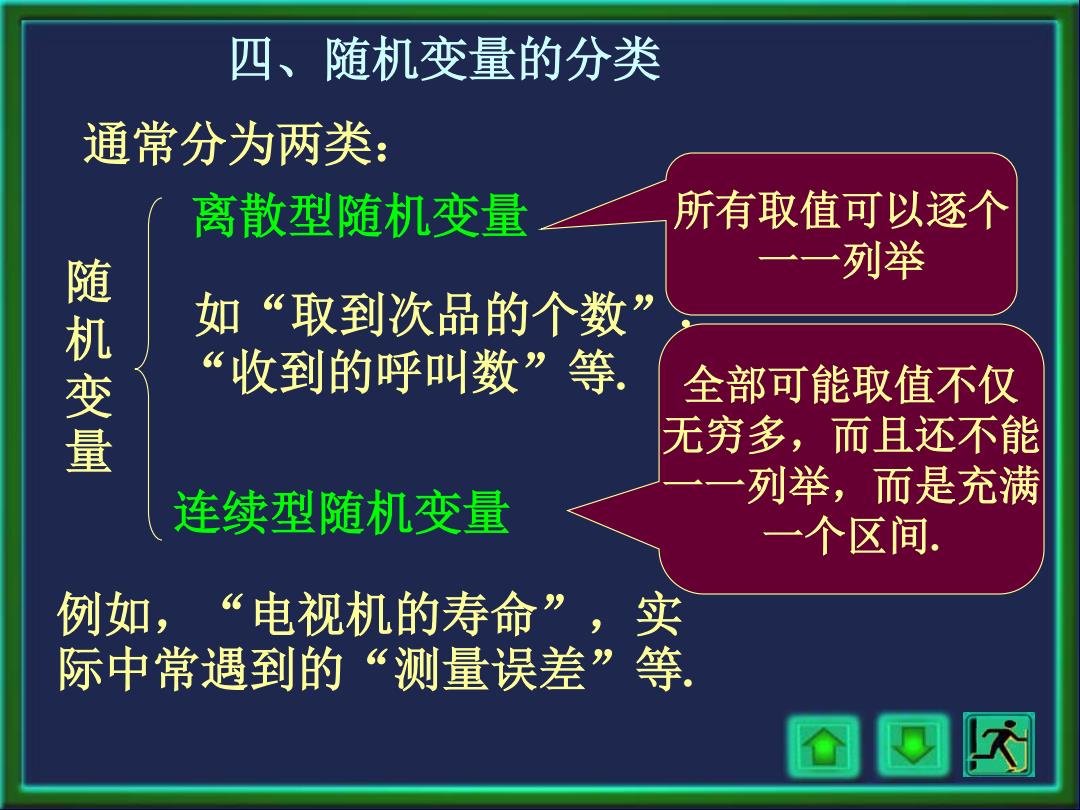
四、随机变量的分类 通常分为两类: 如“取到次品的个数”, “收到的呼叫数”等. 随 机 变 量 离散型随机变量 连续型随机变量 所有取值可以逐个 一一列举 例如,“电视机的寿命”,实 际中常遇到的“测量误差”等. 全部可能取值不仅 无穷多,而且还不能 一一列举,而是充满 一个区间

随机变量 离散型随机变量 连续型随机变量 这两种类型的随机变量因为都是随机变 量,自然有很多相同或相似之处;但因其取 值方式不同,又有其各自的特点。 学习时请注意它们各自的特点和描述方法
这两种类型的随机变量因为都是随机变 量,自然有很多相同或相似之处;但因其取 值方式不同,又有其各自的特点. 随 机 变 量 连续型随机变量 离散型随机变量 学习时请注意它们各自的特点和描述方法

第二章第二节 离散型随机变量 设X是一个离散型随机变量,它可能 取的值是x1,X2, 为了描述随机变量X,我们不仅需 要知道随机变量X的取值,而且还应知道 取每个值的概率
设X是一个离散型随机变量,它可能 取的值是 x1, x2 , … . 为了描述随机变量 X ,我们不仅需 要知道随机变量X的取值,而且还应知道 X取每个值的概率. 第二章 第二节 离散型随机变量
例1 从中任取3个球 取到的白球数X是一个随机变量 X可能取的值是0,1,2 取每个值的概率为 PX-0- C3 C 10 且 产Ax=l PX-I)-CC 6 10 这样,我们就掌握了这个 随机变量取值的概率规律. P(X=2)= 3 c 10
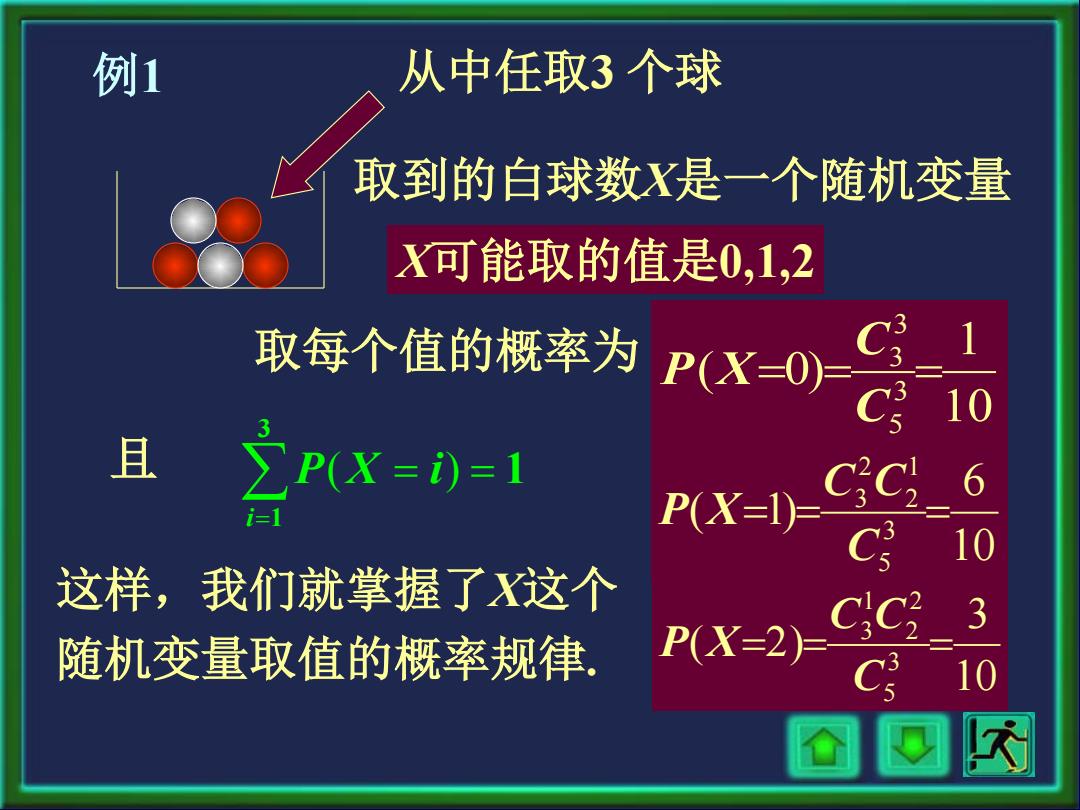
这样,我们就掌握了X这个 随机变量取值的概率规律. 从中任取3 个球 取到的白球数X是一个随机变量 X可能取的值是0,1,2 取每个值的概率为 10 1 ( 0) 3 5 3 3 = = = C C P X 10 6 ( 1) 3 5 1 2 2 3 = = = C C C P X 10 3 ( 2) 3 5 2 2 1 3 = = = C C C P X 例1 且 ∑= = = 3 1 1 i P(X i)

离散型随机变量概率分布的定义 定义1:设x(k=1,2,…)是离散型随机变 量X所取的一切可能值,称 PCX=x)=Pk2=1,2,. 为离散型随机变量X的概率分布或分布 律,有的书上也称概率函数 其中Pk(k=1,2,.)满足: 用这两条性质判断 (1)P≥0, k=1,2,… 一个函数是否是 (2)∑P=l 概率分布
其中 pk (k=1,2, …) 满足: ≥ 0, (1)pk k=1,2, … ∑ = k ( pk 1 2) 定义1:设xk(k=1,2, …)是离散型随机变 量X所取的一切可能值,称 P(X=xk )=pk, k=1,2,… 为离散型随机变量X的概率分布或分布 律,有的书上也称概率函数. 用这两条性质判断 一个函数是否是 概率分布 一、离散型随机变量概率分布的定义