
二元函数的图象: 二元函数z=f(x,y)能够用三维空间R的 几何图象表示.称R中点集 (x.y.f(x.y))(x.y)eD 为函数z=f(x,y),(x,y)∈D的图象 二元函数f的图象 =f(x,y) 通常是一张曲面. 的定义域D便是这 张曲面在xoy平面 上的投影 上页 返回
二元函数的图象: 3 二元函数z f xy = (, )能够用三维空间R 的 3 几何图象表示.称R 中点集: {( xyf xy xy D , , (, )(, ) ) ∈ } 为函数z f xy xy D = ( , ), ( , ) . ∈ 的图象 二元函数 f 的图象 通常是一张曲面. f 的定义域D便是这 张曲面在xoy平面 上的投影

例如,z=siny 图形如右图 例如,x2+y2+z2=a2 如左图球面 D={x,y)x2+y2≤a2. 单值分支:z=√02-x2-y2 z=-Va2-x2-y2, 上页 返回
x y z o z = sin xy 例如, 图形如右图. 2 2 2 2 x + y + z = a 例如, 如左图球面. {( , ) }. 2 2 2 D = x y x + y ≤ a 2 2 2 z = a − x − y . 2 2 2 z = − a − x − y 单值分支:

2.定义域: 例5.求定义域: ny国= Iny V2+y2-1 y) 上页 下页 返回
2. 定义域: 例5.求定义域: 2 2 2 2 9 ( ). ( , ) ; 1 x y i f xy x y − − = + − 2 ln () (, ) . ln( 1) y ii f x y y x = − +
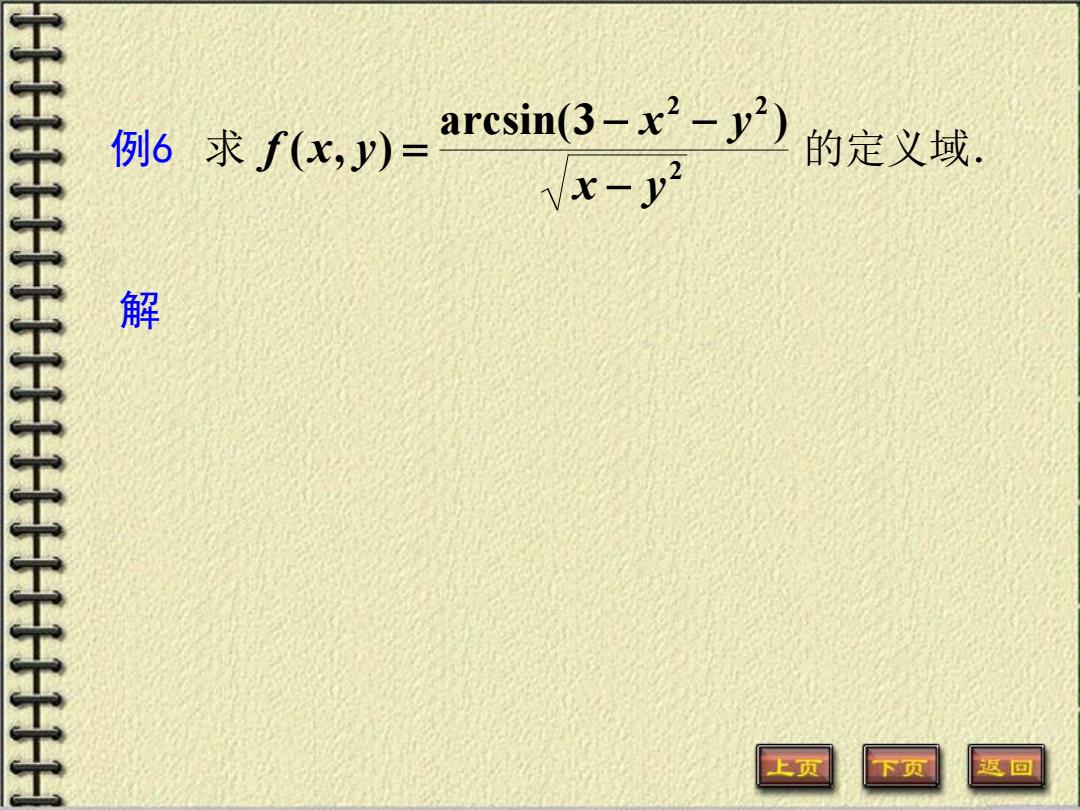
例6求fx,y)= arcsin(3-x2-y2) 的定义域 /x-y2 解 上页 下页 返回
例6 求 2 的定义域. 2 2 arcsin(3 ) ( , ) x y x y f x y − − − = 解

3.二元函数求值 70=2x-求).小) 例8.f(x,y)=ln1+x2+y2),求f(pcos0,psin0) 上页 下页 返回
3. 二元函数求值 2 7. ( , ) 2 3 , (1, 1) , 1 , . y f xy x y f f x =− − 例 求 2 2 例8. ( , ) ln(1 ), ( cos , sin ) f xy x y f = ++ 求 ρ θρ θ