
第二章矩阵 ◆矩阵的运算 ◆几种特殊矩阵 ◆分块矩阵 ◆逆矩阵 ◆初等矩阵
第二章 矩 阵 矩阵的运算 几种特殊矩阵 分块矩阵 逆矩阵 初等矩阵

§2.1 矩阵的运算 一、矩阵的概念 术语:矩阵(数域F上的矩阵),记作A,Amxn,(a)mxm 几种特殊矩阵 ()行数与列数都等于n的矩阵A,称为n阶 方阵.也可记作An (2)向量是特殊的矩阵,例如a=(a1,42,…,4n), 为1Xn矩阵. b2 B= 为n×l矩阵
几种特殊矩阵 (1)行数与列数都等于n 的矩阵 A,称为 n 阶 . 方阵.也可记作 An (2)向量是特殊的矩阵, 例如α = (aa a 1 2 ,,, , n ) 为1×n矩阵. 1 2 n b b b β = 为n×1矩阵 §2.1 矩阵的运算 一、矩阵的概念 术语:矩阵(数域F上的矩阵),记作 , ,( ) AA a m n ij m n × ×
(3)元素全为零的矩阵称为零矩阵,m×n零矩阵, 记作0xm或O 【注】不同阶数的零矩阵是不相等的. 例如 0 ≠(0000 (4)形如 的方阵称为对角阵 不全为0 记作 A=diag(21,元2,…,元n)
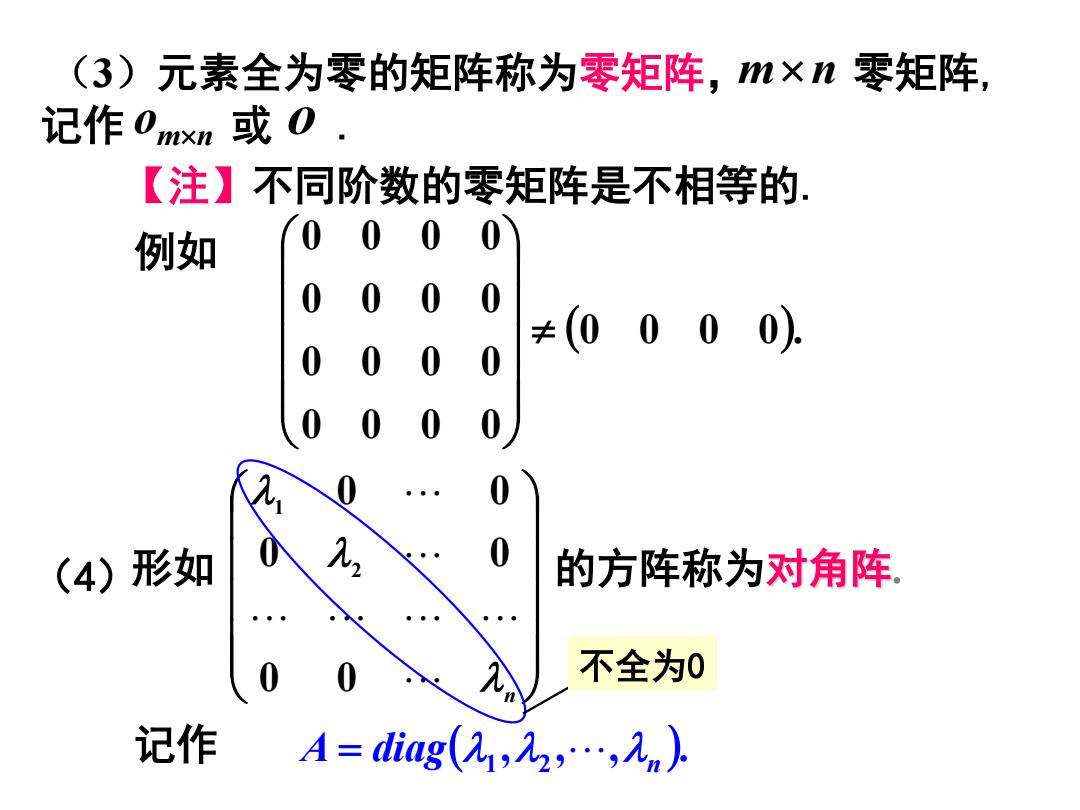
(3)元素全为零的矩阵称为零矩阵,m × n 零矩阵, 记作 om×n 或 o . 【注】不同阶数的零矩阵是不相等的. (0 0 0 0). 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 ≠ 例如 λ n λ λ 0 0 0 0 0 0 2 1 (4)形如 的方阵称为对角阵. 不全为0 记作 ( , , , ). 1 2 n A = diag λ λ λ

(5)方阵 称为单位矩阵(或单位阵) E=E= 全为1 一1 12 (6)-A= -L21 一L22 称为A的负矩阵 一lmn 术语两个矩阵的行数相等,列数相等时,称为同型矩阵
(5)方阵 = = 0 0 1 0 1 0 1 0 0 E E n 称为单位矩阵(或单位阵) 全为1 术语 两个矩阵的行数相等,列数相等时,称为同型矩阵. ( ) 11 12 1 21 22 2 1 1 6 n n m m mn aa a aa a A aa a −− − −− − − = −− − 称为A的负矩阵

矩阵相等的定义 两个矩阵A=(4,)与B=(b,)为同型矩阵,并且对应 元素相等,即a,=b,(i=1,2,…,mj=1,2,…,n) 则称矩阵A与B相等,记作A=B. 1.矩阵的加法 定义设有两个m×n矩阵A=(a人B=(b,)那么矩阵 A与B的和记作A+B,规定为 a11+b1 a2+b2 …L1n+bm a21+b21a2z+b2 A+B= …a2n+b2m +b 说明只有同型矩阵才能进行加法运算
1.矩阵的加法 说明 只有同型矩阵才能进行加法运算. + + + + + + + + + + = m m m m mn mn n n n n a b a b a b a b a b a b a b a b a b A B 1 1 2 2 21 21 22 22 2 2 11 11 12 12 1 1 设有两个 矩阵 那么矩阵 与 的和记作 ,规定为 m × n A (a ), B (b ), = ij = ij A B A+ B 定义 两个矩阵 为同型矩阵,并且对应 元素相等,即 Aa Bb = = ( ij)与 ( ij) a b (i 1,2, ,m; j 1,2, ,n), ij = ij = = 则称矩阵A与B相等,记作A = B. 矩阵相等的定义