核心重难探究 解:如图所示,连接OC,OB⊥CD,O为圆心, ∴.CE-CD=3. A 2 设OC=OB=r,则OE=r-2. 在Rt△OCE中,由勾股定理, 得2+32=,解得是 D E “⊙0的半径为是 B cm. 导航页
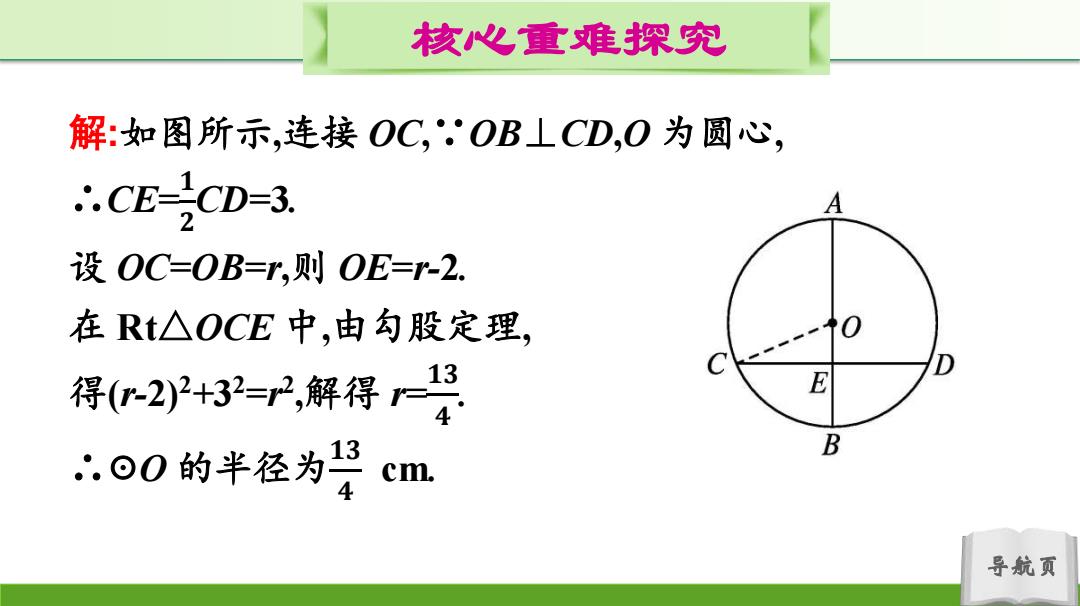
导航页 核心重难探究 解:如图所示,连接 OC,∵OB⊥CD,O 为圆心, ∴CE=𝟏 𝟐 CD=3. 设 OC=OB=r,则 OE=r-2. 在 Rt△OCE 中,由勾股定理, 得(r-2)2 +3 2 =r2 ,解得 r= 𝟏𝟑 𝟒 . ∴☉O 的半径为𝟏𝟑 𝟒 cm

核心重难探究 【方法归纳】 解决与弦有关的问题时,往往需构造以半径、弦心距和弦长 的一半为三边的直角三角形,利用垂径定理和勾股定理求解 即可. 导航页
导航页 核心重难探究 【方法归纳】 解决与弦有关的问题时,往往需构造以半径、弦心距和弦长 的一半为三边的直角三角形,利用垂径定理和勾股定理求解 即可

核心重难探究 知识点二:垂径定理及其推论的应用 免疫区 【例2】为防止禽流感蔓延,某地规定: 捕杀区 0。 离疫点3千米范围内为捕杀区,所有禽类 B 全部捕杀;离疫点3至5千米范围内为免 疫区,所有禽类强制免疫;同时,对捕杀区和免疫区内的村庄、 道路实行全封闭管理现有一条笔直的公路AB通过禽流感病 区,如图,O为疫点,在捕杀区内的公路CD长为4千米,问这条公 路在该免疫区内有多少千米? 导航页
导航页 核心重难探究 知识点二:垂径定理及其推论的应用 【例2】为防止禽流感蔓延,某地规定: 离疫点3千米范围内为捕杀区,所有禽类 全部捕杀;离疫点3至5千米范围内为免 疫区,所有禽类强制免疫;同时,对捕杀区和免疫区内的村庄、 道路实行全封闭管理.现有一条笔直的公路AB通过禽流感病 区,如图,O为疫点,在捕杀区内的公路CD长为4千米,问这条公 路在该免疫区内有多少千米?

核心重难探究 思路点拨:过点O作OE⊥CD交CD于点E,连接OC,OA,在 Rt△OCE中求出 ,在Rt△OAE中求出 进而求出AC,求出答案 导航页
导航页 核心重难探究 思路点拨:过点O作OE⊥CD交CD于点E,连接OC,OA,在 Rt△OCE中求出 ,在Rt△OAE中求出 , 进而求出AC,求出答案