
概率伦与散理统针」 第三章 多维随机变量及其分布 习题课 一、重点与难点 二、主要内容 三、典型例题
一、重点与难点 二、主要内容 三、典型例题 第三章 多维随机变量及其分布 习 题 课

概率伦与款程统外 一、重点与难点 1.重点 二维随机变量的分布 有关概率的计算和随机变量的独立性 2.难点 条件概率分布 随机变量函数的分布
一、重点与难点 1.重点 二维随机变量的分布 有关概率的计算和随机变量的独立性 2.难点 条件概率分布 随机变量函数的分布
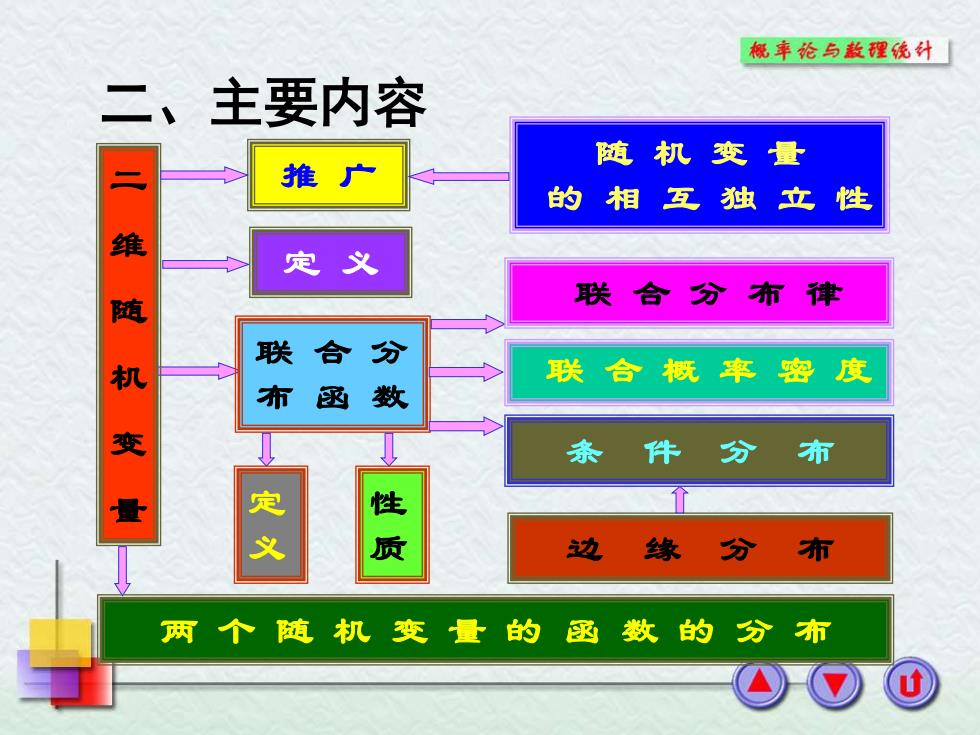
概车纶与款理统外 二、主要内容 随机变量 二 推 的相互独立性 维 定义 随 联合分布律 联 合 分 机 联合概率密度 布函 数 变 条件 分布 定 性 义 质 边 缘分布 两个随机变量的函数的分布
定 义 联 合 分 布 函 数 联 合 分 布 律 联 合 概 率 密 度 边 缘 分 布 条 件 分 布 两 个 随 机 变 量 的 函 数 的 分 布 随 机 变 量 的 相 互 独 立 性 定 义 性 质 二 维 随 机 变 量 推 广 二、主要内容
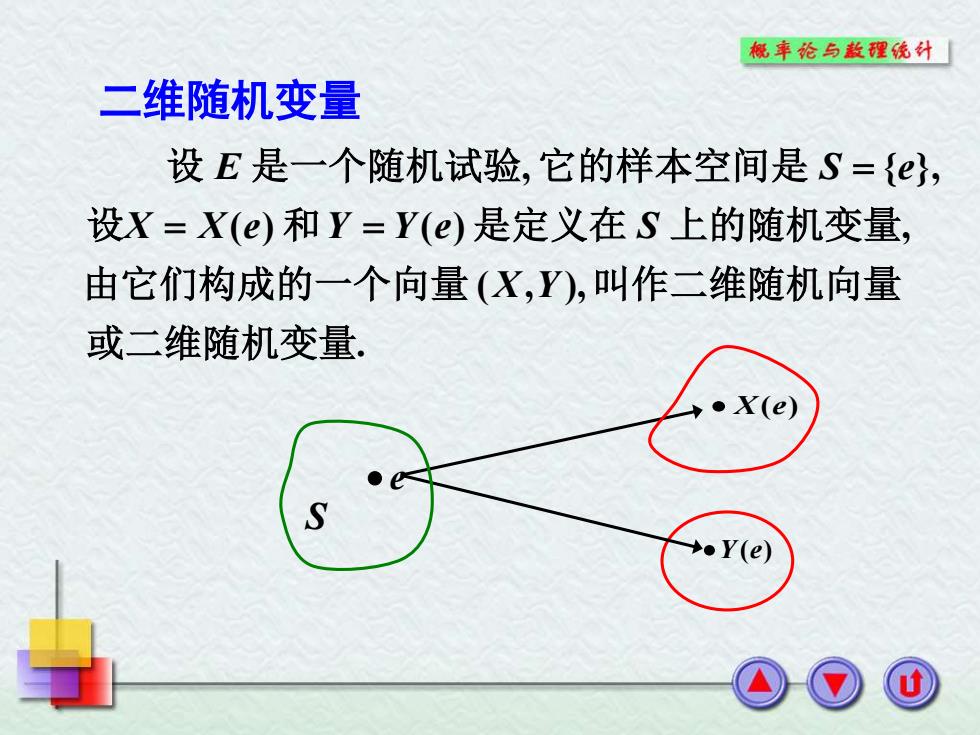
概華论与款醒硫外「 二维随机变量 设E是一个随机试验,它的样本空间是S={, 设X=X(e)和Y=Y(e)是定义在S上的随机变量, 由它们构成的一个向量(X,),叫作二维随机向量 或二维随机变量. ●X(e) →eY(e)
. ( , ), ( ) ( ) , , { }, 或二维随机变量 由它们构成的一个向量 叫作二维随机向量 设 和 是定义在 上的随机变量 设 是一个随机试验 它的样本空间是 X Y X X e Y Y e S E S e = = = 二维随机变量 • e •Y(e) S • X(e)

概车纶与款理统外 二维随机变量的分布函数 ()定义 设(X,Y)是二维随机变量,对于任意实数x, y,二元函数: F(x,y)=P{(X≤x)∩(Y≤y)}=P{X≤x,Y≤y} 称为二维随机变量(X,Y)的分布函数,或称为随 机变量X和Y的联合分布函数
(1) 定义 . ( , ) , ( , ) {( ) ( )} { , } , : ( , ) , , 机变量 和 的联合分布函数 称为二维随机变量 的分布函数 或称为随 二元函数 设 是二维随机变量 对于任意实数 X Y X Y F x y P X x Y y P X x Y y y X Y x = = 二维随机变量的分布函数