
概车纶与款理统外 第一节 大数定律 一、问题的引入 二、基本定理 三、典型例题 四、小结
第一节 大数定律 一、问题的引入 二、基本定理 三、典型例题 四、小结
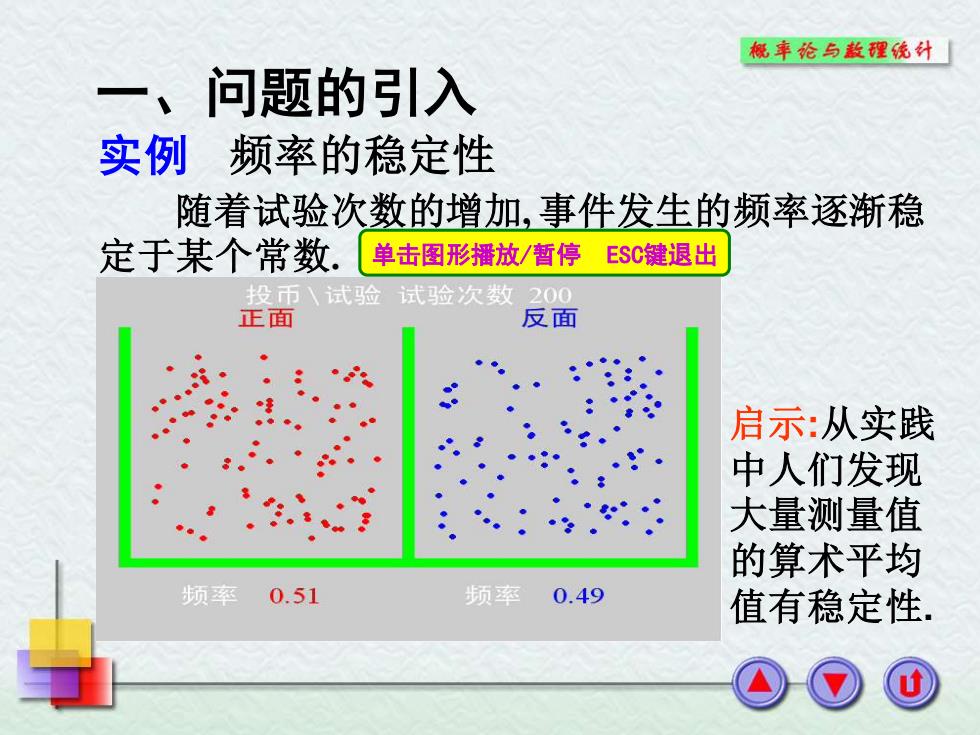
概華论与款程统外 一、问题的引入 实例频率的稳定性 随着试验次数的增加,事件发生的频率逐渐稳 定于某个常数 ,单击图形播放/暂停ESC键退出 投币试验试验次数 200 正面 反面 启示:从实践 中人们发现 大量测量值 的算术平均 频率 0.51 频率 0.49 值有稳定性
一、问题的引入 实例 频率的稳定性 随着试验次数的增加, 事件发生的频率逐渐稳 定于某个常数. 启示:从实践 中人们发现 大量测量值 的算术平均 值有稳定性. 单击图形播放/暂停 ESC键退出

概车纶与款理统外 二、基本定理 定理一(契比雪夫定理的特殊情况) 契比雪夫 设随机变量X1,X2,.,X,.相互独立 且具有相同的数学期和方差:E(Xk)=4, D(Xk)=o2(k=1,2,),作前n个随机变量 的算术平均X=之X,则对于任意正 n k= 数ε有 lim P(X-uK&)=lim 10o -→0 空-水-
二、基本定理 定理一(契比雪夫定理的特殊情况) 数 有 的算术平均 则对于任意正 作 前 个随机变量 且具有相同的数学期望和方差: 设随机变量 相互独立 , 1 ( ) ( 1, 2, ), ( ) , , , , , , 1 2 1 2 = = = = = n k k k k n X n X D X k n E X X X X 契比雪夫 1. 1 lim {| | } lim 1 = − = − = → → n k k n n X n P X P

概率伦与款理统外 二、基本定理 定到 表达式的意义 X-4K是一个随机事件等式表 且 明,当n→oo时这个事件的概率趋于, D( 即对于任意正数&,当n充分大时,不 的身 等式|X-4Ke成立的概率很大 数ε有
定理一(契比雪夫定理的特殊情况) 数 有 的算术平均 则对于任意正 作 前 个随机变量 且具有相同的数学期望和方差: 设随机变量 相互独立 , 1 ( ) ( 1, 2, ), ( ) , , , , , , 1 2 1 2 = = = = = n k k k k n X n X D X k n E X X X X 1. 1 lim {| | } lim 1 = − = − = → → n k k n n X n P X P 表达式的意义 | | . , , , 1, {| | } , 等 式 成立的概率很大 即对于任意正数 当 充分大时 不 明 当 时这个事件的概率趋于 是一个随机事件 等式表 − → − X n n X 二、基本定理

概车纶与款理统外 证明1 2x]-2Aw=4 客]-2w- 由契比雪夫不等式可得 a-a小1- 在上式中令n→oo,并注意到概率不能大于1,则 PtnEx.-n<ej-1
证明 ( ) 1 1 1 1 = = = n k k n k k E X n X n E , 1 = n = n ( ) 1 1 1 2 1 = = = n k k n k k D X n X n D , 1 2 2 2 n n n = = 由契比雪夫不等式可得 1 , 1 2 2 1 n X n P n k k − − = 在上式中令n → , 并注意到概率不能大于1, 则 1. 1 1 = − = n k Xk n P