
概華论与款醒硫外 第四章 随机变量的数字特征 习题课 一、重点与难点 二、主要内容 三、典型例题
一、重点与难点 二、主要内容 三、典型例题 第四章 随机变量的数字特征 习 题 课

概车纶与款理统外 一、重点与难点 1.重点 数学期望的性质和计算 方差的性质和计算 相关系数的性质和计算 2.难点 数字特征的计算
一、重点与难点 1.重点 数学期望的性质和计算 2.难点 数字特征的计算 方差的性质和计算 相关系数的性质和计算
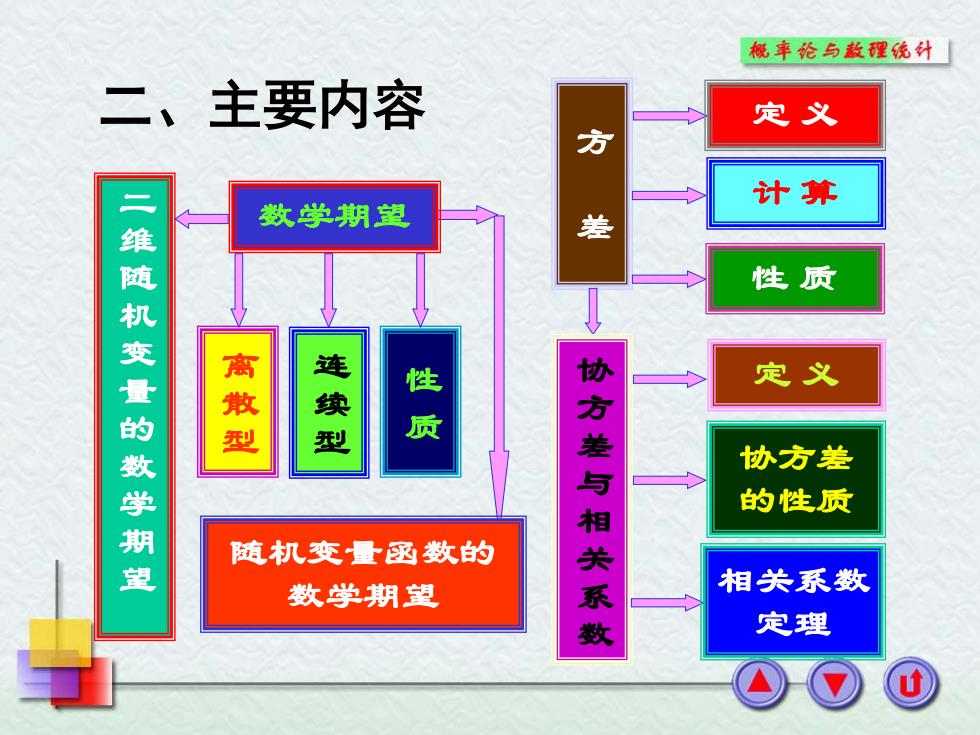
概率伦与款理统外 二、主要内容 定义 方 计算 数学期望 差 性质 维随机变量的数学期望 离 定义 型 连续型 协方差与相关系教 协方差 的性质 随机变量函数的 数学期望 相关系数 定理
二、主要内容 数学期望 方差 离散型 连续型 性质 协方差与相关系数 二维随机变量的数学期望 定 义 计 算 性 质 随机变量函数的 数学期望 定 义 协方差 的性质 相关系数 定理

概车纶与款理统外 离散型随机变量的数学期望 设离散型随机变量X的分布律为 P{X=Xx}=Pk,k=1,2,. 若级数∑xP:绝对收敛, k=1 则称级数∑P为随机变量X的数学期望, k=1 记为E(X),即E(X)=2xPs k
离散型随机变量的数学期望 设离散型随机变量X的分布律为 P{X = x } = p , k = 1,2, . k k , 1 若级数 绝对收敛 k= xk pk , 1 则称级数 x p 为随机变量 X的数学期望 k k k = 记为 E(X), ( ) . 1 = = k 即 E X xk pk

概華论与款醒硫外 连续型随机变量的数学期望 X是连续型随机变量它的概率密度为f(x), 若积分∫f(x)dr绝对收敛, 则称此积分值为连续型随机变量X的数学期望, 记为E(X), 即E(X)=∫rf(xl
连续型随机变量的数学期望 ( ), , ( ) d , E X X xf x x 记为 则称此积分值为连续型随机变量 的数学期望 若积分 绝对收敛 + − E(X) xf (x)dx. + − 即 = X 是连续型随机变量,它的概率密度为f (x)