
电磁学中曾给出按Drude自由电子模型导出了电导率表达 式,解释了欧姆定律: 这里,1是平均自由程,即两次碰撞之间的平均行程, 2mv V是平均热运动速度。 按照气体分子运动论,电子对热导率的贡献应为: 1-2 3 根据经典理论,有: E=2mw=2k,7 2 OE 3 Cy= nkB = -2 3kgT 代入下式 0T2 m 1 于是: = K 2 =3 0 ne'1 2mv L=2.23×10-8Watt-ohm.K2≈实验值 (volt/kelvin)2
电磁学中曾给出按Drude自由电子模型导出了电导率表达 式,解释了欧姆定律: 2 2 ne l mv σ = 这里, 是平均自由程,即两次碰撞之间的平均行程, 是平均热运动速度。 l v 按照气体分子运动论,电子对热导率的贡献应为: 1 3 κ = C vl V 1 3 2 2 2 根据经典理论,有: E = = mv k TB 2 2 2 2 1 3 3 2 3 3 2 B B B nk vl k k T LT T ne l e e mv κ π σ ⎛⎞ ⎛⎞ = = =≈ ⎜⎟ ⎜⎟ ⎝⎠ ⎝⎠ 于是: 8 2 L 2.23 10 Watt-ohm K − − = × ⋅≈ 3 2 V B E C nk T ∂ = = ∂ 2 3 B k T v m = 代入下式 实验值 (volt/kelvin)2

附录:经典电子论对欧姆定律的解释: 无外场时,电子做无规运动,无定向运动,电流=0。 有外电场时,电子虽获得定向加速度,a=-eE m 但因为不断和离子发生碰撞而不会无限制地加速,其定向平均漂移 速度为: -1-1 u=24=2ar=- 假定: y>>1 2 2 mv 所以:j=-neu= 2m y 2mv 平均自由程7与温度无关,而公式中的热运动速度, vc√T 所以也可以定性说明金属电导率和温度关系。 经典观点:以热运动速度运动的全部自由电子都参与了导电。 以后将会看到上述推导和这种观点都不是恰当的。 见胡有秋:电磁学p167;张玉民:电磁学p173
附录:经典电子论对欧姆定律的解释: 无外场时,电子做无规运动,无定向运动,电流 j=0。 有外电场时,电子虽获得定向加速度, 但因为不断和离子发生碰撞而不会无限制地加速,其定向平均漂移 速度为: e a E m = − G JG 1 11 1 22 2 el uu a E mv = = =− τ G G JG 2 2 ne l j neu E m v =− = G G JG 2 2 ne l mv 所以: σ = 平均自由程 与温度无关,而公式中的热运动速度, 所以也可以定性说明金属电导率和温度关系。 经典观点:以热运动速度运动的全部自由电子都参与了导电。 以后将会看到上述推导和这种观点都不是恰当的。 l v T ∝ 见胡有秋:电磁学p167;张玉民:电磁学p173 假定: 1 v u >>

虽然按照经典统计,近似给出了Lorentz常数数值,但其中 给出的电子热容数值在实验中却观察不到,高温下金属的热容数 值只相当于Dulong-Petit数值(Cr=3Wkg),即只看到晶格对热 容的贡献,却看不到电子应有的贡献,C.=3k。-C, 这个矛盾突出暴露了经典理论的不足。即:自由电子对电导贡献 是明显的,但却看不到它对热容和磁化率应有的贡献。 但是实验上完全证实了金属中自由电子的存在,Tolman使 块金属快速的往复运动,可以测到交变电流的产生,这显然 是因为运动中电子具有惯性造成的,用这个实验测出的荷质比 与阴极射线测出的电子荷质比相当,从而证实了金属中的载流 子就是自由移动的电子。 这个无法调和的矛盾在量子力学诞生后才得以正确解决。服 从量子规律的自由电子即可以同时和谐的解释上述性质
虽然按照经典统计,近似给出了 Lorentz 常数数值,但其中 给出的电子热容数值在实验中却观察不到,高温下金属的热容数 值只相当于Dulong-Petit数值 ,即只看到晶格对热 容的贡献,却看不到电子应有的贡献, 这个矛盾突出暴露了经典理论的不足。即:自由电子对电导贡献 是明显的,但却看不到它对热容和磁化率应有的贡献。 ( 3) C Nk V B = 但是实验上完全证实了金属中自由电子的存在,Tolman 使 一块金属快速的往复运动,可以测到交变电流的产生,这显然 是因为运动中电子具有惯性造成的,用这个实验测出的荷质比 与阴极射线测出的电子荷质比相当,从而证实了金属中的载流 子就是自由移动的电子。 这个无法调和的矛盾在量子力学诞生后才得以正确解决。服 从量子规律的自由电子即可以同时和谐的解释上述性质。 3 2 C nk C e BV = ∼

经典理论的另一个困难是不能解释平均自由程。按照经典 理论分析,电子自由程可以达数百个原子间距,而不同类型 的实验结果都表明低温下金属电子的平均自由程可达108个原 子间距,电子沿直线传播可以自由地越过离子实和其他电子而 不受碰撞是经典观念难以理解的,只有在量子力学中才可以得 到解释:)一个传导电子仅受到其它传导电子不频繁的散射是 泡利不相容原理的结果。b)而电子在晶体周期势场中运动的研 究产生了能带论,按照能带论,在严格周期势场中的电子具有 无限的自由程。实际自由程之所以有限是原子振动或其它原因 导致晶体势场偏离周期场的结果。因此可以说是自由电子论促 成了能带论的发展,而能带论则解决了经典理论的全部矛盾
经典理论的另一个困难是不能解释平均自由程。按照经典 理论分析,电子自由程可以达数百个原子间距,而不同类型 的实验结果都表明低温下金属电子的平均自由程可达 108 个原 子间距,电子沿直线传播可以自由地越过离子实和其他电子而 不受碰撞是经典观念难以理解的,只有在量子力学中才可以得 到解释:a) 一个传导电子仅受到其它传导电子不频繁的散射是 泡利不相容原理的结果。b) 而电子在晶体周期势场中运动的研 究产生了能带论,按照能带论,在严格周期势场中的电子具有 无限的自由程。实际自由程之所以有限是原子振动或其它原因 导致晶体势场偏离周期场的结果。因此可以说是自由电子论促 成了能带论的发展,而能带论则解决了经典理论的全部矛盾
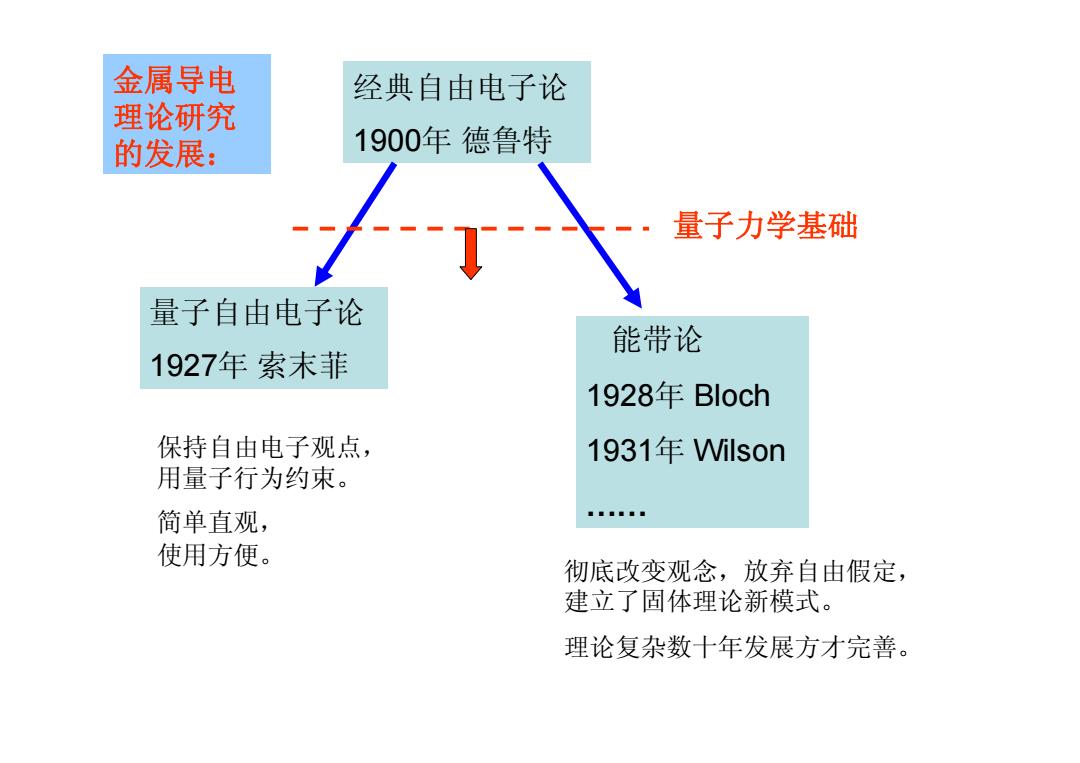
金属导电 经典自由电子论 理论研究 的发展: 1900年德鲁特 量子力学基础 量子自由电子论 能带论 1927年索末菲 1928年Bloch 保持自由电子观点, 1931年Vilson 用量子行为约束。 简单直观, 使用方便。 彻底改变观念,放弃自由假定, 建立了固体理论新模式。 理论复杂数十年发展方才完善
经典自由电子论 1900年 德鲁特 量子自由电子论 1927年 索末菲 能带论 1928年 Bloch 1931年 Wilson …… 量子力学基础 保持自由电子观点, 用量子行为约束。 简单直观, 使用方便。 彻底改变观念,放弃自由假定, 建立了固体理论新模式。 理论复杂数十年发展方才完善。 金属导电 理论研究 的发展: