
说明: ★Blakemore:Solid State Physics(1985)一书在晶体结构、晶格振 动之后,以金属中的电子为第3章标题,统一平等的论述了:金属的特征: 经典自由电子论:量子自由电子论;固体的能带:电子运动动力学;超导 等6节。突出了自由电子论在解释金属性质上的历史作用和现实意义,把能 带论和它的关系讲的比较清晰,有利于理解。 ★Kittel;Busch;Omar等人的固体物理教材都是把金属自由电子论 放在能带论之前作为单独一章讲授的,体现了共同的认识。 ★Ashcroft:Solid State Physics更是把自由电子论放在最前面,作 为固体物理的开篇,并由此引入晶体结构,能带论等,突出了自由电子论 在固体理论研究中的历史作用。国内,顾秉林:阎守胜等人的固体物理教 材也采用了这种方式。 固体物理章节安排可能有多种方式,它体现了作者的认识和意图,我 们在学习具体内容的过程中,也要注意从整体上把握好各部分内容之间的 链接,他们之间的相互关系等
说明: ★ Blakemore: Solid State Physics (1985) 一书在晶体结构、晶格振 动之后,以金属中的电子为第3章标题,统一平等的论述了:金属的特征; 经典自由电子论;量子自由电子论;固体的能带;电子运动动力学;超导 等6节。突出了自由电子论在解释金属性质上的历史作用和现实意义,把能 带论和它的关系讲的比较清晰,有利于理解。 ★ Kittel;Busch;Omar 等人的固体物理教材都是把金属自由电子论 放在能带论之前作为单独一章讲授的,体现了共同的认识。 ★ Ashcroft:Solid State Physics 更是把自由电子论放在最前面,作 为固体物理的开篇,并由此引入晶体结构,能带论等,突出了自由电子论 在固体理论研究中的历史作用。国内,顾秉林;阎守胜等人的固体物理教 材也采用了这种方式。 固体物理章节安排可能有多种方式,它体现了作者的认识和意图,我 们在学习具体内容的过程中,也要注意从整体上把握好各部分内容之间的 链接,他们之间的相互关系等

4.2量子自由电子论(Sommerfeld) 一.金属中自由电子的运动状态 二.能态密度 三.基态能量 四.T>OK时电子的分布和能量 既然Dude模型在定性方面是正确的,那么问题的来源就是 不能把电子气看作是经典粒子,不应服从Maxwell--Boltzman经 典统计规律,而应该服从量子统计规律。1927年,Sommerfeld 应用量子力学重新建立了自由电子论,正确地解释了金属的大多 数性质,使自由电子论成为解释金属物理性质的一个方便而直观 的模型。虽然以后能带论以更加严格的数学处理得到了更加完美 的理论结果,但在很多情形下,我们仍然乐于方便地使用自由电 子论来讨论金属问题
4.2 量子自由电子论(Sommerfeld) : 一 . 金属中自由电子的运动状态 二. 能态密度 三. 基态能量 四. T>0K 时电子的分布和能量 既然Drude 模型在定性方面是正确的,那么问题的来源就是 不能把电子气看作是经典粒子,不应服从 Maxwell-Boltzman 经 典统计规律,而应该服从量子统计规律。1927年,Sommerfeld 应用量子力学重新建立了自由电子论,正确地解释了金属的大多 数性质,使自由电子论成为解释金属物理性质的一个方便而直观 的模型。虽然以后能带论以更加严格的数学处理得到了更加完美 的理论结果,但在很多情形下,我们仍然乐于方便地使用自由电 子论来讨论金属问题
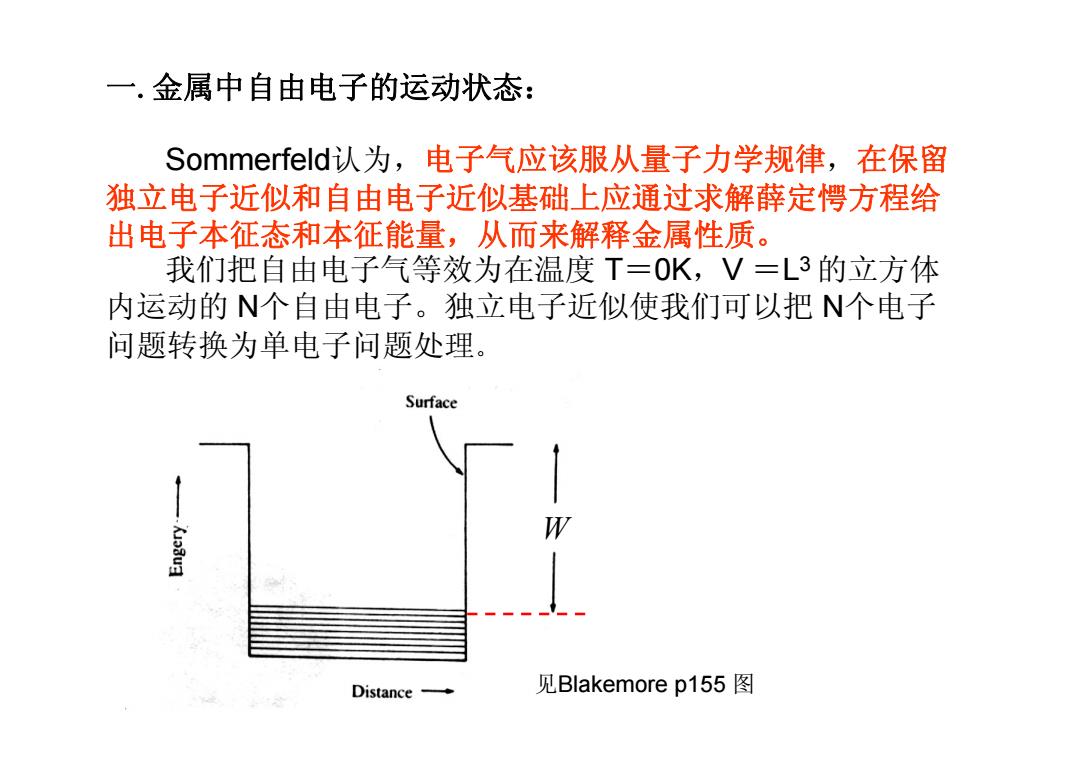
一.金属中自由电子的运动状态: Sommerfeld认为,电子气应该服从量子力学规律,在保留 独立电子近似和自由电子近似基础上应通过求解薛定愕方程给 出电子本征态和本征能量,从而来解释金属性质。 我们把自由电子气等效为在温度T=OK,V=L3的立方体 内运动的N个自由电子。独立电子近似使我们可以把N个电子 问题转换为单电子问题处理。 Surface Xu Distance◆ 见Blakemore p155图
一.金属中自由电子的运动状态: Sommerfeld认为,电子气应该服从量子力学规律,在保留 独立电子近似和自由电子近似基础上应通过求解薛定愕方程给 出电子本征态和本征能量,从而来解释金属性质。 我们把自由电子气等效为在温度 T =0K,V = L3 的立方体 内运动的 N个自由电子。独立电子近似使我们可以把 N个电子 问题转换为单电子问题处理。 见Blakemore p155 图 W

其单电子的运动方程为: v2+V(r)pr)=E0(r) 其中,V()为电子在金属中的势能,8为本征能量,采用 自由电子近似,忽略电子一离子实相互作用,)可取为0。 方程简化为: v2pr)=Ep0 2m 和电子在自由空间的情形一样,其解为平面波: e 2π k二 其中用以标记波函数的k是波矢,它的方向为平面波的传播 方向。将上式代入方程后,得到的电子相应能量为: 方2k2 E(k)= 2m
其单电子的运动方程为: 其中,V(r) 为电子在金属中的势能, 为本征能量,采用 自由电子近似,忽略电子-离子实相互作用, V( r) 可取为 0 。 方程简化为: 2 2 () () () 2 Vr r E r m ϕ ϕ ⎛ ⎞ − ∇+ = ⎜ ⎟ ⎝ ⎠ = 2 2 () () 2 r Er m −∇ = ϕ ϕ = 和电子在自由空间的情形一样,其解为平面波: 1 ( ) ik r k r e V ϕ ⋅ = G G 其中用以标记波函数的 k 是波矢,它的方向为平面波的传播 方向。将上式代入方程后,得到的电子相应能量为: 2 2 ( ) 2 k E k m = = ε 2 k π λ =

由于p(r)同时也是动量算符p=-ihV的本征态: -inver (r)=hker (r) 因而处于p()态的电子具有确定的动量: p=hk 相应的速度: v=卫=k n m 由此,本征能量也可以写成熟悉的经典形式: E= p 1 mv2 2m 2
由于 同时也是动量算符 的本征态: ( ) k ϕ r pˆ = − ∇i = () () k k −i r kr = = ∇ = ϕ ϕ 因而处于 态的电子具有确定的动量 ϕk ( )r : p k = = p k v m m = = = 由此,本征能量也可以写成熟悉的经典形式: 2 1 2 2 2 p E mv m = = 相应的速度: