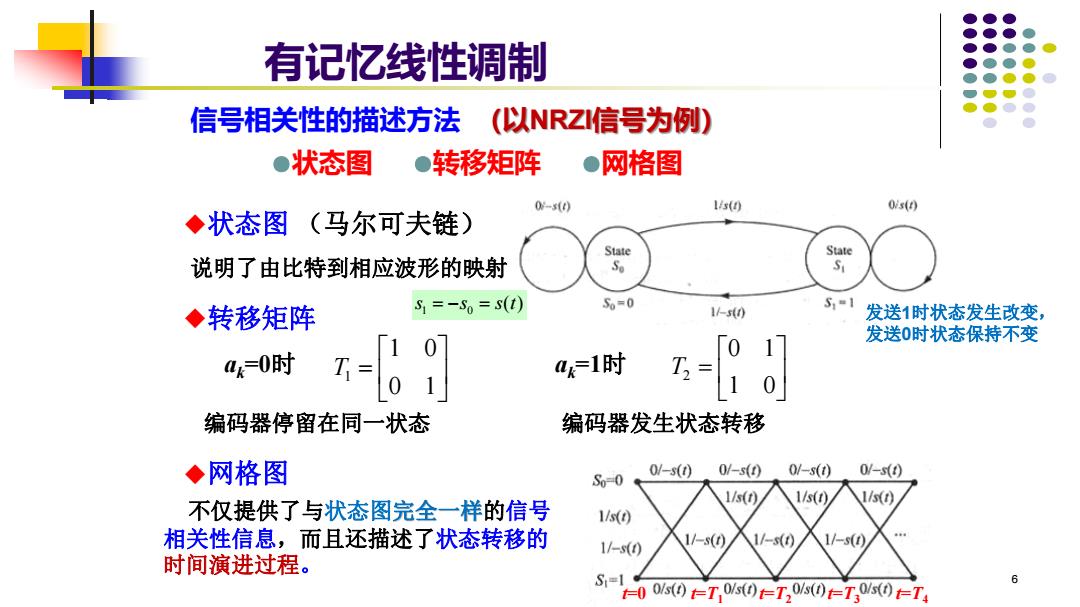
有记忆线性调制 信号相关性的描述方法 (以NRZI信号为例) ●状态图 ●转移矩阵 ●网格图 0-s0 1s0 0s(0 ◆状态图(马尔可夫链) State State 说明了由比特到相应波形的映射 S S1=-S0=s(t) S6=0 ◆转移矩阵 1-s0 发送1时状态发生改变, 发送0时状态保持不变 a=0时 a1时 1 编码器停留在同一状态 编码器发生状态转移 ◆网格图 0/-s() 01-s0 01-s(0 So-0 0/-s(0 l/s(t) 1/s0 不仅提供了与状态图完全一样的信号 1/(0 相关性信息,而且还描述了状态转移的 1/-s(0 1/-s() 1/-s(0 时间演进过程。 S=1 6 00/s0仁T0/s0t=T20/s0eT30Ms0仁T
6 = 0 1 1 0 T1 信号相关性的描述方法 (以NRZI信号为例) ●状态图 ●转移矩阵 ●网格图 ◆状态图 (马尔可夫链) ◆转移矩阵 = 1 0 0 1 T2 ak=0时 ak=1时 编码器停留在同一状态 编码器发生状态转移 ◆网格图 不仅提供了与状态图完全一样的信号 相关性信息,而且还描述了状态转移的 时间演进过程。 有记忆线性调制 说明了由比特到相应波形的映射 1 0 s s s t = − = ( ) t=0 t=T1 t=T2 t=T3 t=T4 发送1时状态发生改变, 发送0时状态保持不变
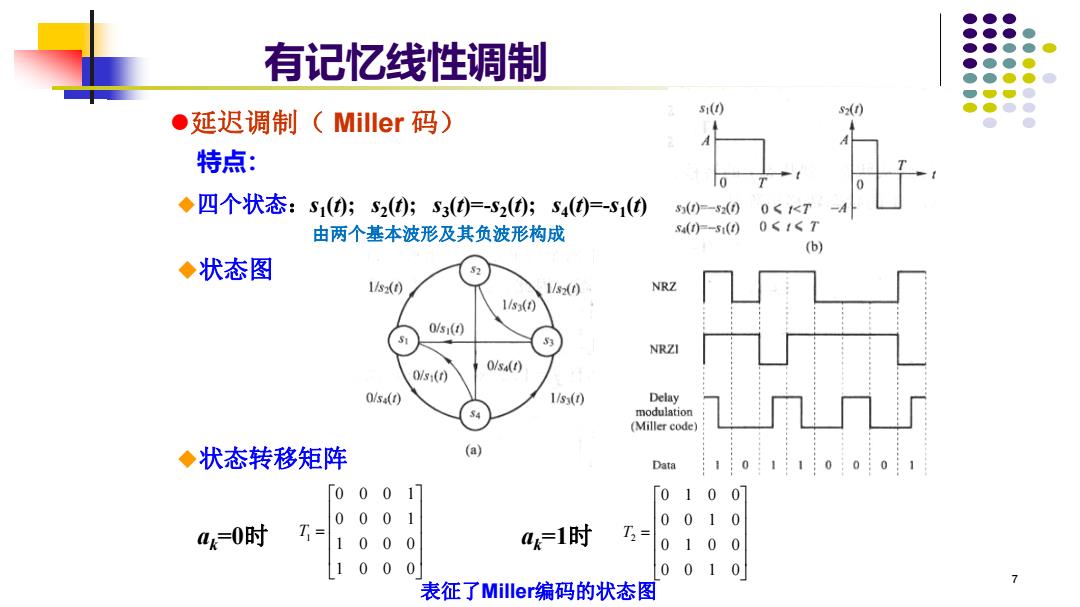
有记忆线性调制 51(0 s2(t) ●延迟调制(Miller码) 特点: ◆四个状态:S1(0;S2();53()F-S2();S4()=-S1() s()-5(00<1K1 由两个基本波形及其负波形构成 b】 ◆状态图 1s(0 1/s0 NRZ 1/s(0 0/51(0 S3 NRZI 0/s4(0 0s:(t) 0/s() 1/s(0 Delay modulation (Miller code】 ◆状态转移矩阵 (a) Data 001] 「0100 0 001 0010 ak=0时 T= 1 00 0 aw=1时 T3= 0100 000 0010 7 表征了Miller编码的状态图
7 = 1 0 0 0 1 0 0 0 0 0 0 1 0 0 0 1 T1 ⚫延迟调制( Miller 码) 特点: ◆四个状态:s1 (t); s2 (t); s3 (t)=-s2 (t); s4 (t)=-s1 (t) ◆状态转移矩阵 = 0 0 1 0 0 1 0 0 0 0 1 0 0 1 0 0 a T2 k=0时 ak=1时 ◆状态图 有记忆线性调制 由两个基本波形及其负波形构成 表征了Miller编码的状态图

有记忆线性调制 有记忆线性调制技术的表征 ●由稳态概率{P,i=1,.K}和转移概率{Pj=1,2,…K} 的k状态马尔科夫链来表征; ●与每一个转移相关联的是一个信号波形s(t)(户1,2,.k) ●转移概率P表示当先前发送信号波形s,(t)之后,发送当前波 形s(t)的概率. ●转移概率矩阵 Bu P2 K Pik P= P2 P2 大 Pak M M P」 转移概率矩阵在确定有记忆数字调制的频谱特性时很有用。 8
8 有记忆线性调制技术的表征 ⚫由稳态概率{ Pi , i =1, …K }和转移概率 { Pij, i, j =1, 2, …K } 的k状态马尔科夫链来表征; ⚫与每一个转移相关联的是一个信号波形sj ( t ) ( j=1, 2, …k ) ⚫转移概率Pij表示当先前发送信号波形si ( t )之后,发送当前波 形sj ( t )的概率. ⚫转移概率矩阵 11 12 1 21 22 2 1 2 k k k k kk p p p p p p P p p p = K K M M L 有记忆线性调制 转移概率矩阵在确定有记忆数字调制的频谱特性时很有用

有记忆非线性调制 有记忆非线性调制 连续相位FSK(CPFSK)和CPM
有记忆非线性调制 连续相位FSK(CPFSK)和CPM 有记忆非线性调制