中国地质大学（武汉）：《信号与系统 Signals and Systems》课程教学资源（课件讲稿）第二章 LTI连续时间系统的时域分析

§2.1系统的数学模型 ·2.LT连续时间系统的状态空间模型 ·例1. 1H YYY xi(t) 12 i2) 2(t)=0.5F i3) 2 y(t 问题(1)y(t)~Vt);(2)x(),X2(t)~V(t) 7

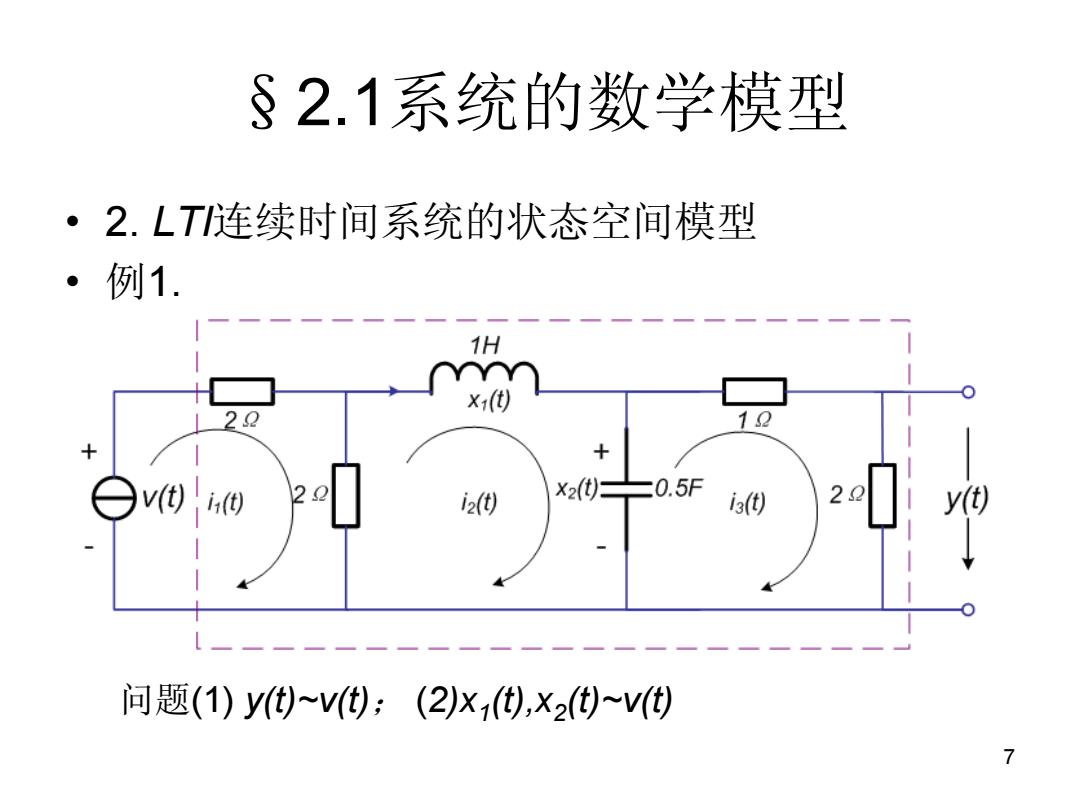
7 §2.1系统的数学模型 • 2. LTI连续时间系统的状态空间模型 • 例1. 问题(1) y(t)~v(t)； (2)x1 (t),x2 (t)~v(t)

§2.1系统的数学模型 -解：v()=4i,()-21,() x()=2(t) ,(0=i,()-i,(0 2 元()+x()+2[3()-()]=0 x2(t)-3i,()=0 y(t)=2i,(t) 8

8 §2.1系统的数学模型 – 解：                                 1 2 1 2 2 2 3 1 2 2 1 2 3 3 4 2 1 2 2 0 3 0 2 v t i t i t x t i t x t i t i t x t x t i t i t x t i t y t i t                             

§2.1系统的数学模型 v(t)…状态方程 -。副周oW者 9

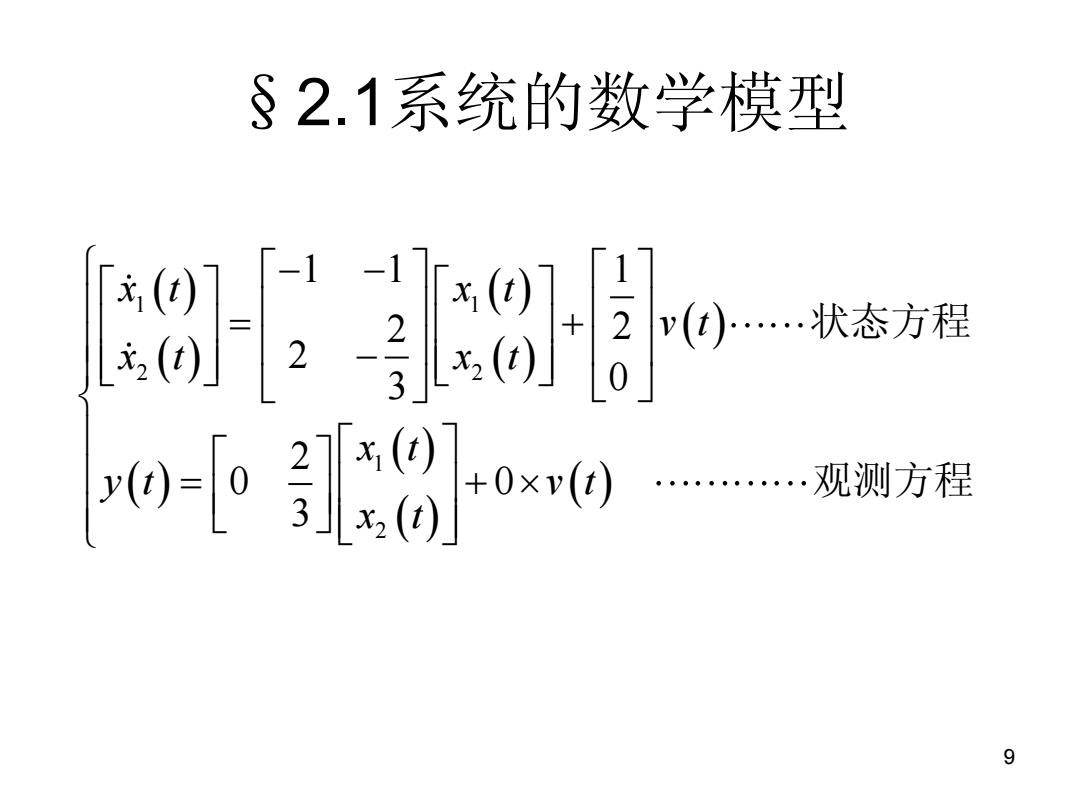
9 §2.1系统的数学模型                   1 1 2 2 1 2 1 1 1 2 2 2 3 0 2 0 0 3 x t x t v t x t x t x t y t v t x t                                                              状态方程 观测方程

§2.1系统的数学模型 v(0 ·状态空间模型 x() m v() n () 输入向量 输出向量 v()= ∈L[t,t]y(t)= ∈Lm[to,ta] y,() y.( x() Γ() 状态向量 状态向量 x(t)= ∈L[,t](t)= ELltozta] x,() 元() 10

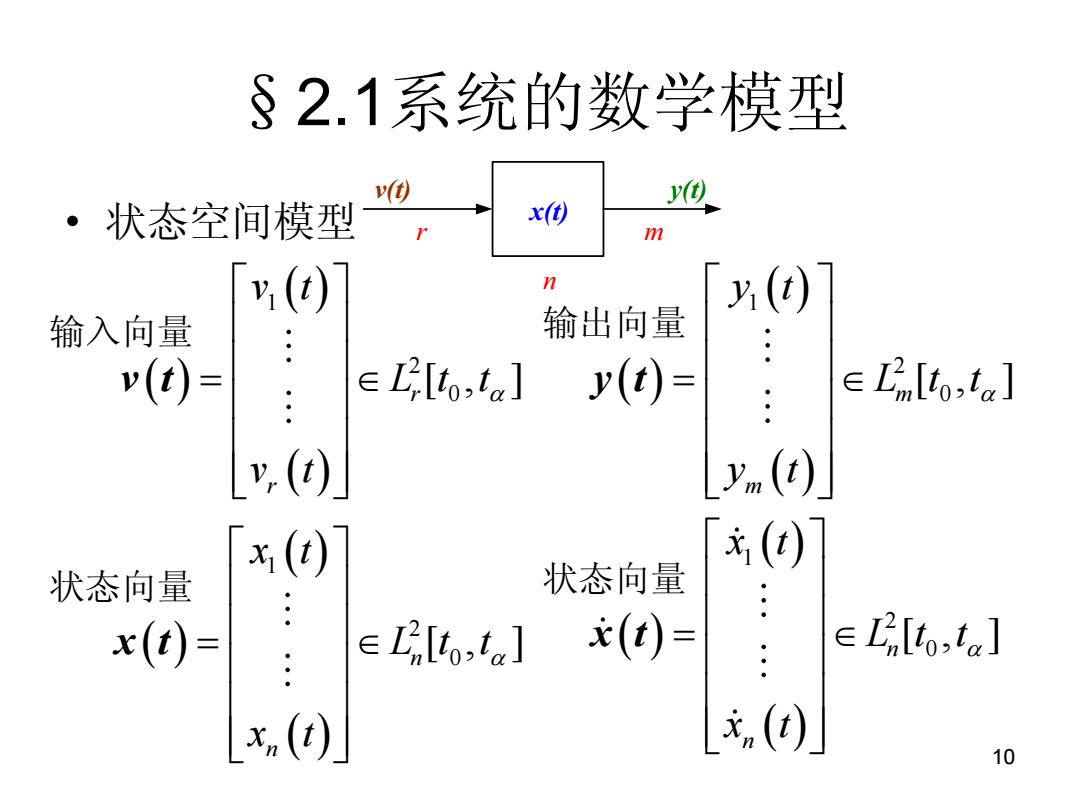
10 §2.1系统的数学模型 • 状态空间模型 v(t) y(t) x(t) r m n       1 2 0 [ , ] r r v t L t t v t                  v t       1 2 0 [ , ] m m y t L t t y t                  y t       1 2 0 [ , ] n n x t L t t x t                  x t       1 2 0 [ , ] n n x t L t t x t                  x t 输入向量 输出向量 状态向量 状态向量

§2.1系统的数学模型 (t)=Axnx(t)+Bny(t)…状态方程 y(t)=Cx(t)+Dxrv(t)..... …观测方程 状态的零输入响应 状态的零状态响应 解 x(t)=e"xo+eMBv(z)dr (t)=Ce*x+[CeB+Do(t-)]v()dr 输出的零输入响应 其中x(t)。=xw 输出的零状态响应 v(t)=v(t)u(t)…因果信号 e=1++4+.=2 11 2

11 §2.1系统的数学模型 • • 解 其中             n n n r m n m r A B C D             状态方程 观测方程 x t x t v t y t x t v t               0 0 t At A t t At A t e e B d Ce Ce B D t d                            0 0 x t x v y t x v         0 2 2 0 1 1 2! ! t At k k k u t e I At A t A x k            因果信号 0 x t x v t v t 状态的零输入响应 状态的零状态响应 输出的零输入响应 输出的零状态响应