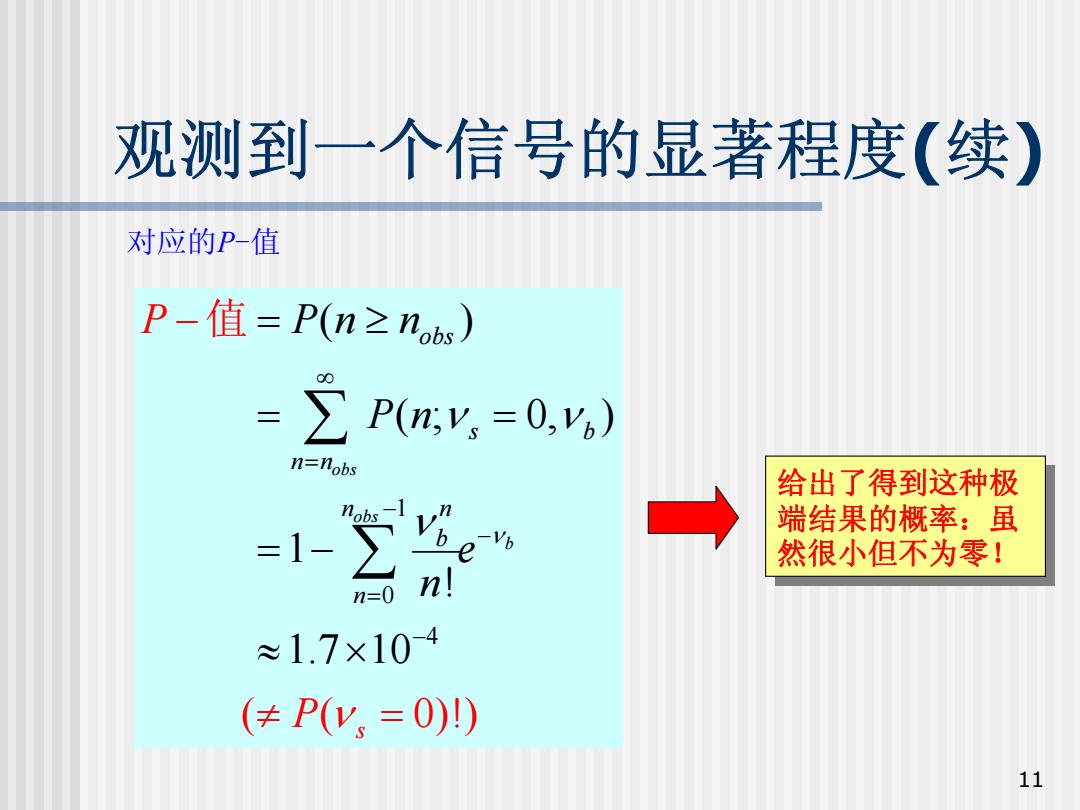
观测到一个信号的显著程度(续) 对应的P值 P-值=P(n≥nbs) =∑P(my,=0,y) n=nobs 给出了得到这种极 nobs 端结果的概率:虽 =1- -Vb 然很小但不为零! n=0 ≈1.7×104 (≠P(y,=0)) 11
11 观测到一个信号的显著程度 ( 续 ) 1 0 4 ( ) ( ; 0, ) 1 ! 1.7 ( ( 0 )!) 10 obs obs b obs s b n n n n b s n P P P n n P n e n ν ν ν ν ν ∞ = − − = − = ≥ = = = ≠ − ≈ × − = ∑ ∑ 值 对应的 P-值 给出了得到这种极 端结果的概率:虽 然很小但不为零! 给出了得到这种极 端结果的概率:虽 然很小但不为零!
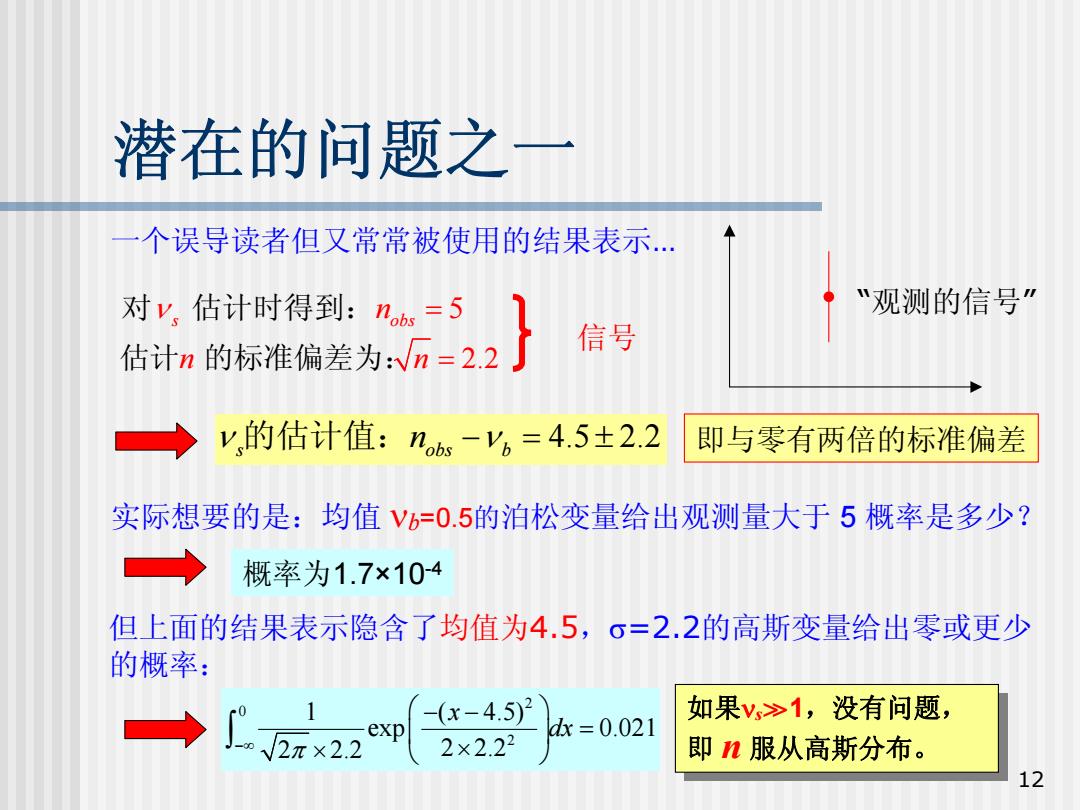
潜在的问题之一 一个误导读者但又常常被使用的结果表示. 对y,估计时得到:ns=5 观测的信号" 估计n的标准偏差为√n=2.2 信号 y,的估计值:ns-y6=4.5±2.2 即与零有两倍的标准偏差 实际想要的是:均值Vb=0.5的泊松变量给出观测量大于5概率是多少? 概率为1.7×104 但上面的结果表示隐含了均值为4.5,σ=2.2的高斯变量给出零或更少 的概率: →222 -x-4.5} 如果V>1,没有问题, 2×22 d=0.021 即n服从高斯分布。 12
12 潜在的问题之一 一个误导读者但又常常被使用的结果表示 … 4.5 2.2 s obs b ν 的估计值: n − ν = ± 信号 即与零有两倍的标准偏差 5 s obs 对 ν 估计时得到: n = 估计n n 的标准偏差为: = 2.2 实际想要的是:均值 ν b=0.5 的泊松变量给出观测量大于 5 概率是多少? 概率为1.7×10-4 但上面的结果表示隐含了均值为4.5,σ=2.2的高斯变量给出零或更少 的概率: “观测的信号 ” 2 0 2 1 ( 4.5 ) e x p 0.021 2 2.2 2 2.2 x dx π −∞ ⎛ ⎞ − − ⎜ ⎟ = × ⎝ ⎠ × ∫ 如果 νsá 1,没有问题, 即 n 服从高斯分布。 如果 νsá 1,没有问题, 即 n 服从高斯分布