
粒子物理与核物理实验中的 数据分析 陈少敏 清华大学 第二讲:常用概率密度函数
粒子物理与核物理实验中的 数据分析 陈少敏 清华大学 第二讲 :常用概率密度函数

本讲要点 口常用的概率密度函数分布的数学形式 ▣相应的平均值与方差 口相关的应用范围
本讲要点 常用的概率密度函数分布的数学形式 相应的平均值与方差 相关的应用范围

二项式分布 N次独立测量,每次只有成功 可以证明其满足 (概率为p)或失败(概率为1-p) 归一化条件 两种可能。得到次成功的概率 N! 为 ∑”pu- N! P(r)= H(W-2P'(I-p)- =[1-p)+p]N=1 方差: 平均值: V[r]=o2 E[r]=4=∑rP(r)=Np =E[(r-4)2] 适用于仪器探 =E[r2]-E2[r] 测效率的计算 Np(1-p)
二项式分布 N 次独立测量,每次只有成功 (概率为 p)或失败(概率为1- p) 两种可能。得到 r次成功的概率 为 r N r p p r N r N P r − − − = ( 1 ) !( )! ! ( ) E [ r ] = = ∑rP ( r ) = Np : μ 平均值 ( 1 ) [ ] [ ] [( ) ] [ ] : 2 2 2 2 Np p E r E r E r V r = − = − = − = μ σ 方差 适用于仪器探 测效率的计算 适用于仪器探 测效率的计算 可以证明其满足 归一化条件 [( 1 ) ] 1 ( 1 ) !( )! ! = − + = − − ∑ − N r r N r p p p p r N r N
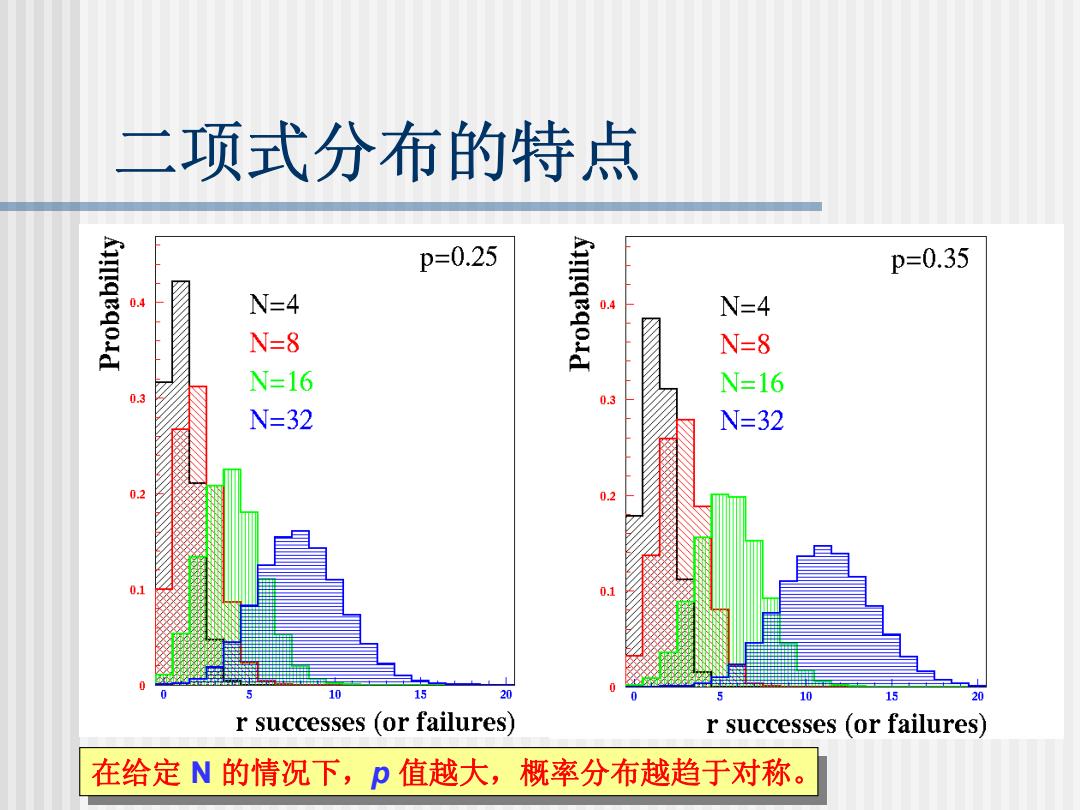
二项式分布的特点 Au!qeqoId p=0.25 p=0.35 0.4 N=4 0.4 N=4 N=8 A!qeqoId N=8 N=-16 N=16 0.3 0.3 N=32 N=32 0.2 0.1 10 15 20 公 r successes (or failures) r successes (or failures) 在给定N的情况下,p值越大,概率分布越趋于对称
二项式分布的特点 在给定 在给定 NN的情况下, 的情况下, pp值越大,概率分布越趋于对称。 值越大,概率分布越趋于对称
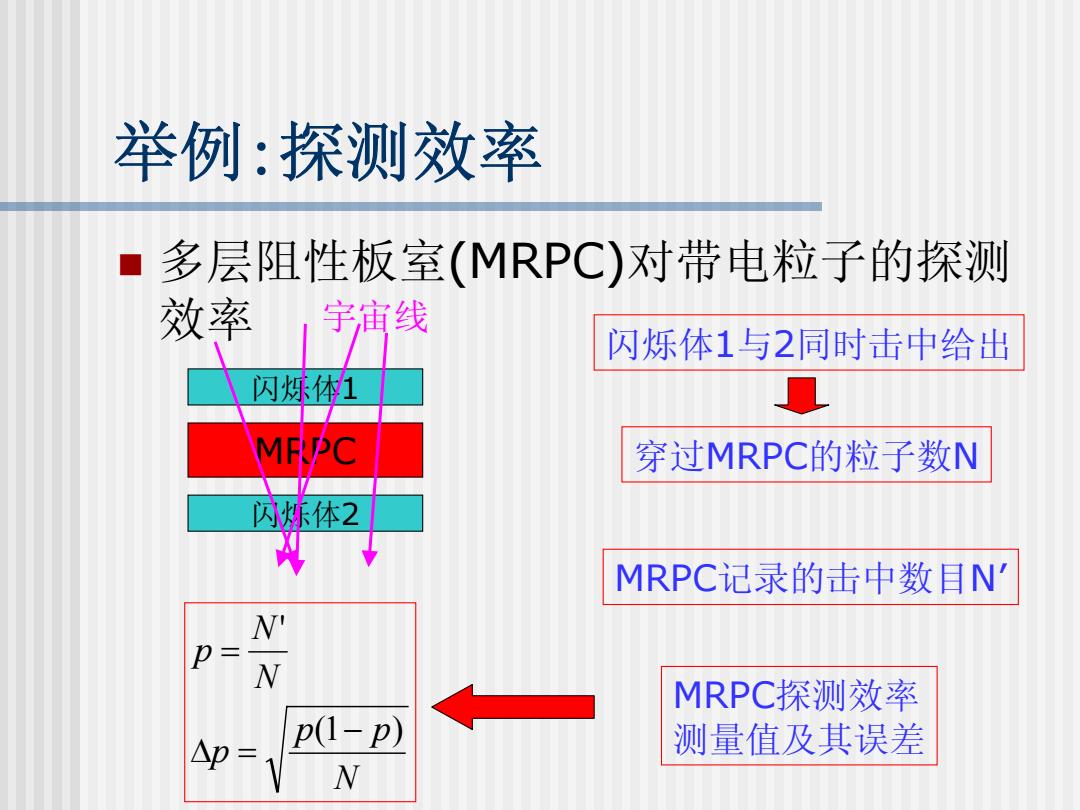
举例:探测效率 多层阻性板室(MRPC)对带电粒子的探测 效率 ,宇庙线 闪烁体1与2同时击中给出 闪烁体1 穿过MRPC的粒子数N 体2 MRPC记录的击中数目N' N p N MRPC探测效率 p(1-p) Ap= 测量值及其误差 N
举例:探测效率 多层阻性板室(MRPC)对带电粒子的探测 效率 闪烁体 1 MRPC 宇宙线 闪烁体 2 闪烁体 1 与 2同时击中给出 穿过MRPC的粒子数 N MRPC记录的击中数目N’ MRPC探测效率 测量值及其误差 N p p p N N p ( 1 ) ' − Δ = =