
粒子物理与核物理实验中的 数据分析 陈少敏 清华大学 第八讲:最大似然法(II) 1
1 粒子物理与核物理实验中的 数据分析 陈少敏 清华大学 第八讲:最大似然法(II)

本讲要点 双参数情况下的最大似然法举例 利用MINUIT数值求解最小值 推广的最大似然法 ■ 利用最大似然法处理分区数据 检验最大似然法的拟合优度 与贝叶斯参数估计之间的关系 2
2 本讲要点 双参数情况下的最大似然法举例 利用MINUIT数值求解最小值 推广的最大似然法 利用最大似然法处理分区数据 检验最大似然法的拟合优度 与贝叶斯参数估计之间的关系

例子:最大似然法处理双参数 考虑散射角分布x=C0SO f(x;a,B)= 1+ax+Bx 2+2B/3 在实际情况下, 探测器也许不可能做全空间探测,即xmn<x<Xmax 这个时候需要考虑效率影响,并对函数进行归一化处理,例如 E效率()= Xmin <X<Xmax 否则 →,f(xa,B)·e(x)dk=1 例如:对于参数为a=0.5,B-0.5,探测器有效范围xmim=-0.95,xmax0.95, 产生n=2000个蒙特卡罗事例,研究用最大似然法处理双参数的问题
3 例子:最大似然法处理双参数 考虑散射角分布 例如:对于参数为α=0.5,β=0.5,探测器有效范围 x min=-0.95, x max= 0.95, 产生 n=2000个蒙特卡罗事例,研究用最大似然法处理双参数的问题。 x = cosθ 2 2 / 3 1 ( ; , ) 2 β α β α β ++ + = x x f x min max 在实际情况下,探测器也许不可能做全空间探测,即 x x < < x 。 这个时候需要考虑效率影响,并对函数进行归一化处理,例如 1 1 f ( ; x x α β, ) ε ( )dx 1 − ⋅ = ∫ θ min max 1 ( ) 0 x x x ε x ⎧ < < = ⎨⎩ 效率 否则
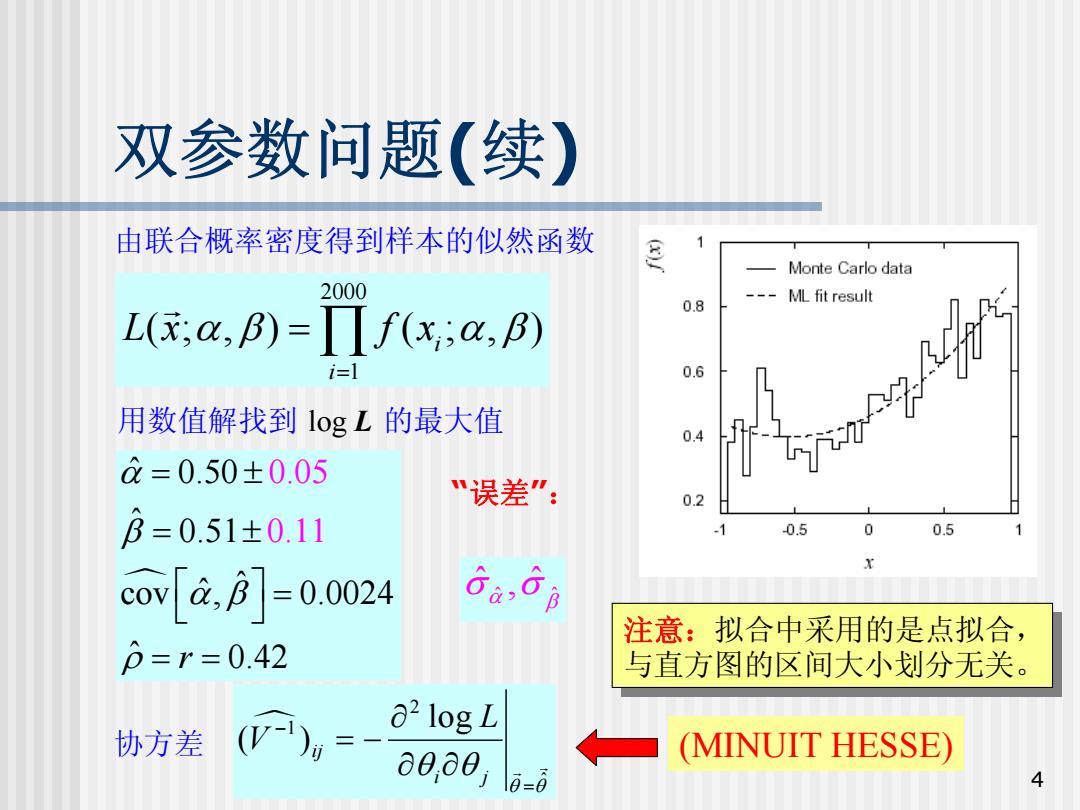
双参数问题(续) 由联合概率密度得到样本的似然函数 Monte Carlo data 2000 0.8 ML fit result L(x;a,B)=f(x;;a,B) i=l 0.6 用数值解找到logL的最大值 04 a=0.50±0.05 "误差” 0.5 B=0.51±0.11 0.5 0.5 X cov[a,B]=0.0024 6 6 注意:拟合中采用的是点拟合, p=r=0.42 与直方图的区间大小划分无关。 () a2 log L 协方差 a0,a0 (MINUIT HESSE) 6=0 4
4 双参数问题 ( 续 ) 用数值解找到 log L 的最大值 m ˆ 0.50 ˆ 0.51 ˆ c o v ˆ, 0.0024 ˆ 0.4 0.05 0.1 2 1 r α β α β ρ = ± = ± ⎡ ⎤ = ⎣ ⎦ = = 协方差 m 2 1 ˆ lo g ( )ij i j L V θ θ θ θ − = ∂ = − ∂ ∂ G G “误差 ”: ˆ ˆ ˆ ˆ , α β σ σ 由联合概率密度得到样本的似然函数 2000 1 ( ; , ) ( ; , ) i i L x α β α f x β = = ∏ G (MINUIT HESSE) 注意:拟合中采用的是点拟合, 与直方图的区间大小划分无关。 注意:拟合中采用的是点拟合, 与直方图的区间大小划分无关
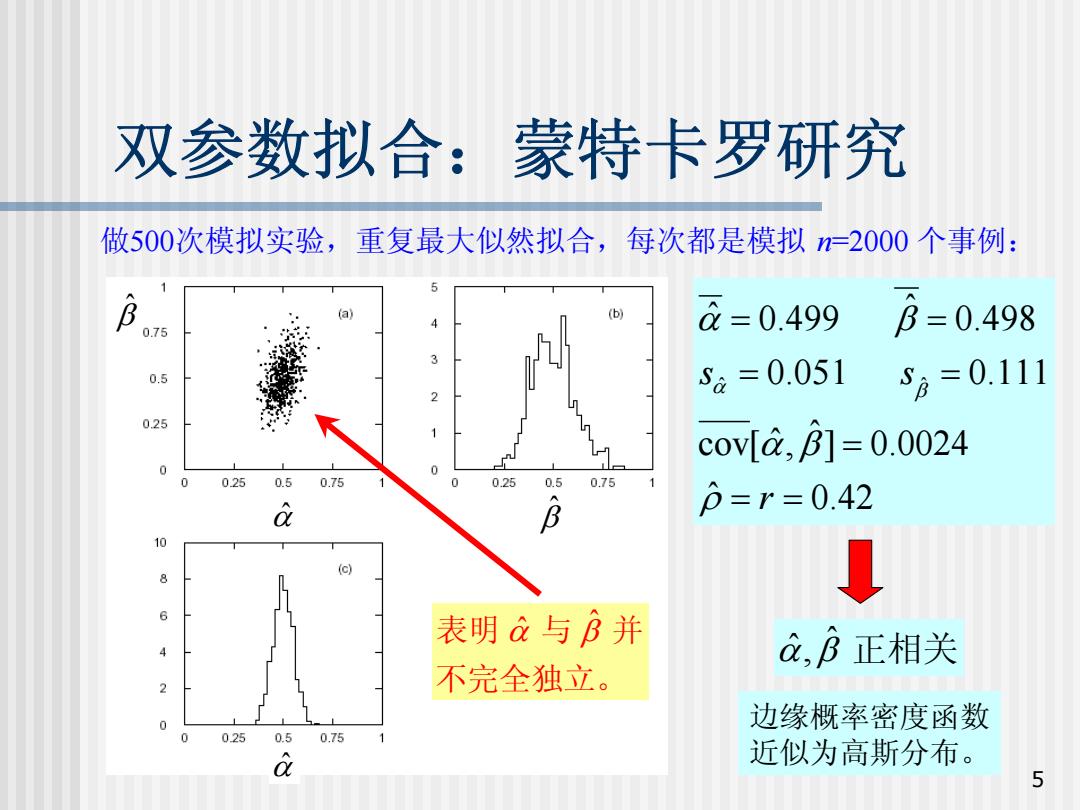
双参数拟合:蒙特卡罗研究 做500次模拟实验,重复最大似然拟合,每次都是模拟=2000个事例: B (a) (b) a=0.499 p=0.498 .75 0.5 s6=0.051 SB=0.111 0.25 cov[a,B]=0.0024 0 025 0.5 0.75 0.25 0.5 0.75 B p=r=0.42 0 (c) 表明a与B并 C,B正相关 不完全独立。 0 边缘概率密度函数 025 0.5 0.75 a 近似为高斯分布。 5
5 双参数拟合:蒙特卡罗研究 做500次模拟实验,重复最大似然拟合,每次都是模拟 n=2000 个事例: ˆ ˆ ˆ ˆ 0.499 0.498 0.051 0.111 ˆ c o v [ ˆ, ] 0.0024 ˆ 0.42 s s r α β α β α β ρ = = = = = = = ˆ α β ˆ, 正相关 边缘概率密度函数 αˆ 近似为高斯分布。 β ˆ αˆ β ˆ ˆ 表明 α β ˆ 与 并 不完全独立