
粒子物理与核物理实验中的数 据分析 陈少敏 清华大学 第三讲:蒙特卡罗方法 http://hep.tsinghua.edu.cn/~chensm/lectures/lecture 3.pdf
粒子物理与核物理实验中的数 据分析 陈少敏 清华大学 第三讲 :蒙特卡罗方法 http://hep.tsinghua.edu.cn/~chensm/lectures/lecture_3.pdf

本讲要点 蒙特卡罗方法 ■随机数产生子 ■任意分布抽样之函数变换法与舍选法 蒙特卡罗方法中的精度问题 ■在粒子与核物理中的应用
本讲要点 蒙特卡罗方法 随机数产生子 任意分布抽样之函数变换法与舍选法 蒙特卡罗方法中的精度问题 在粒子与核物理中的应用

蒙特卡罗方法简介 蒙特卡罗方法就是利用一系列随机数来计算各种概率和相关 量的数值分析技术。通常的步骤为: 1)产生一系列在[0,1]之间均匀分布的随机数,,,'m。 2) 利用这些随机数按某些概率密度函数∫(x)抽样生成我 们感兴趣的另一随机序列x,x2,,X,0 3) 利用这些x值来估计∫(x)的一些特性,例如:通过找 到在区间a≤x≤b的x比例, 给出积分值fx)dk。 第一层面上的应用: 蒙特卡罗计算=积分 第二层面上的应用: 蒙特卡罗变量=“模拟的数据
蒙特卡罗方法简介 蒙特卡罗方法就是利用一系列随机数来计算各种概率和相关 量的数值分析技术。通常的步骤为: 1) 产生一系列在[0,1]之间均匀分布的随机数 。 2) 利用这些随机数按某些概率密度函数 抽样生成我 们感兴趣的另一随机序列 。 3) 利用这些 值来估计 的一些特性,例如:通过找 到在区间 的 比例,给出积分值 。 m r ,r ,..., r 1 2 f ( x ) n x , x ,..., x 1 2 x x f ( x ) a ≤ x ≤ b ∫ b a f ( x )dx 第一层面上的应用: 蒙特卡罗计算 = 积分 第二层面上的应用: 蒙特卡罗变量 = “模拟的数据
随机数 用物理方法产生 用数学方法产生 真正的随机数 伪随机数 不可重复 可以重复 产生速度慢 产生的速度快
随机数 用物理方法产生 真正的随机数 不可重复 产生速度慢 用数学方法产生 伪随机数 可以重复 产生的速度快
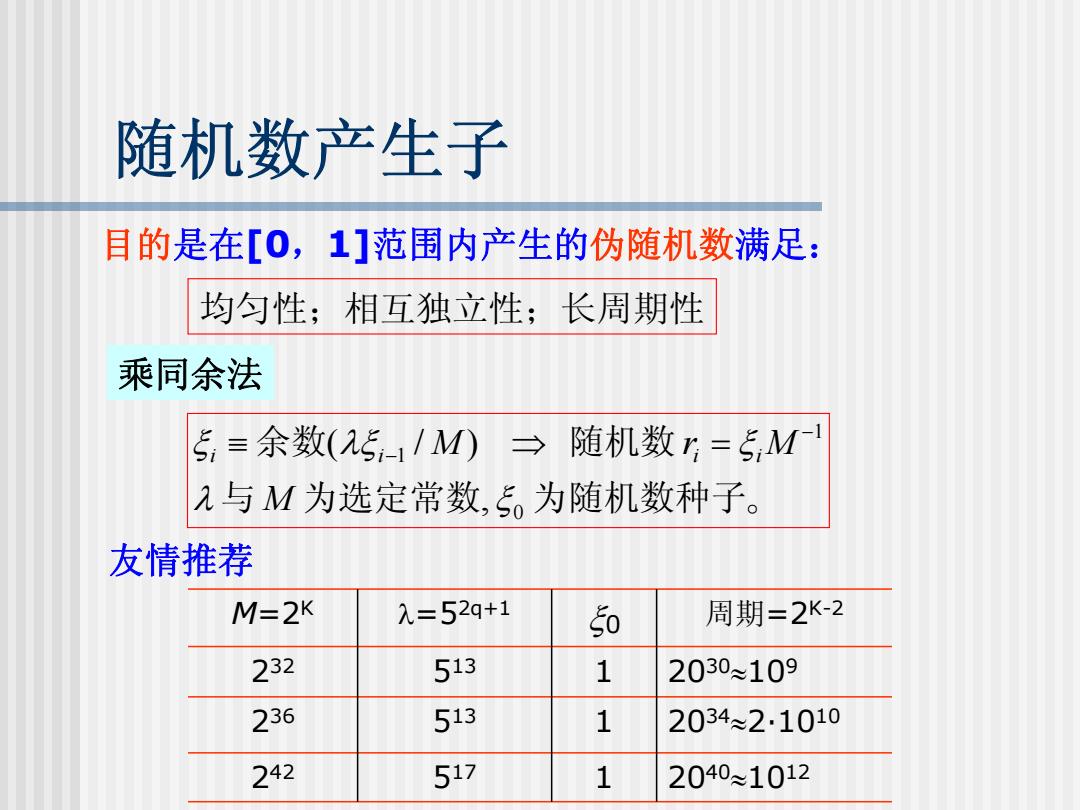
随机数产生子 目的是在[0,1]范围内产生的伪随机数满足: 均匀性;相互独立性;长周期性 乘同余法 5=余数(5,-1/M)→随机数5=5M 入与M为选定常数,5。为随机数种子。 友情推荐 M=2K λ=52q+1 50 周期=2K-2 232 513 1 2030≈109 236 53 1 2034≈2.1010 242 517 1 2040≈1012
随机数产生子 目的是在[0 ,1]范围内产生的伪随机数满足: 均匀性;相互独立性;长周期性 乘同余法 , 。 ( / ) 0 1 1 与 为选定常数 为随机数种子 余数 随机数 λ ξ ξ λξ ξ M i i M ri i M − ≡ − ⇒ = 友情推荐 M=2 K λ=52q+1 ξ0 周期=2K-2 232 513 1 2030 ≈10 9 236 513 1 2034 ≈2·1010 242 517 1 2040 ≈1012