中国地质大学（武汉）：《信号与系统 Signals and Systems》课程教学资源（课件讲稿）第四章 信号的谱表示

§4.2典型周期信号的谱 0 02w f0)=a,+∑a,cos0r n= Et a a 2=n0 T 菲f0esat 02o T ) 0n= a. 020 22

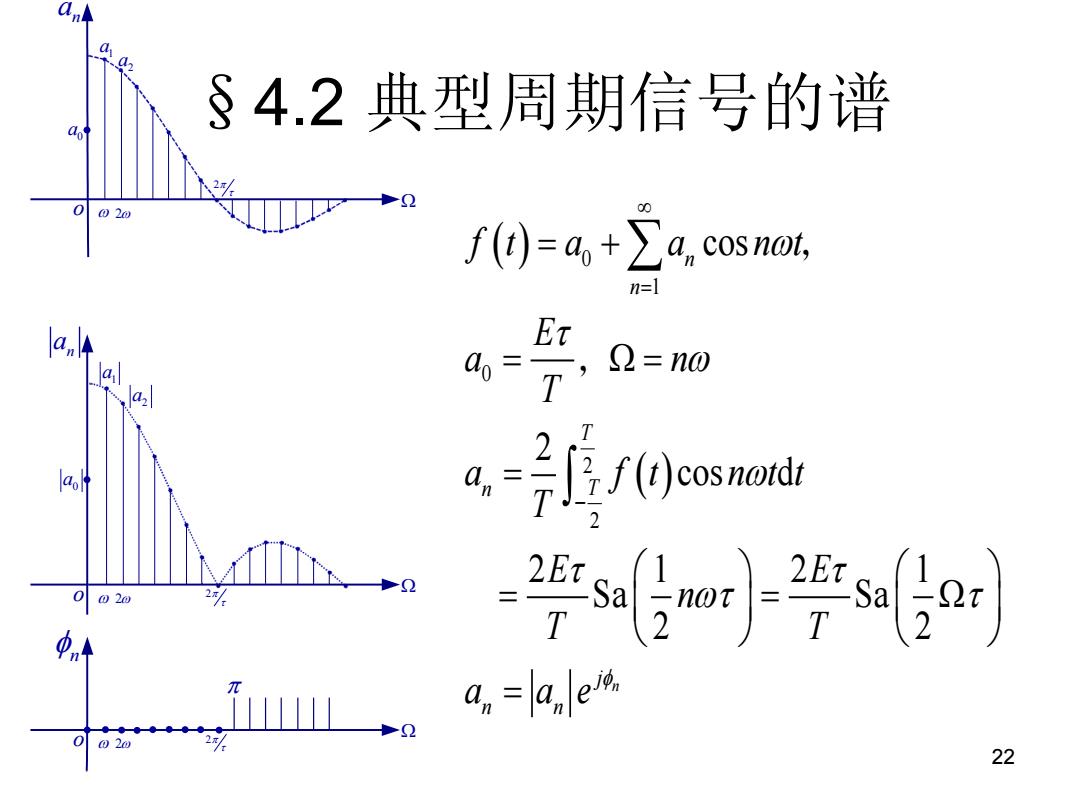
22 o 2  0 a 1 a 2 a  n a  2 o 2  0 a 1 a 2 a  n a  2 o 2    2 n  §4.2 典型周期信号的谱     0 1 0 2 2 cos 2 cos d 2 1 2 1 Sa Sa 2 2 n n n T n T j n n f t a a n t E a n T a f t n t t T E E n T T a a e                                     ，

§4.2典型周期信号的谱 ·（)f)的频谱为可列的无穷多条线谱 ·(2)谱线间隔为0 27元 ·(3)线谱包络为san: ·(4)0到第一零点之间的谱线的个数： [2][表示对取粉 23

23 §4.2 典型周期信号的谱 • (1) f(t)的频谱为可列的无穷多条线谱 • (2)谱线间隔为 • (3)线谱包络为 • (4) 0到第一零点之间的谱线的个数： （ 表示对 取整) 2 T    1 Sa 2         2  T                T        T 

§4.3(-o,∞)上函数的傅里叶变换 ·1.问题提出 虑[k6+]→(-+o= T-→o0, 则 -7」fe)e→0 T→0 谱线间隔： 2π 0= →0，T>0 T 此时信号有周期信号变为非周期信号，其频谱由 离散谱变为连续谱。 24

24 §4.3 上函数的傅里叶变换 • 1.问题提出 考虑 则 谱线间隔： 此时信号有周期信号变为非周期信号，其频谱由 离散谱变为连续谱。   1 L ,         1 1 0 0 0 2 j 2 L , L , , , , 2 1 lim lim d 0 T n t n T T T T t t T t T F f t e t T                 令 2 0,T T      

§4.3L(-oo,∞)上函数的傅里叶变换 ImF,T=mj反f)ed →li 0→ 2xE.mo）-f(0emd 其中，(o) 表示单位频率上的谱强度， 0 F(o)=lim 2πFnnw） 为孔t)的频谱密度函数（谱 0→0 密度) 。 令：2=no→F(2)=f(t)edt 25

25 §4.3 上函数的傅里叶变换 其中， 表示单位频率上的谱强度， 为 f(t) 的频谱密度函数（谱 密度）。 令：   1 L ,         2 j 2 j 0 lim lim d 2 lim d T n t n T T T n n t F T f t e t F n f t e t                    F n n        0 2 lim F n n F            j d t n F f t e t           

§4.3L(-oo,o)上函数的傅里叶变换 ·2.傅里叶变换 -定义：对f()∈L(-o,∞)，则 傅里叶（正）变换： F(@)=F(f(t)=f(t)e-imdr 傅里叶反变换： f()-FF)()edo"F) 其中：F(o)=F(o)eo为f(t)的（频谱（密度） F(o)为f(t)的幅度谱（密度），(o)为f(t)的相位谱（密度） 6

26 §4.3 上函数的傅里叶变换 • 2.傅里叶变换 – 定义：对 傅里叶(正)变换： 傅里叶反变换：   1 L ,      1     f t L , ,则        j d t F f t f t e t         F          2 1 j j 1 d d 2 f t t f t F F e F e f                     F     j   F F e f t( )      为 的(频)谱(密度) F f t f t     为 ( ) ( ) 的幅度谱(密度),  为 的相位谱(密度) 其中：