中国地质大学（武汉）：《信号与系统 Signals and Systems》课程教学资源（课件讲稿）第四章 信号的谱表示

§4.1L[o,t。]上的傅里叶级数 ·8.能量定理 对f(0eL[6,+T小，有"f()fd=2ET 17

17 §4.1 上的傅里叶级数 • 8.能量定理   1 L , 0 t t       0 0 2 2 2 L , d 0 0 t T n t n f t t t T f t t F T    对    ，有 

§4.1L[,t]上的傅里叶级数 ·9.均方收敛性（依范数收敛，强收敛） -定理（均方收敛）：对f(t)∈L[,t+T,则 -fo-立re dr=0 其中(t)=f(t)-∑Feine为误差， 7r)-立re dt为均方误差。 一在个别点，甚至零测度集上不收敛不影响均方收敛性。 一2N+1项F.S.近似，欧式范数最小方差最小均方差 最小。 → 18

18 §4.1 上的傅里叶级数 • 9.均方收敛性（依范数收敛，强收敛） – 定理（均方收敛）：对 其中 – 在个别点，甚至零测度集上不收敛不影响均方收敛性。 – 2N+1项F.S.近似，欧式范数最小 方差最小 均方差 最小。   1 L , 0 t t     2 L , , 0 0    f t t t T 则   0 0 2 1 j lim d 0 N t T n t n N t n N f t F e t T                0 0 j 2 1 j d n t n n N t T n t n t n N t f t F e f t F e t T               为误差， 为均方误差。  

§4.1L[o,t。]上的傅里叶级数 ·10.可F.S.展开的充分条件 一定理（可F.S.展开的充分条件）： 若f(t)∈L[o,t+T],则F<o。 证明：r=于了”f()e心d lFa≤(le =77f(h=7/(e儿s∞ max≤元f(rl 19

19 §4.1 上的傅里叶级数 • 10.可F.S.展开的充分条件 – 定理（可F.S.展开的充分条件）： 若 证明：   1 L , 0 t t     1 L , 0 0 n      f t t t T F ，则 。           0 0 0 0 0 0 -j -j 1 1 1 d 1 d 1 1 d 1 max t T n t n t t T n t n t t T t n n F f t e t T F f t e t T f t t f t T T F f t T                

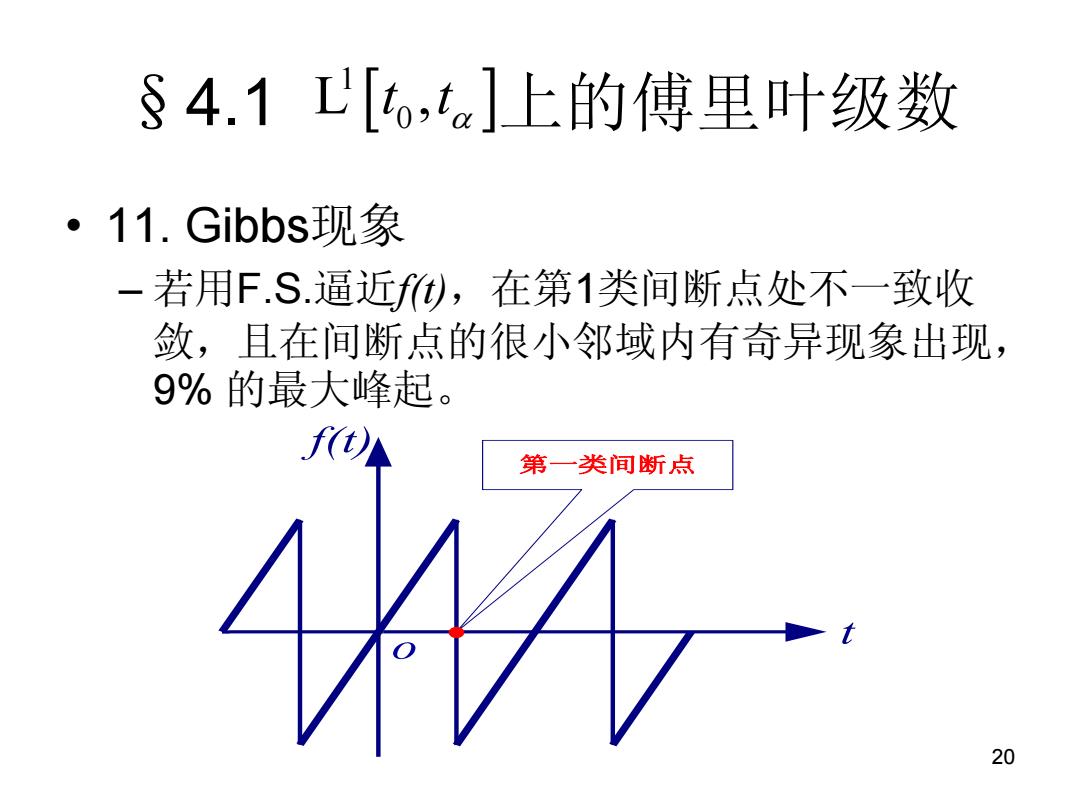
§4.1工[，t]上的傅里叶级数 ·11.Gibbs现象 -若用F.S.逼近f,在第1类间断点处不一致收 敛，且在间断点的很小邻域内有奇异现象出现， 9%的最大峰起 ft)A 第一类间断点 20

20 §4.1 上的傅里叶级数 • 11. Gibbs现象 – 若用F.S.逼近f(t)，在第1类间断点处不一致收 敛，且在间断点的很小邻域内有奇异现象出现， 9% 的最大峰起。   1 L , 0 t t o f(t) t 第一类间断点

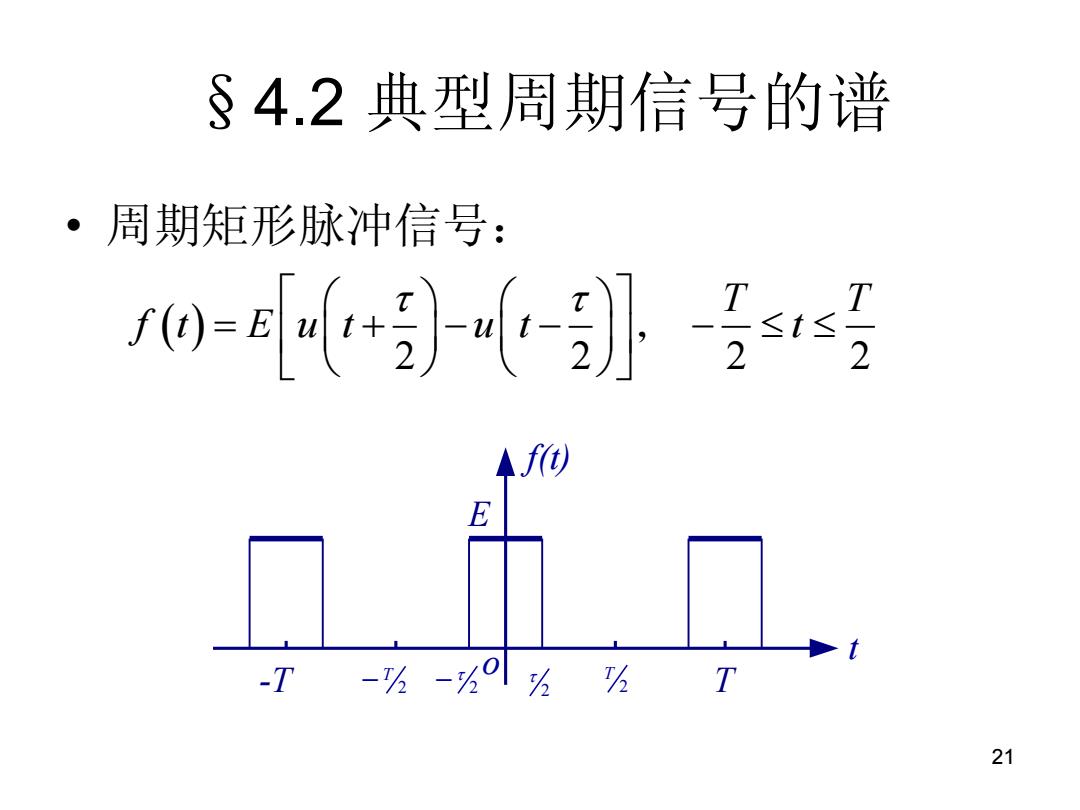
§4.2典型周期信号的谱 ·周期矩形脉冲信号： 0-引 T t≤ T-2 ◆f E -T-为-⅓个为hT 21

21 §4.2 典型周期信号的谱 • 周期矩形脉冲信号：   2 2 2 2 T T f t E u t u t t                            ， f(t) t o E -T 2 T T 2  T 2  2 