中国地质大学（武汉）：《信号与系统 Signals and Systems》课程教学资源（课件讲稿）第四章 信号的谱表示

§4.3L(-oo,o)上函数的傅里叶变换 -定义：F{f()}存在：F(o<∞ 一定理： F{f()存在的充分条件： 对f()∈L(-∞，∞)，F{f(t)}存在。 27

27 §4.3 上函数的傅里叶变换 – 定义： – 定理： 存在的充分条件：   1 L ,   F  f t F  存在:    F  f t         1 对    f t f t L , , F 存在

§4.3L(-o,∞)上函数的傅里叶变换 -F:L(-o0,+∞)→L(-0,+∞)映射 -f(t)=FF()=F(@)edy f()∈L[o,4。+T],f()=Femo, (f(t),=f(t)e-icdt (f(),e）=(2zJnF(o)edw,e》 =J2元JF(o)e"ddt =JF(o)2元Jrea-rdt do 6()=2元Jedt→=JF(o)δ(o-21o=F() 令2o,有F(o)=f(t)e2d

28 §4.3 上函数的傅里叶变换 – 映射 –   1 L ,       1 : L , L ,  F             1 j d t f t F F e f          F                           1 j 0 0 j j j j j + j -j - + j - + - L , , , , d 1 , d , 2 1 d dt 2 1 dt d 2 d n t n n t t t t t t t t f t t t T f t F e f t e f t e t f t e F e e F e e F e F F                                                                       1 j dt 2 t e              j , dt F f t e t          令 有 

§4.3L(-o,∞)上函数的傅里叶变换 -d=olo-) (enwr,em）=T6nm eyck,6+7o= 2π 而eo王L(-0,+oo）,0∈(-o0,+0) 29

29 §4.3 上函数的傅里叶变换 –   1 L ,             j j j j j j j 2 0 0 j 2 1 , d 2 , , 2 L , , , L , , , t t t t n t m t mn n t n t e e e e t e e T e t t T T e                                    而

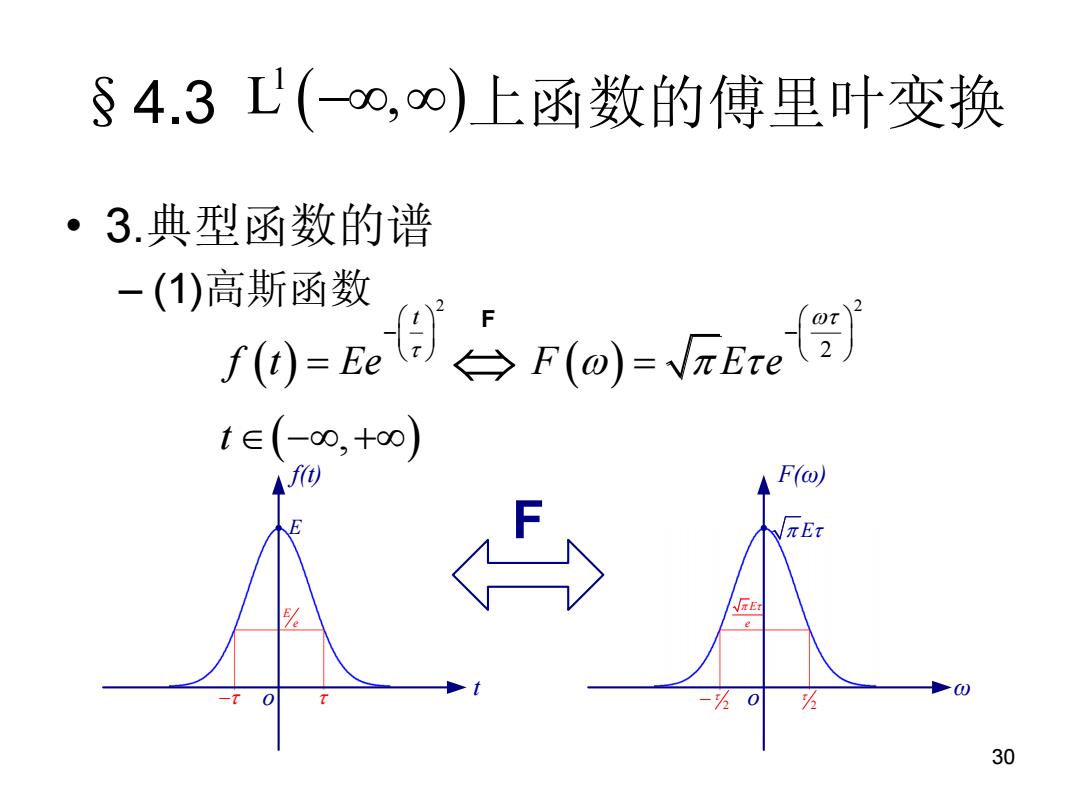
§4.3L(-o,∞)上函数的傅里叶变换 ·3.典型函数的谱 -（1)高斯函数 /0-e日ro=FEe t∈(-oo,+oo） NπEx FE红 e 30

30 §4.3 上函数的傅里叶变换 • 3.典型函数的谱 – (1)高斯函数   1 L ,         2 2 2 , t f t Ee F E e t                          F t E o f(t)   E e ω o F(ω) 2  2  E e   F  E

§4.3L(-oo,∞)上函数的傅里叶变换 高斯函数：exp(-ar2) - - 高斯函数为正实函数 一高斯函数的傅里叶变换仍是高斯的 一高斯函数是速降函数 -令B=L=元0=2/ e2 F <>e-ir2 31

31 §4.3 上函数的傅里叶变换 – 高斯函数： – 高斯函数为正实函数 – 高斯函数的傅里叶变换仍是高斯的 – 高斯函数是速降函数 – 令   1 L ,    2 exp ax 1 E f 1, , 2        2 2 t f e e      F