
时问常数 函数表示式中e的指数项(-t/RC)是无量纲的,因此R 和C的乘积具有时间的量纲,通常以来表示,称为时 间常数。 必 当C用法拉、R用欧姆为单位时,RC的单位为秒,这 是因为:欧法=欧库/伏=欧安秒/伏=欧秒欧=秒。 电压、电流衰减的快慢取决于时间常数的大小。 RC电路的零输入响应是由电容的初始电压U,和时间 常数x=RC所确定。 11
时间常数 ❖ 函数表示式中e的指数项(-t/RC) 是无量纲的,因此R 和C的乘积具有时间的量纲,通常以来表示,称为时 间常数。 ❖ 当C用法拉、R用欧姆为单位时,RC的单位为秒,这 是因为:欧·法=欧·库/伏=欧·安·秒/伏=欧·秒/欧=秒。 ❖ 电压、电流衰减的快慢取决于时间常数的大小。 ❖ RC电路的零输入响应是由电容的初始电压U0和时间 常数 =RC所确定。 11
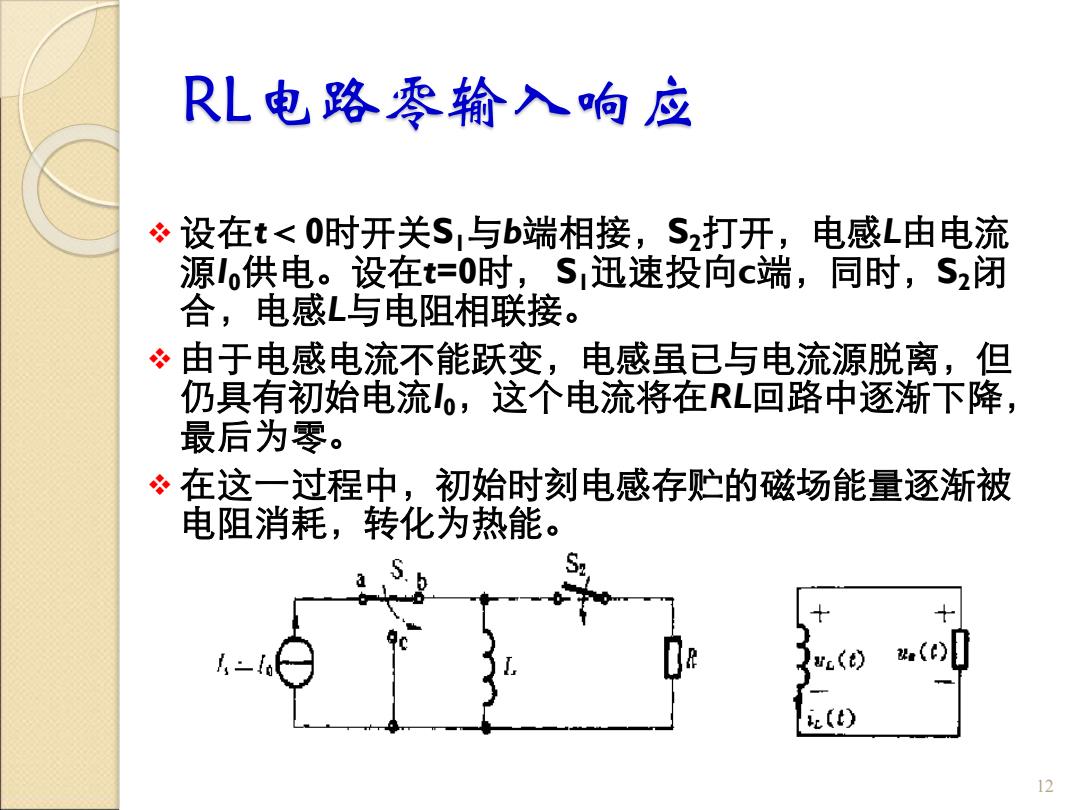
RL电路零输入响应 设在t<0时开关S,与b端相接,S2打开,电感L由电流 源lo供电。设在t=0时,S,迅速投向c端,同时,S2闭 合,电感L与电阻相联接。 ”由于电感电流不能跃变,电感虽已与电流源脱离,但 仍具有初始电流l0,这个电流将在RL回路中逐渐下降, 最后为零。 在这一过程中,初始时刻电感存贮的磁场能量逐渐被 电阻消耗,转化为热能。 i(t) 12
RL电路零输入响应 ❖ 设在t<0时开关S1与b端相接,S2打开,电感L由电流 源I0供电。设在t=0时, S1迅速投向c端,同时,S2闭 合,电感L与电阻相联接。 ❖ 由于电感电流不能跃变,电感虽已与电流源脱离,但 仍具有初始电流I0,这个电流将在RL回路中逐渐下降, 最后为零。 ❖ 在这一过程中,初始时刻电感存贮的磁场能量逐渐被 电阻消耗,转化为热能。 12
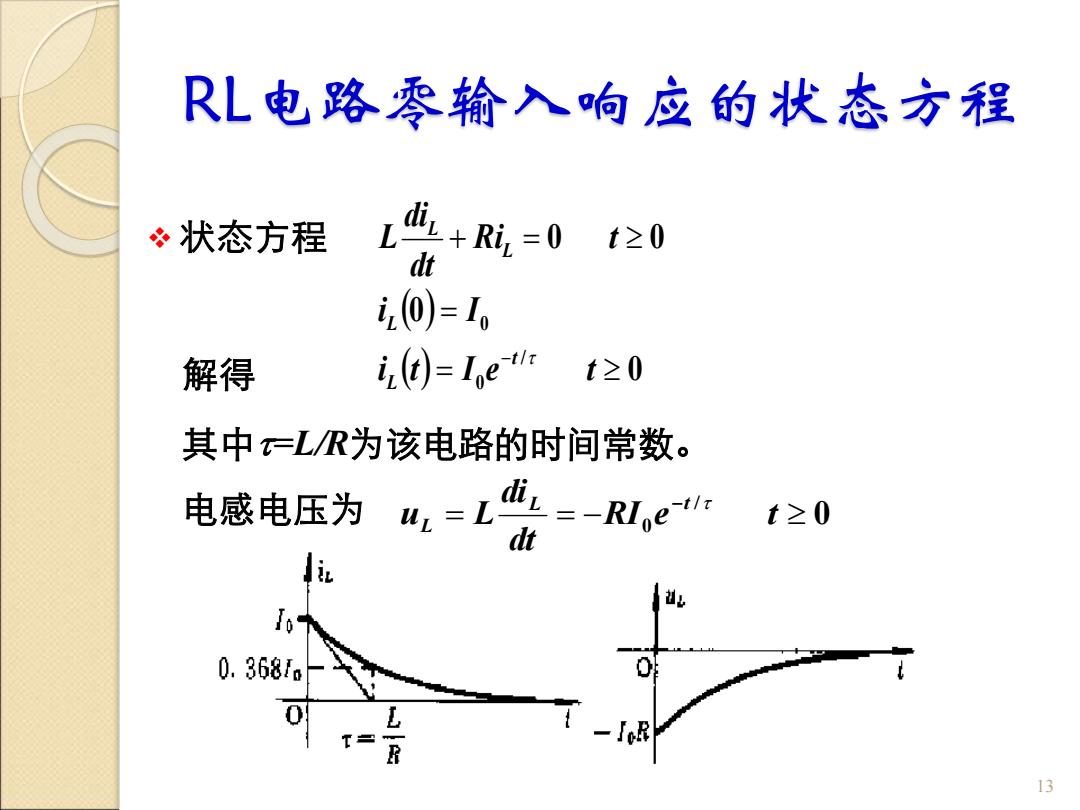
RL电路零输入响应的状态方程 必状态方程 Ldit +Ri,-0 t≥0 dt i,0)=1o 解得 i(t)=Ie t≥0 其中二LR为该电路的时间常数。 电感电压为“,L房= t≥0 0.36810 0 T 13
RL电路零输入响应的状态方程 ❖ 状态方程 13 解得 其中=L/R为该电路的时间常数。 电感电压为 ( ) ( ) 0 0 0 0 / 0 0 = = + = − i t I e t i I Ri t dt di L t L L L L 0 / = = − 0 − RI e t dt di u L L t L

结论 零输入响应是在输入为零时,由非零初始状态产生的, 它取决于电路的初始状态和电路特性。 ÷在求解时,首先求电容电压或电感电流的初始值,对 一 阶电路来说,电路特性为时间常数x。 不论是RC电路还是RL电路,零输入响应都是随时间 按指数规律衰减的,在没有外施电源的条件下,原有 的贮能逐渐衰减到零。 在RC电路中,电容电压uc总是由初始值uc(O)单调地 衰减到零,时间常数RC;在RL电路中,i总是由初 始值(0)单调地衰减到零,其时间常数=LR。 特征根具有时间倒数或频率的量纲,故称为固有频率。 在电路理论中固有频率用来表明网络的固有性质。 14
结论 ❖ 零输入响应是在输入为零时,由非零初始状态产生的, 它取决于电路的初始状态和电路特性。 ❖ 在求解时,首先求电容电压或电感电流的初始值,对 一阶电路来说,电路特性为时间常数。 ❖ 不论是RC电路还是RL电路,零输入响应都是随时间 按指数规律衰减的,在没有外施电源的条件下,原有 的贮能逐渐衰减到零。 ❖ 在RC电路中,电容电压uC总是由初始值uC(0)单调地 衰减到零,时间常数=RC;在RL电路中,iL总是由初 始值iL (0)单调地衰减到零,其时间常数=L/R。 ❖ 特征根具有时间倒数或频率的量纲,故称为固有频率。 在电路理论中固有频率用来表明网络的固有性质。 14
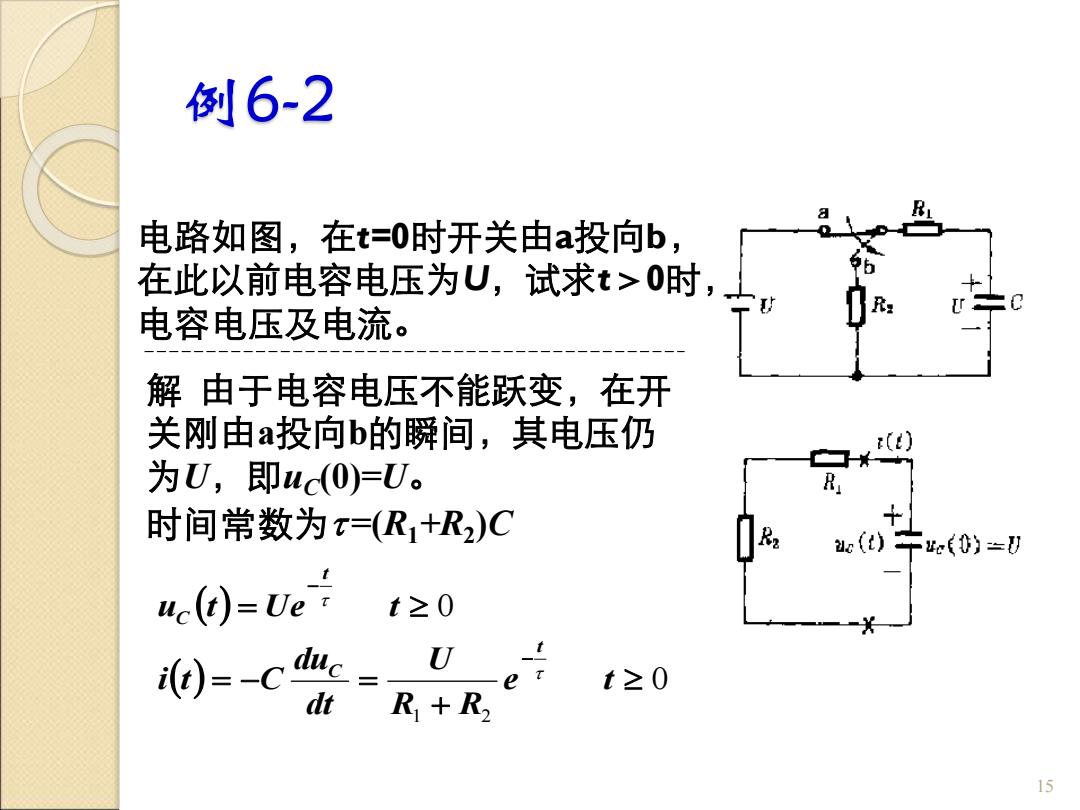
例6-2 电路如图,在t=0时开关由a投向b, 在此以前电容电压为U,试求t>0时,, 电容电压及电流。 解由于电容电压不能跃变,在开 关刚由a投向b的瞬间,其电压仍 () 为U,即uc(O)=U。 时间常数为=(R+R2)C c(t)e0)=U uc(t)=Ve t≥0 0=c duc= U =R1+R e t≥0 15
例6-2 电路如图,在t=0时开关由a投向b, 在此以前电容电压为U,试求t>0时, 电容电压及电流。 15 解 由于电容电压不能跃变,在开 关刚由a投向b的瞬间,其电压仍 为U,即uC(0)=U。 时间常数为 =(R1+R2 )C ( ) ( ) 0 0 1 2 + = − = = − − e t R R U dt du i t C u t U e t t C t C