
方法(2) 若对线性系统在初始状态为零时输入单位脉冲函数,单 位脉冲响应的形式于零输入响应形式相同。所以当单位 脉冲响应趋于零时,系统则稳定。 综上所述,系统稳定的充要条件:系统的全部特征跟 都具有负实部。即系统传递函数的全部极点均位于[s] 平面的左半平面,系统则稳定
方法(2) 若对线性系统在初始状态为零时输入单位脉冲函数,单 位脉冲响应的形式于零输入响应形式相同。所以当单位 脉冲响应趋于零时,系统则稳定。 s t n i i i A e D s M s w t L G s L = − − = = = 1 1 1 ] ( ) ( ) ( ) [ ( )] [ 综上所述,系统稳定的充要条件:系统的全部特征跟 都具有负实部。即系统传递函数的全部极点均位于[s] 平面的左半平面,系统则稳定
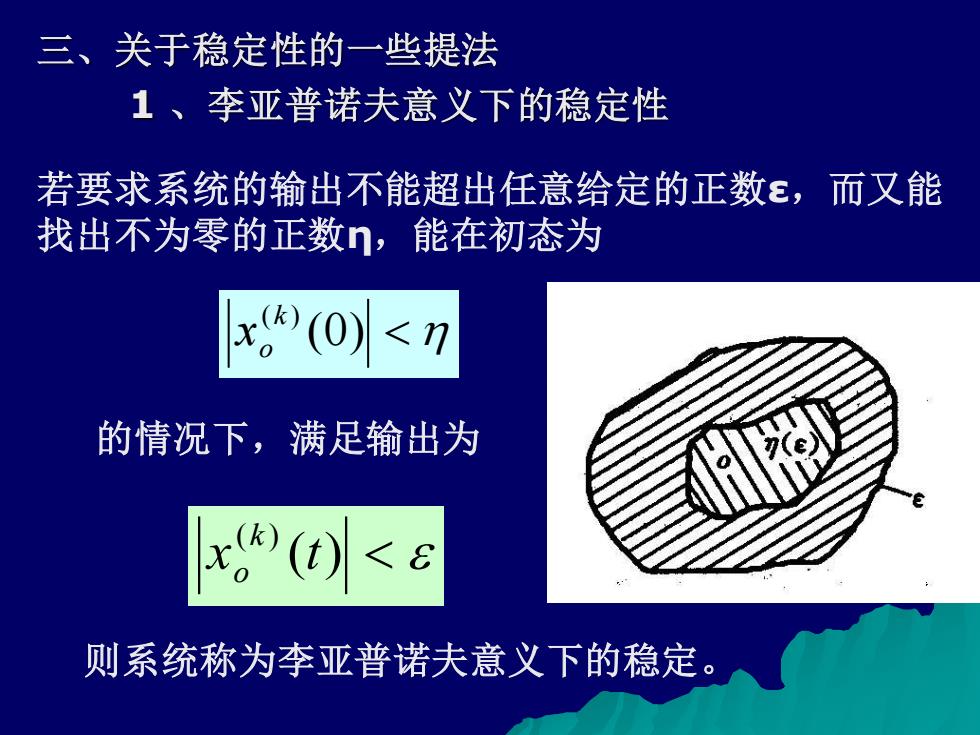
三、关于稳定性的一些提法 1、李亚普诺夫意义下的稳定性 若要求系统的输出不能超出任意给定的正数E,而又能 找出不为零的正数n,能在初态为 x(0)<7 的情况下,满足输出为 x(t)<a 则系统称为李亚普诺夫意义下的稳定
三、关于稳定性的一些提法 1 、李亚普诺夫意义下的稳定性 若要求系统的输出不能超出任意给定的正数ε,而又能 找出不为零的正数η,能在初态为 (0) (k ) o x 的情况下,满足输出为 ( ) ( ) x t k o 则系统称为李亚普诺夫意义下的稳定

2、渐近稳定性 渐近稳定就是线性系统稳定性的定义。系统若是渐近 稳定,就一定是李亚普诺夫意义下的稳定,反之不然。 3、“小偏差”稳定性 “小偏差”稳定性又称“局部稳定性”。系统一般都 具有非线性,在小范围内系统是稳定的,在大范围 内系统就不一定稳定
2 、渐近稳定性 3、 “小偏差”稳定性 渐近稳定就是线性系统稳定性的定义。系统若是渐近 稳定,就一定是李亚普诺夫意义下的稳定,反之不然。 “小偏差”稳定性又称“局部稳定性”。系统一般都 具有非线性,在小范围内系统是稳定的,在大范围 内系统就不一定稳定

§5.2 Routh(劳斯)稳定判据 一、系统稳定的必要条件 D(s)=ans”+an-1s"+.+a,s+a,=0 +an-ls+.+ s”+ a5+0=(s-5s-52)s-3) a an an -0-6-)=r-位r1+(2s,+-8 0 an-2 an i=1,j=2 i<i
§5.2 Routh(劳斯)稳定判据 一、 系统稳定的必要条件 i n i n n n i j i j i j n n n i i n n i n i n n n i j i j i j n n i i n n n n n n n n n n n n n s a a s s a a s a a s s s s s s s s s s s s s s s s s s s a a s a a s a a s D s a s a s a s a 1 0 1, 2 2 1 1 1 2 1, 2 1 1 1 2 1 2 1 1 1 0 1 0 1 1 ( 1) ( ) ( ) ( )( ) ( ) ( ) ( ) ( 1) ( )( ) ( ) ( ) 0 = = = − = − = − = = − = − − − − = − = = − − − − = − + − + − + + + + = − − − = + + + + =

要使全部特征根均具有负实部,必须满足两 个条件,即必要条件: 1)特征方程的各项系数ai都不为零。因为 若有一系数为零,则必出现实部为零的特 征根或实部有正有负的特征根,此时系统 为临界稳定或不稳定。 2)特征方程的各项系数ai的符号都相同
要使全部特征根均具有负实部,必须满足两 个条件,即必要条件: 1)特征方程的各项系数ai都不为零。因为 若有一系数为零,则必出现实部为零的特 征根或实部有正有负的特征根,此时系统 为临界稳定或不稳定。 2)特征方程的各项系数ai的符号都相同