
(2)设选出的连续三点是P,P,Pk,则向量 PP与PP的夹角a的绝对值,应大于某 个预先给定的限制阈值ao°,若小于a 则不应选取而应考虑是能将P,至P和 P;至Pk两段合并。 P Pk
(2)设选出的连续三点是Pi ,Pj ,Pk ,则向量 Pi Pj与Pj Pk的夹角α的绝对值,应大于某 个预先给定的限制阈值α0。,若小于α0 , 则Pj不应选取而应考虑是否能将Pi至Pj和 Pj至Pk两段合并
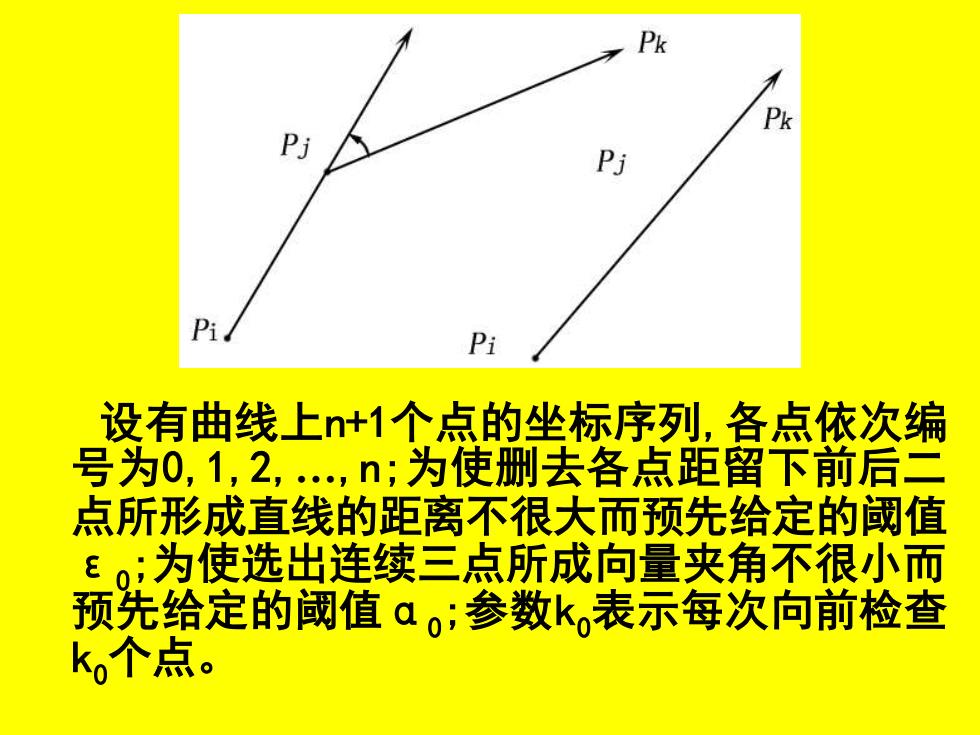
Pk Pi 设有曲线上+1个点的坐标序列,各点依次编 号为0,1,2,,n;为使删去各点距留下前后二 点所形成直线的距离不很大而预先给定的阈值 ε。:为使选出连续三点所成向量夹角不很小而 预先给定的阈值αo:参数k,表示每次向前检查 k个点
设有曲线上n+1个点的坐标序列,各点依次编 号为0,1,2,…,n;为使删去各点距留下前后二 点所形成直线的距离不很大而预先给定的阈值 ε0 ;为使选出连续三点所成向量夹角不很小而 预先给定的阈值α0 ;参数k0表示每次向前检查 k0个点

1.〔初始化)i←0,j←0,k←ko输出点编号 0,s←1。{i记最近己选之点,初始起点0为必 选,j记待检查之点,算法中保持i≤j,待检查 线是点到k的直线。} 2.〔共线性检查〕检查点到k间各点共线性。 若不能通过,距离直线PP最远的点是m,则 k←m返回本步开头。否则继续。{本步必能通 过,因最坏在k=j+1时能通过。} 3.〔暂定j前后两线方向)L2←点到k的方向, 若i=j则L1←L2,到6;否则继续。L2是暂定找 到从向后的新线方向,L1是前次找到原有线 方向。}
1.〔初始化〕 i←0,j←0,k←k0 ,输出点编号 0,s←1。{i记最近己选之点,初始起点0为必 选,j记待检查之点,算法中保持i≤j,待检查 线是点j到k的直线。} 2.〔共线性检查〕检查点j到k间各点共线性。 若不能通过,距离直线Pj Pk最远的点是m,则 k←m返回本步开头。否则继续。{本步必能通 过,因最坏在k=j+1时能通过。} 3.〔暂定j前后两线方向〕L2←点j到k的方向, 若i=j则L1←L2,到6;否则继续。{L2是暂定找 到从j向后的新线方向,L1是前次找到原有线 方向。}

4.〔向量夹角检查〕检查P,P,Pk三点形成 二向量L1和L2的夹角的绝对值,若可以通 过即应发生合并,做j←i然后返2,否则继 续。{本步检查通过即点j不能选取,而要 检查原i到k的直线。} 5.〔找到一个选取点)i←j,L1←点j到k的 方向,输出点编号j,s←s+1。 6.〔准备下次)j←k,k←k+ko,若k>n则k←n, 若j≤n-1则返2,否则继续。 7.〔最后取点)输出点编号n,算法结束
4.〔向量夹角检查〕检查Pi ,Pj ,Pk三点形成 二向量L1和L2的夹角的绝对值,若可以通 过即应发生合并,做j←i然后返2,否则继 续。{本步检查通过即点j不能选取,而要 检查原i到k的直线。} 5.〔找到一个选取点〕i←j,L1←点j到k的 方向,输出点编号j,s←s+1。 6.〔准备下次〕j←k,k←k+k0 ,若k>n则k←n, 若j≤n-1则返2,否则继续。 7.〔最后取点〕输出点编号n,算法结束
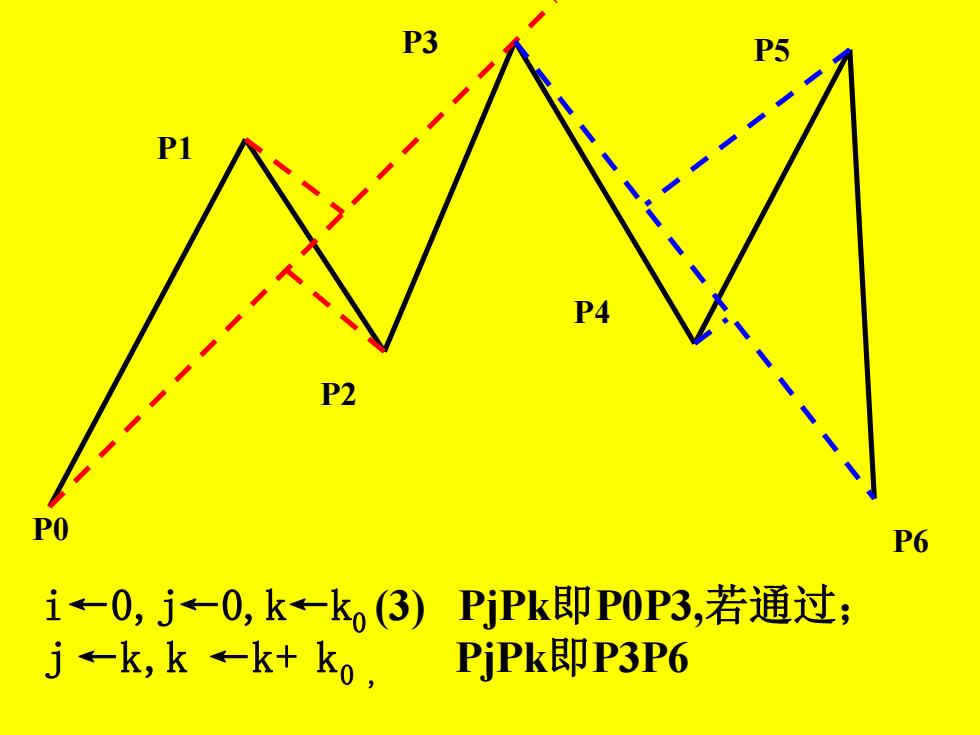
P2 PO P6 i←0,j←0,k←k(3) PPk即P0P3,若通过; j-k,k←k+k0, PPk即P3P6
P0 P1 P2 P3 P4 P5 P6 i←0,j←0,k←k0 (3) PjPk即P0P3,若通过; j ←k,k ←k+ k0 , PjPk即P3P6