
不明确问题检验方法 所有多边形按顶点最大z坐标值 排序后得到一个排序表,设P是排在 表中最后的那个多边形。 设Q是排在P前面并且z坐标范围 与其发生交迭的一个多边形,对Q与 P的次序关系进行检查
不明确问题检验方法 所有多边形按顶点最大z坐标值 排序后得到一个排序表,设P是排在 表中最后的那个多边形。 设Q是排在P前面并且z坐标范围 与其发生交迭的一个多边形,对Q与 P的次序关系进行检查

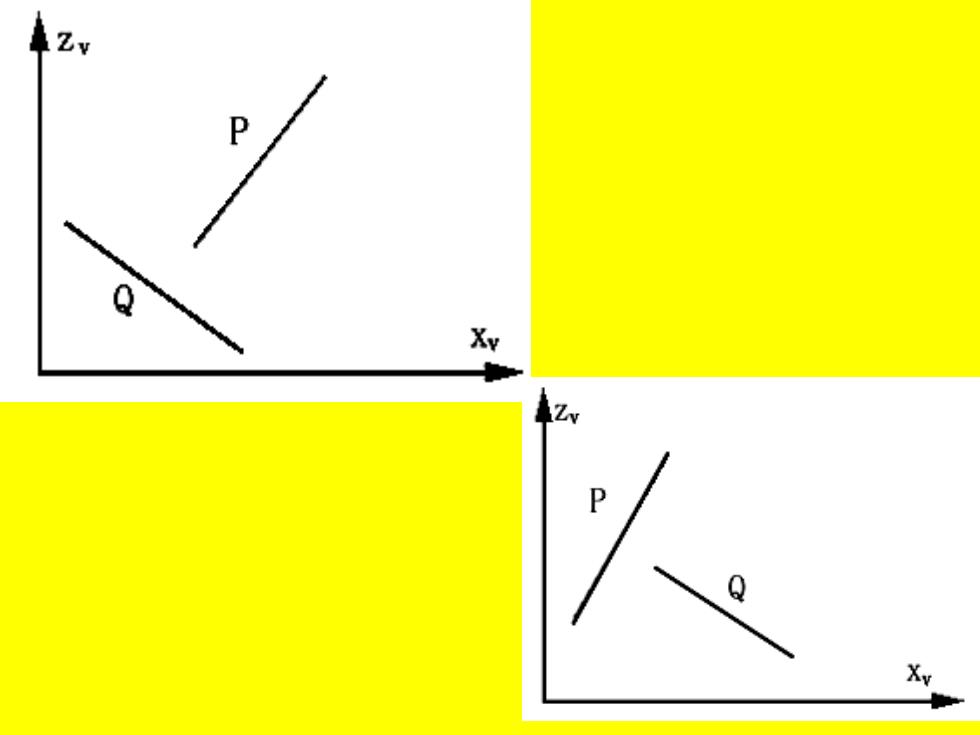
检查可以按下面列出的五个步 骤进行,每个步骤判断一种情况。 1.多边形的x坐标范围不相交迭,所以 多边形不相交迭。 2.多边形的y坐标范围不相交迭,所以 多边形不相交迭。 3.P整个在Q远离观察点的一侧。 4. Q整个在P的靠近观察点的一侧。 5.多边形在z=0平面上的投影本身不相 交迭
检查可以按下面列出的五个步 骤进行,每个步骤判断一种情况。 1.多边形的x坐标范围不相交迭,所以 多边形不相交迭。 2.多边形的y坐标范围不相交迭,所以 多边形不相交迭。 3. P整个在Q远离观察点的一侧。 4. Q整个在P的靠近观察点的一侧。 5. 多边形在z=0平面上的投影本身不相 交迭
Xy

如果所有这五步检查都为假,就假 定P是遮挡了Q,交换P和Q在排序表中 的位置。 如果仍做交换,算法会永远循环 下去而没有结果。 为了避免循环,可以做一个限制 当做过首次五步检查后,发生某个多 边形被移到排序表的末尾时,就立即 加上一个标记,以后就不能再做移动。 出现再次应该移动时,用一个多边形
如果所有这五步检查都为假,就假 定P是遮挡了Q,交换P和Q在排序表中 的位置。 如果仍做交换,算法会永远循环 下去而没有结果。 为了避免循环,可以做一个限制。 当做过首次五步检查后,发生某个多 边形被移到排序表的末尾时,就立即 加上一个标记,以后就不能再做移动。 出现再次应该移动时,用一个多边形
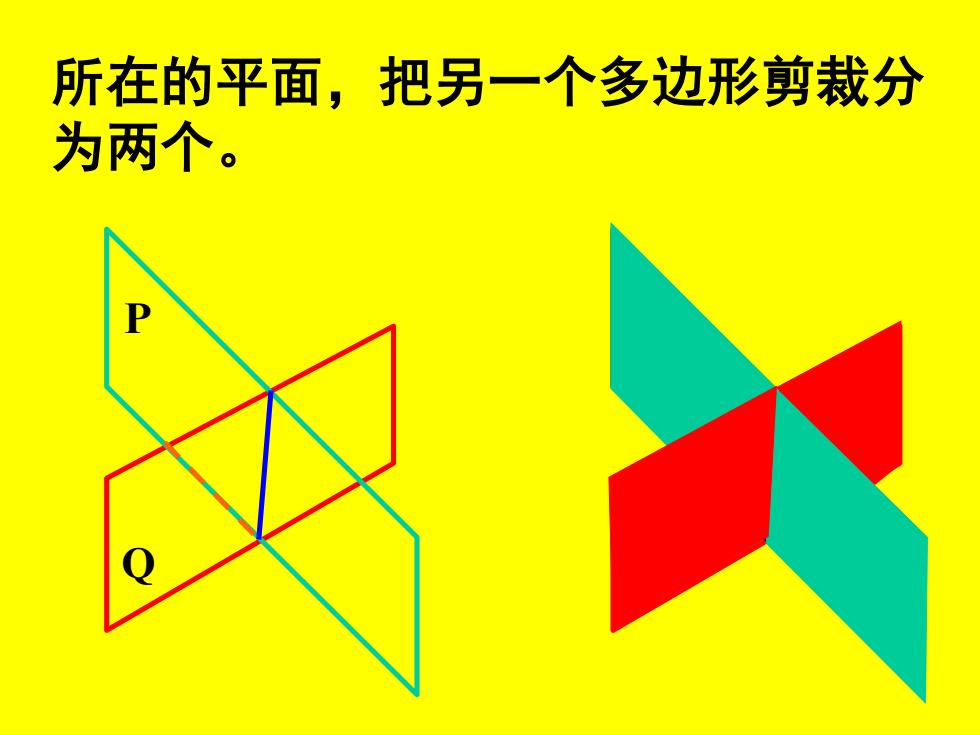
所在的平面,把另一个多边形剪裁分 为两个
所在的平面,把另一个多边形剪裁分 为两个。 P Q