
两线段AB和CD交点的算法 1.〔计算行列式〕△←(x。-×)(y。y)-(x。 xa(y。y 若△=0,则两线段重合或平行,可算做无交 点,算法结束; 2.〔计算交点参数〕人←(x。×)y。y) (x。-xy。ya)/△ 若入<0或入>1,则无交点,算法结束; u←(x。-×)(y。ya)-(x。-x)(y。ya)/△ 若K0或4>1,则无交点,算法结束;
两线段AB和CD交点的算法 1.〔计算行列式〕 ←(xb -xa )(yc -yd )-(xc - xd )(yb -ya) 若 =0,则两线段重合或平行,可算做无交 点,算法结束; 2.〔计算交点参数〕 ←((xc -xa )(yc -yd )- (xc -xd )(yc -ya ))/ 若 <0或 >1,则无交点,算法结束; ←((xb -xa )(yc -ya )-(xc -xa )(yb -ya ))/ 若 <0或 >1,则无交点,算法结束; λ λ λ

3.〔计算交点〕x←x+入(x。×),y←y+入y。 ya),输出交点(x,y)后算法结束; 多条线段求交 寻找这样的算法,其计算工作量要大体 上与交点个数成正比,即只对有可能相交 的两线段计算交点,对不可能相交的线段 不计算交点,使算法有更好的效率
3.〔计算交点〕x←xa + (xb -xa ),y←ya + (yb - ya ),输出交点(x,y)后算法结束; λ λ 多条线段求交 寻找这样的算法,其计算工作量要大体 上与交点个数成正比,即只对有可能相交 的两线段计算交点,对不可能相交的线段 不计算交点,使算法有更好的效率

我们称平面内两条线段在横 坐标x处是可比较的,如果存在一 条通过x的垂直线,此线与两条线 段都相交。我们规定一个在x处的 "上面"关系为:在x处,线段S在 S,的上面,记为S>S2,如果在x处 可比较,且S与垂直线的交点位于 S,与垂直线的交点的上面
我们称平面内两条线段在横 坐标x处是可比较的,如果存在一 条通过x的垂直线,此线与两条线 段都相交。我们规定一个在x处的 "上面"关系为:在x处,线段S1在 S2的上面,记为S1 >x S2 ,如果在x处 可比较,且S1与垂直线的交点位于 S2与垂直线的交点的上面
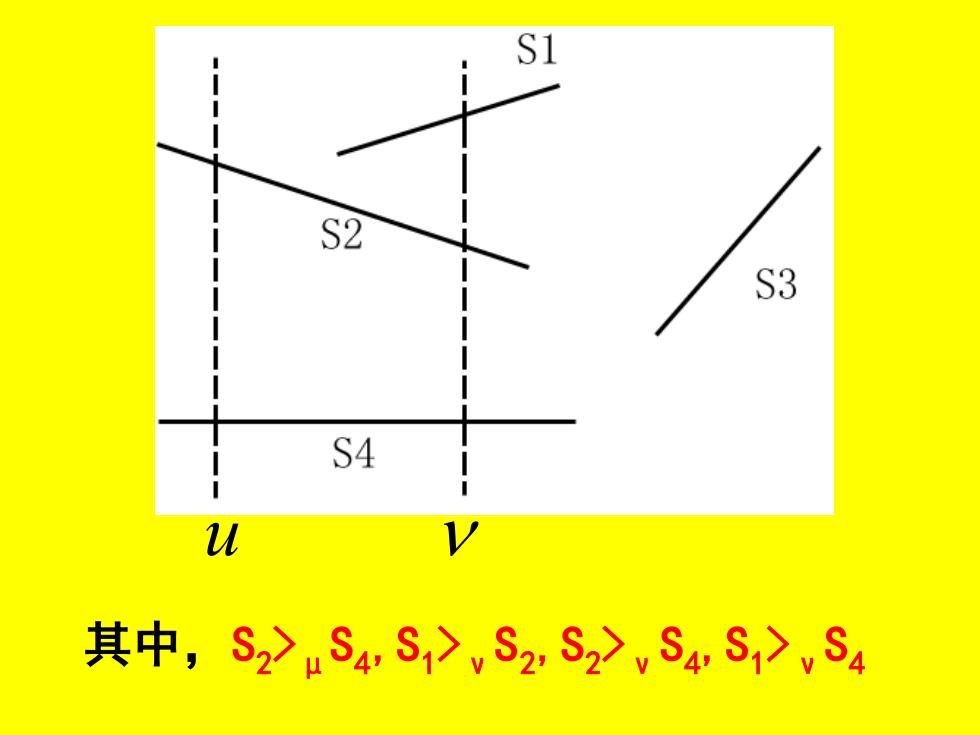
1 S2 S3 S4 u 其中,S2>uS4S1>vS2,S22,S4,S1>vS4
u 其中,S2 >μS4 ,S1 >νS2 ,S2 >νS4 ,S1 >νS4

规定的次序关系对垂直的线段不适合 两线段相交的必要条件,即若两线段相交, 则必然存在某个x,使它们在规定的次序关系 >x下是相邻的。 算法从左向右扫描,在扫描过程维持正确 的线段间上述次序关系。这种次序关系只能 有三种可能的变化方式: 1.遇见某条线段$的左端点,此时$应加入次序 关系。 2.遇见某线段$的右端点,此时$应从次序关系 中删除。 3.遇到某两条线段$和S,的交点,这时在次 序关系中S和S,交换位置
规定的次序关系对垂直的线段不适合 两线段相交的必要条件,即若两线段相交, 则必然存在某个x,使它们在规定的次序关系 >x下是相邻的。 算法从左向右扫描,在扫描过程维持正确 的线段间上述次序关系。这种次序关系只能 有三种可能的变化方式: 1.遇见某条线段S的左端点,此时S应加入次序 关系。 2.遇见某线段S的右端点,此时S应从次序关系 中删除。 3.遇到某两条线段S1和S2 的交点,这时在次 序关系中S1和S2交换位置