
·凸多边形重叠计算 两个凸多边形的重叠问题,这也就是对 两个凸多边形求相文部分的问题。 现在约定凸多边形指它的边界和内部, 凸多边形仍用顶点坐标的逆时针方向序列 确定。 设给出的两个凸多边形卯和Q的顶点序列 分别是P1,P2,,P和Q1,Q2,,Qm。为说明 简便,假设P的边界上不包含Q的项点,Q的边 界也不包含P的顶点
• 凸多边形重叠计算 两个凸多边形的重叠问题,这也就是对 两个凸多边形求相交部分的问题。 现在约定凸多边形指它的边界和内部, 凸多边形仍用顶点坐标的逆时针方向序列 确定。 设给出的两个凸多边形P和Q的顶点序列 分别是P1 ,P2 ,…,PL和Q1 ,Q2 ,…,Qm。为说明 简便,假设P的边界上不包含Q的项点,Q的边 界也不包含P的顶点

有两个问题需要解决,一个是如何有次 序地求出各边的所有交点,一个是如何排列 求出交点和原凸多边形的顶点,形成交得凸 多边形的顶点序列。 为了有次序地求出交点,可以在两个多 边形边上交替地前进,原则是在哪个多边形 的边上可能有交点就等待,在另一个多边形 的边上前进。初始从对边PP,与QQ的求交 开始,注意所有求交是线段的求交。这里规 定了PoP,Q0Qm
有两个问题需要解决,一个是如何有次 序地求出各边的所有交点,一个是如何排列 求出交点和原凸多边形的顶点,形成交得凸 多边形的顶点序列。 为了有次序地求出交点,可以在两个多 边形边上交替地前进,原则是在哪个多边形 的边上可能有交点就等待,在另一个多边形 的边上前进。初始从对边P0 P1与Q0 Q1的求交 开始,注意所有求交是线段的求交。这里规 定了P0 =PL ,Q0 =Qm
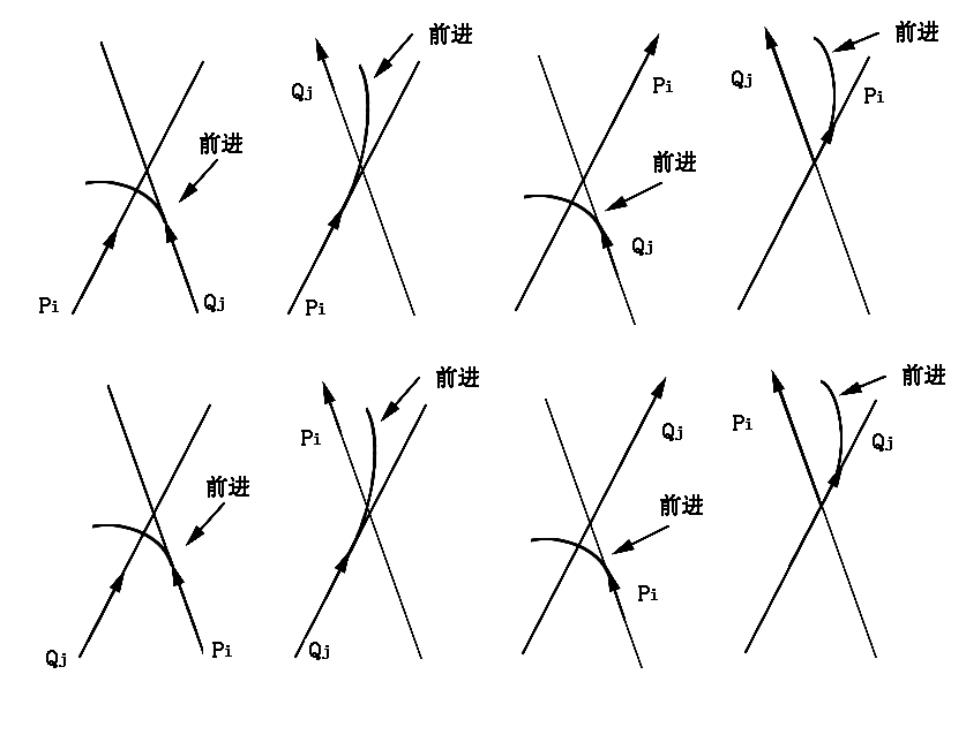
前进 前进 出 前进 Q
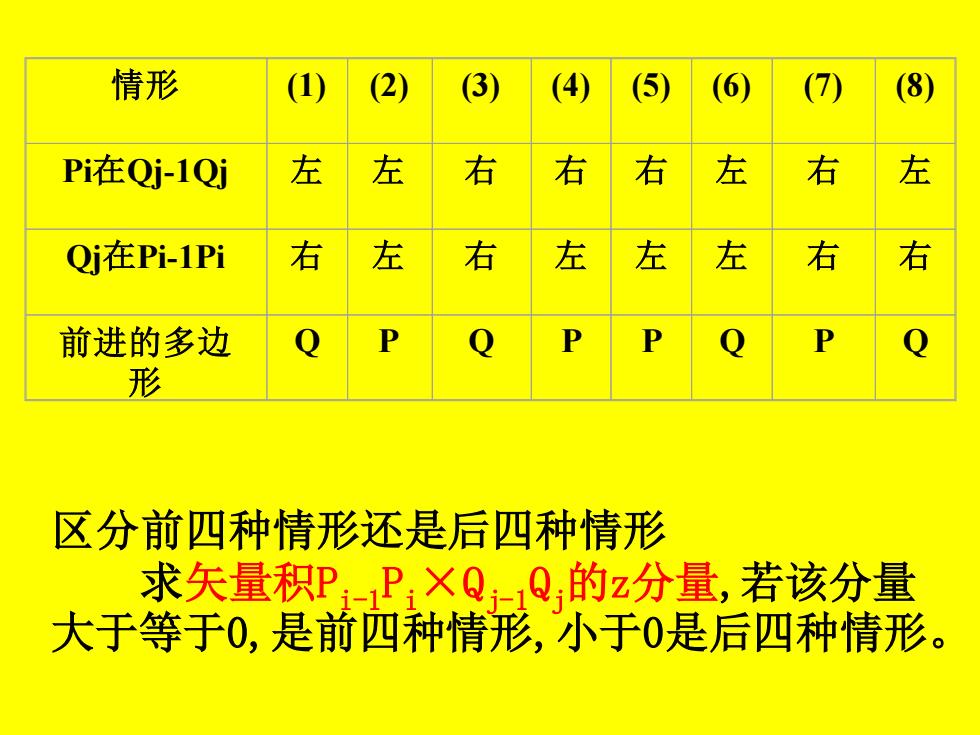
情形 (1) (2) (3) (4) (5) (6) (7) (8) P在Qj-1Qj 左 左 右 右 右 左 右 左 Qj在Pi-1Pi 右 左 右 左 左 左 右 右 前进的多边 形 区分前四种情形还是后四种情形 求矢量积P-P,×Q:Q;的z分量,若该分量 大于等于0,是前四种情形,小于0是后四种情形
情形 (1) (2) (3) (4) (5) (6) (7) (8) Pi在Qj-1Qj 左 左 右 右 右 左 右 左 Qj在Pi-1Pi 右 左 右 左 左 左 右 右 前进的多边 形 Q P Q P P Q P Q 区分前四种情形还是后四种情形 求矢量积Pi-1 Pi×Qj-1 Qj的z分量,若该分量 大于等于0,是前四种情形,小于0是后四种情形

·Advance S←PP:XQQ的z分量;分二种情况处 理,然后算法就结束; 1.若S≥0,则做 若P在Q1Q左并且Q在yP左,或者P在Q 1Q,右并且Q在pP左,则前进1,否则j前进 2.若S<0,则做 若P在Q1Q右并且Q在PP左,或者P在Q Q右并直Q在PP右,则前进1,否则j前进1; 算法中"前进1",指若i<l,则前进1是+1;若 i=L,则前进1是1。这因为多边形P是首尾相接 的。类似地"'j前进1",j<m时是j+1;j=m时是1。 总在多边形P上前进,在Q上前进
• Advance S←Pi-1Pi×Qj-1Qj的z分量;分二种情况处 理,然后算法就结束; 1. 若S≥0,则做 若Pi在Qj-1Qj左并且Qj在Pi-1Pi左,或者Pi在Qj- 1Qj右并且Qj在pi-1Pi左,则i前进1,否则j前进1; 2. 若S<0,则做 若Pi在Qj-1Qj右并且Q在Pi-lPi左,或者Pi在Qj- 1Qj右并且Qj在Pi-1Pi右,则i前进1,否则j前进1; 算法中"i前进1",指若i<l,则前进1是i+1;若 i=L,则前进1是1。这因为多边形P是首尾相接 的。类似地"j前进1",j<m时是j+1;j=m时是1。 i总在多边形P上前进,j在Q上前进