华中科技大学：《数控技术》课程教学资源（PPT课件）第4章 进给伺服驱动系统 4.5 进给系统性能分析

4.5伺服系统性能分析 4.机械传动与执行单元的数学模型 机械传动与执行单元的输入为电机的角位移0m,输出 为工作台的线位移X,其机械系统力平衡方程为： m+C,。+F。=K(2元0.-X, Fp FcFc 拉氏变换： X,6)红c,3+ K 20m(S)- mS2+CS+K F,(S) 11

11 4. 机械传动与执行单元的数学模型 机械传动与执行单元的输入为电机的角位移θm，输出 为工作台的线位移X0，其机械系统力平衡方程为：        - p + + =   D m 0 0 0 r X 2 L m X C X F K F D = FC + FCr ( ) ( ) F (S ) mS C S K 1 S mS C S K K 2 L X S D r m 2 r 0 2 + +  - + +  p = 拉氏变换： 4.5 伺服系统性能分析

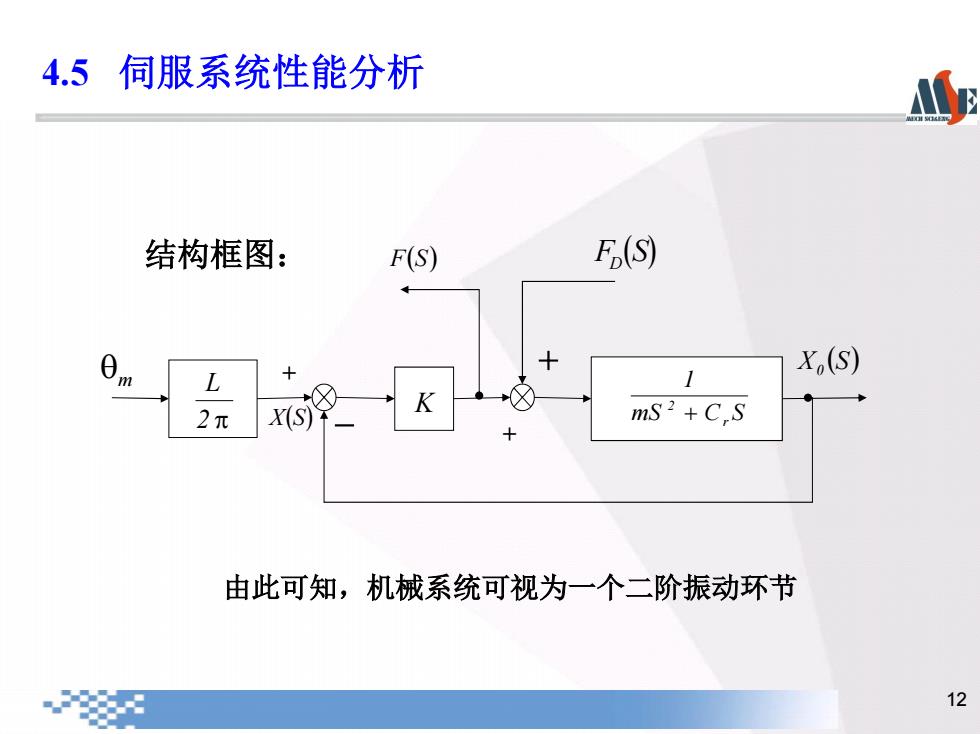
4.5伺服系统性能分析 A 结构框图： F(S) E(S) Xo(S) m L 1 2元 X(S) mS2+CS 由此可知，机械系统可视为一个二阶振动环节 12

12 结构框图： 2 p L K X (S) 0 m X(S) mS C S 1 r 2 + F (S) D － + + ＋ F(S) 由此可知，机械系统可视为一个二阶振动环节 4.5 伺服系统性能分析

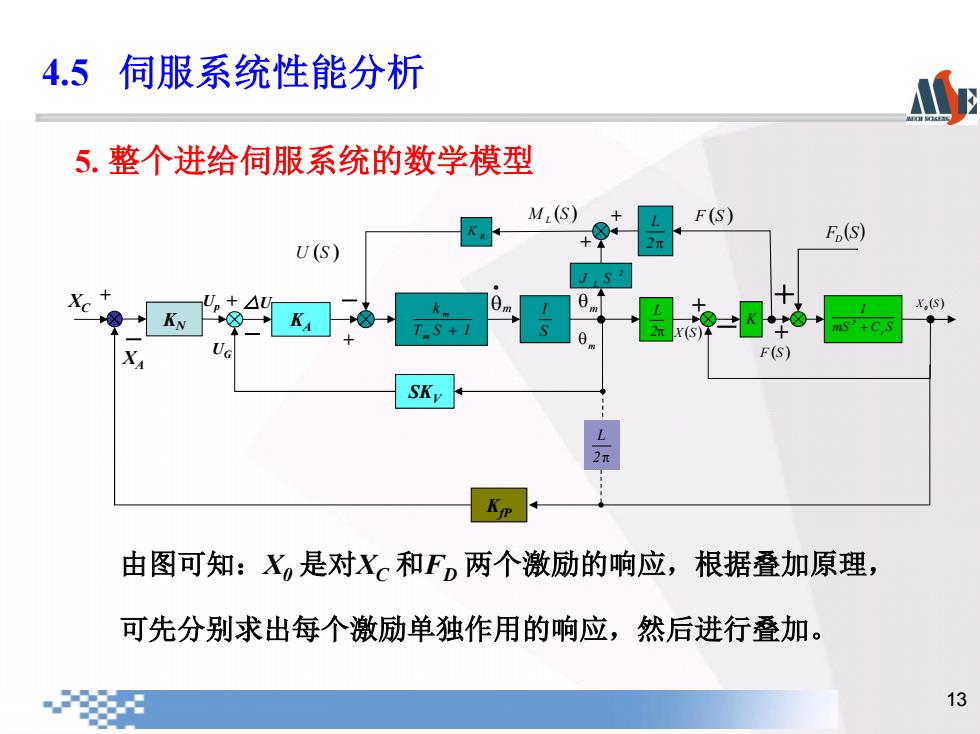
4.5伺服系统性能分析 5.整个进给伺服系统的数学模型 M(S) F(S) Fp(S) U(S) x,(s) T S+ X F(S) Kp 由图可知：X,是对X。和F,两个激励的响应，根据叠加原理， 可先分别求出每个激励单独作用的响应，然后进行叠加。 13

13 5. 整个进给伺服系统的数学模型 由图可知：X0 是对XC 和FD 两个激励的响应，根据叠加原理， 可先分别求出每个激励单独作用的响应，然后进行叠加。 KN KfP + － XA XC KA SKV + － UG m △U T S 1 k m m + S 1 2 L J S 2p L K R F (S ) U (S ) m   + － + + M (S ) L 2p L K X (S ) m 0 X (S ) mS C S 1 r 2 + F (S) D － + + ＋ F (S ) Up 2p L 4.5 伺服系统性能分析

4.5伺服系统性能分析 当FD=O时，仅有Xc激励的传递系数 闭环 G(S)= Xo h 半闭环 G(S)= X h Xc ass+bS4+cS3+d's2+e'S+h 14

14 当FD=0时，仅有XC 激励的传递系数 ( ) aS bS cS dS eS h h X X G S C + + + + + = = 5 4 3 2 闭环 0 ( ) aS bS cS d S e S h h X X G S C + + +  +  +  = = 5 4 3 2 半闭环 0 4.5 伺服系统性能分析

4.5伺服系统性能分析 口当Xc,Fo同时激励时系统的响应 闭环 xs-asx付o9-o6时 E(5) 半闭环 -x付心恩装-时 15

15  当XC , FD同时激励时系统的响应 ( ) ( ) ( ) ( ) ( )       +         - + + = - 1 1 0 2 G S K K K K K mS C S K F S X S G S X S N A P R r D 闭环 C ( ) ( ) ( ) ( ) ( )        +         - + + =  - 1 1 0 2 G S K K K K K mS C S K F S X S G S X S N A P R r D 半闭环 C 4.5 伺服系统性能分析