
4.5伺服系统性能分析 1.位置控制单元的数学模型 位置控制单元是以Xc为输入以Up为输出的一个控 制环节,位置调节器一般采用比例调节,放大系数 为Kv,则有: =KxAD=Kx(Xc-X)=Kv(Xc-KpXo) 取拉氏变换得: US)=KNXc(S)-KPX(S月 结构框图: KN Xo Kr 6
6 1. 位置控制单元的数学模型 位置控制单元是以XC为输入以 UP为输出的一个控 制环节,位置调节器一般采用比例调节,放大系数 为KN,则有: 取拉氏变换得: 结构框图: ( ) ( ) U P = KN DD = KN X C - X A = KN X C - K fP X 0 ( ) X (S ) K X (S ) U P S = K N C - fP 0 KN KfP + - X X0 A XC Up 4.5 伺服系统性能分析
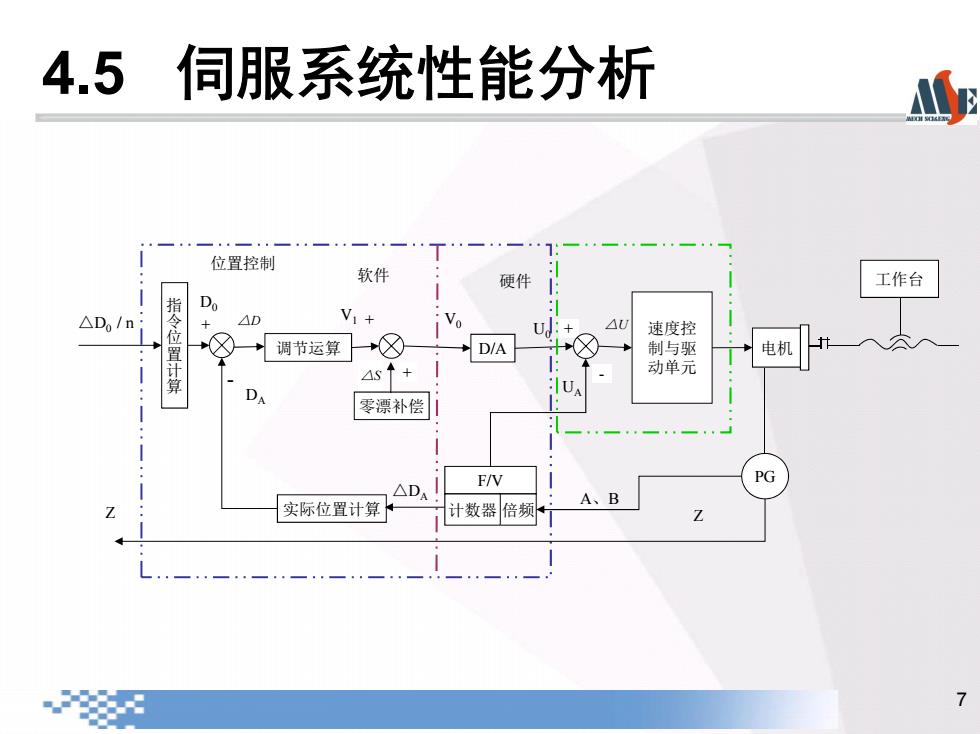
4.5 伺服系统性能分析 位置控制 软件 硬件 工作台 △Do/n 指令位 D AD V1+ U:+ △U 速度控 调节运算一+公 D/A (X) 制与驱 电机 4s↑+ 动单元 UA 零漂补偿山 F/V △D 实际位置计算 A、B 计数器倍频 7
7 + 调节运算 零漂补偿 硬件 速度控 制与驱 动单元 D/A 软件 位置控制 Z A、B D0 - + + - F/V 计数器 倍频 工作台 PG 电机 + DA V1 △S V0 U0 UA △D △U 实际位置计算 △DA 指令位置计算 △D0 / n Z 4.5 伺服系统性能分析

4.5伺服系统性能分析 2.速度控制单元的数学模型 速度控制单元是以指令电压Up为输入,电机的驱动电压U为输 出的控制环节,速度调节器通常采用P调节,驱动放大是比例环 节,若忽略非线性和滞后特性的影响,可视它们为比例环节,则 传递函数为K4,速度反馈环节的传递函数为Kv,则有: U=K,Up-UG)=KUp-K,0】 取拉氏变换 U=K4[Up(S)-KyS0m(s】 结构框图: Up △U KA SKv 8
8 2. 速度控制单元的数学模型 速度控制单元是以指令电压UP 为输入,电机的驱动电压U为输 出的控制环节,速度调节器通常采用PI调节,驱动放大是比例环 节,若忽略非线性和滞后特性的影响,可视它们为比例环节,则 传递函数为KA ,速度反馈环节的传递函数为KV ,则有: 取拉氏变换得: 结构框图: ( ) = - = - U K A U P U G K A U P KV m U K U (S ) K S (s) = A P - V m KA SKV + - UG UP U m △U 4.5 伺服系统性能分析

4.5伺服系统性能分析 3.直流伺服电机的数学模型(交流电机模型类似) 直流伺服电机是以驱动电压U为输入,电机的角位移日m为输 出的变换环节,其数字模型是根据电机电枢电势平和电机转 矩衡方程导出的。 U= T 16m+krMr 0m十 km km 式中: Tm-RKeKT 电机的机械时间常数 Km-1/Ke 电机的增益系数 Kg-Ra/KT ML=J:0m+L 2元 M,(S)=J,0(S)s2+2FS) 2元 9
9 3. 直流伺服电机的数学模型(交流电机模型类似) 直流伺服电机是以驱动电压U为输入,电机的角位移m为输 出的变换环节,其数字模型是根据电机电枢电势平和电机转 矩衡方程导出的。 m R L m m m m k M k 1 k T U = + + 式中: Tm=RaJ a/ KeKT 电机的机械时间常数 Km=1 / Ke 电机的增益系数 KR=Ra / KT p = + 2 FL M L J L m ( ) ( ) F (S ) 2 L M S J S S 2 L L m p = + 4.5 伺服系统性能分析

4.5伺服系统性能分析 拉氏变换得: TS+1 S M L TS+1 S 7号r9).s0.6)会r明 结构框图: Mi(S) L F(S) 2π U(S) TS+1 S 而且经适当的简化后,直流伺服电机可视为一个 惯性环节和一个积分环节串联而成。 10
10 拉氏变换得: ( ) ( ) ( ) ( ) ( ) p - + + = + - + = F S 2 L U S K J S S S 1 T S 1 K M S 1 T S 1 K K U S S 1 T S 1 K S m 2 R L m m L m m R m m m 结构框图: T S 1 k m m + S 1 2 J L S 2 p L K R F (S ) m U (S ) m + - + + M (S ) L 而且经适当的简化后,直流伺服电机可视为一个 惯性环节和一个积分环节串联而成。 4.5 伺服系统性能分析