结构力学一第十二章结构的动力计算 海南大学土木建筑工程学院 例题12.1:图示为多跨静定梁。支座B为弹性支承,弹簧的刚度 系数为k;F端装有阻尼器,阻尼系数为c;杆DF和AC为无限 刚性并不计质量,杆DF上有两个各为m的集中质量。试建立振 动方程。 (a) 解:设振动中取AB杆,A 端转角0为参考坐标 a a2 弹性力kaa惯性力mad b 阻尼力2caa 方向都与运动方向相反。 (C、DF隔离体∑ME=0 Fya-mada-2cada=0 (c) Fy mad +2cad (d)、DF隔离体∑M4=0 (d) 2Fxa+k aaa-F(t)a=0 整理得振动方程:md+2ca+。k1, F(+) 12 2 2a 多跨静定梁
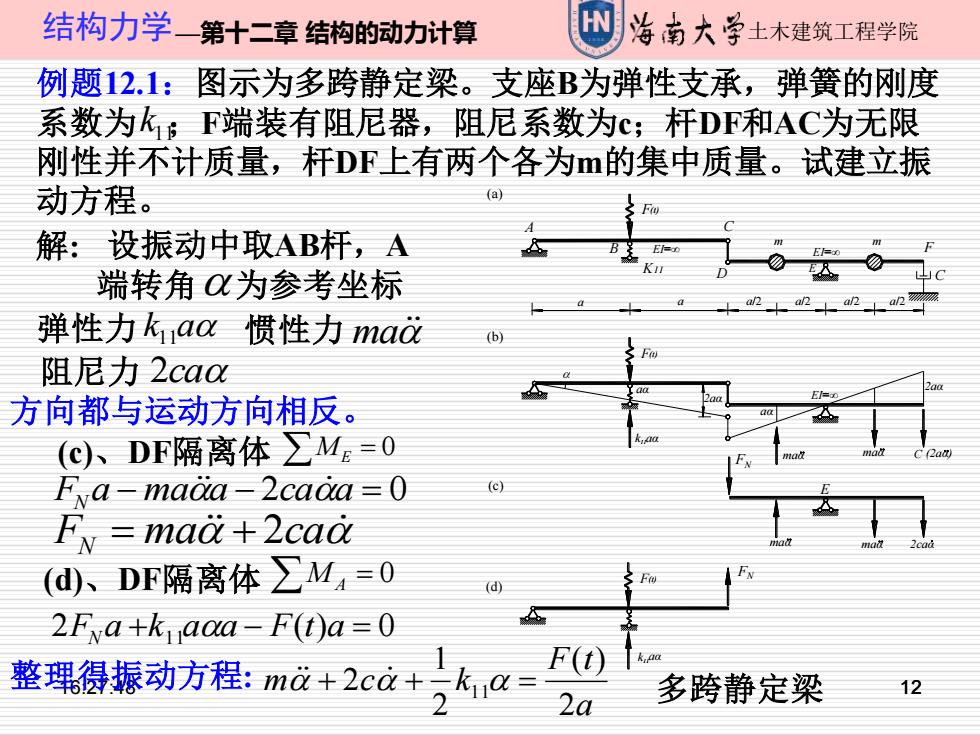
16:27:48 12 结构力学—第十二章 结构的动力计算 土木建筑工程学院 12 例题12.1:图示为多跨静定梁。支座B为弹性支承,弹簧的刚度 系数为 ;F端装有阻尼器,阻尼系数为c;杆DF和AC为无限 刚性并不计质量,杆DF上有两个各为m的集中质量。试建立振 动方程。 11 k F(t) (d) (c) E C F(t) EI=∞ (b) (a) a a a m m EI=∞ C F D A C K11 B EI=∞ F(t) E aα 2aα aα 2aα (2aα) k11aα maα maα maα maα 2caα k11aα FN FN /2 a/2 a/2 a/2 多跨静定梁 解: 设振动中取AB杆,A 端转角 为参考坐标 弹性力 惯性力 阻尼力 k11a ma 2ca 方向都与运动方向相反。 (c)、DF隔离体 ME = 0 FN a − ma a − 2ca a = 0 F ma ca N = + 2 (d)、DF隔离体 M A = 0 2FN a +k11aa − F(t)a = 0 a F t m c k 2 ( ) 2 1 整理得振动方程: + 2 + 11 =

结构力学一第十二章结构的动力计算 洛南大学土木建筑工程学院 例题12.2:图示结构,不计阻尼,试建立振动方程。 m 解:图示刚架质点作水平振动, F(t) (a) 现以柔度法建立振动方程,步骤如下: E=常数 作出M,图和M。图,求出柔度系数为 2a 2a 5a3 3E1 El 质点m沿水平方向振动时任 b 时刻的位移为: y=O(-m)+δEF(t M图 将O、OF代入上式,即得 5a y= -m))+ F(t) (c) 3EI El 整理得振动方程:少+ 3E1 3 5ma F() a 16:27:48 5m M图 13
16:27:48 13 结构力学—第十二章 结构的动力计算 土木建筑工程学院 13 例题12.2: 图示结构,不计阻尼,试建立振动方程。 m 2a a 2a F(t) EI=常数 a a a F=1 1 (a) (b) (c) M1图 MF图 解: 图示刚架质点m作水平振动, 现以柔度法建立振动方程,步骤如下: 作出 M1 图和 M F 图,求出柔度系数为 EI a 3 5 3 11 = EI a F 2 1 = 质点m沿水平方向振动时任 一时刻的位移为: ( ) ( ) 11 1 y my F t = − + F 将 11、 1F 代入上式,即得 ( ) ( ) 3 5 3 3 F t EI a my EI a y = − + ( ) 5 3 5 3 3 F t m y ma EI 整理得振动方程:y + =

结构力学一第十二章结构的动力计算 W 海南大学士木建筑工程学院 12.3单自由度体系的自由振动 在没有动力荷载(即F)=0)作用时所发生的振动称为自由振动 体系的自由振动是由初位移或初速度激发产生的。自由振动的 分析将能揭示体系本身的特性。自由振动又分为无阻尼和有阻 尼两种情况,现分别阐述如下。 123.1无阻尼自由振动 根据公式砂+少+ky=F())并令Ft)=0,F.)=0 即无阻尼自由振动方程为: 吵+k1y=0→+02y=0(0 y(1)=C sin@t+C2 cos@t 00之G8 y(0)=y0→C2=y0 16:27:48 14
16:27:48 14 结构力学—第十二章 结构的动力计算 土木建筑工程学院 14 在没有动力荷载(即 F(t) =0)作用时所发生的振动称为自由振动 体系的自由振动是由初位移或初速度激发产生的。自由振动的 分析将能揭示体系本身的特性。自由振动又分为无阻尼和有阻 尼两种情况,现分别阐述如下。 12.3.1无阻尼自由振动 根据公式 ( ) 11 m y + cy + k y = F t 并令 F(t) = 0,Fc (t) = 0 即无阻尼自由振动方程为: m y + k11y = 0 0 2 y+w y = . ( ) m k w = ( ) sin cos 1 2 y t =C wt+C wt 12.3 单自由度体系的自由振动 (0) 0 0 1 w = = v y v C . (0) 0 2 0 y = y C = y

结构力学一第十二章结构的动力计算 海南大学士木建筑工程学院 单自由度体系无阻尼 ( 自由振动的解 vo/o (t)yocosin 0 -vo/@ T a y(t)=asin(@t+a) 16:27:48 15
16:27:48 15 结构力学—第十二章 结构的动力计算 土木建筑工程学院 15 y(t )=asin(wt+) ( ) cos sin 0 0 w w = w + t v y t y t y(t) t y0 -y0 y(t ) t v0 /ω -v0 /ω T t a -a T α/ω T 单自由度体系无阻尼 自由振动的解

结构力学一第十二章结构的动力计算 洛南大学土木建筑工程学院 v(t)=asin(@t+a)=asinacosot+acosasin@t (t)=yocosin @i 2 振幅:Q三1 yo =asina Yo=acos( 0 无阻尼自由振动是简谐振动 初始相位角:C=g 100 vo 结构的自振周期 )=usi2)asin() 周期函数的条件:yt+T)=yt) (t)=asin(or+o是周期函数,且周期是: T_2a 0 0 频率72元 圆频率:0 2π=2∫ T 秒钟内的振动次数 2π秒内的振动次数。 16
16:27:48 16 结构力学—第十二章 结构的动力计算 土木建筑工程学院 16 y(t )=asin(wt+) ( ) cos sin 0 0 w w = w + t v y t y t 0 1 0 v y tg w − = 2 2 2 0 0 , v a y w 0 = + acos v w = 0 y =asin =asin coswt+acossinwt 振幅: 初始相位角: 结构的自振周期 y(t)=asin(wt+) ) 2 ( w p ) )= y t+ 2 sin( ( w p =asin(wt+ +2p )=a w t+ + 周期函数的条件: y(t+T )=y(t ) y(t)=asin(wt+) 是周期函数,且周期是: w 2p T = 频率: p w 2 1 = = T f 每秒钟内的振动次数. 圆频率: f T p p w 2 2 = = 2π秒内的振动次数. 无阻尼自由振动是简谐振动