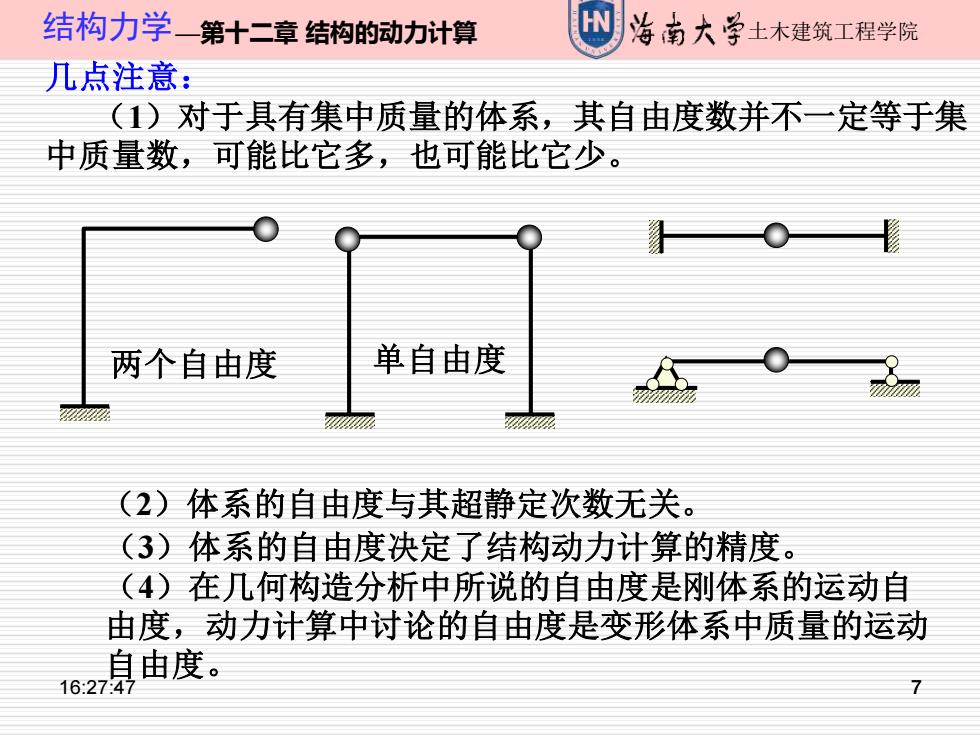
结构力学一第十二章结构的动力计算 海南大学土木建筑工程学院 几点注意: (1)对于具有集中质量的体系,其自由度数并不一定等于集 中质量数,可能比它多,也可能比它少。 两个自由度 单自由度 Z E (2)体系的自由度与其超静定次数无关。 (3)体系的自由度决定了结构动力计算的精度。 (4)在几何构造分析中所说的自由度是刚体系的运动自 由度,动力计算中讨论的自由度是变形体系中质量的运动 自由度。 16:274
16:27:47 7 结构力学—第十二章 结构的动力计算 土木建筑工程学院 7 几点注意: (1)对于具有集中质量的体系,其自由度数并不一定等于集 中质量数,可能比它多,也可能比它少。 (2)体系的自由度与其超静定次数无关。 (3)体系的自由度决定了结构动力计算的精度。 (4)在几何构造分析中所说的自由度是刚体系的运动自 由度,动力计算中讨论的自由度是变形体系中质量的运动 自由度。 两个自由度 单自由度

结构力学一第十二章结构的动力计算 海南大学士木建筑工程学院 12.2单自由度体系的振动方程 单自由度体系动 ①具有实际应用价值,或进行初步的估算。 力分析的重要性 ②多自由度体系动力分析的基础。 振动微分方程的建立的依据原理:达朗伯原理。 有刚度法与柔度法两种基本方法。 12.2.1刚度法从力系平衡角度建立的自由振动微分方程 (a) (b) m yo FO F 振动模型图 16:27:47 8
16:27:47 8 结构力学—第十二章 结构的动力计算 土木建筑工程学院 8 12.2单自由度体系的振动方程 单自由度体系动 力分析的重要性 ①具有实际应用价值,或进行初步的估算。 ②多自由度体系动力分析的基础。 振动微分方程的建立的依据原理:达朗伯原理。 有刚度法与柔度法两种基本方法。 12.2.1刚度法 从力系平衡角度建立的自由振动微分方程 c (a) (b) FS FC FI F(t) m F(t) y(t) 振动模型图

结构力学一第十二章结构的动力计算 治南大学土木建筑工程学院 质点隔离体上受到以下四种力作用: (1D动力荷载: (2)阻尼力:F) 在体系振动过程中,实际上都会遇到不同程度的阻力作用。 这种阻力通常称为阻尼力。本章只介绍粘滞阻尼力,阻尼力 的大小和质量运动的速度成正比,它的数学表达式为: Fc(t)=-ci (3)弹性力E) 弹性力是在振动过程中,由于杆件的弹性变形所产生的恢复力。 它的大小与质量的位移成正比,但方向相反,可表示为: E.0=-ky) (4)惯性力E) 它的大小等于质量与其位移加速度的乘积,而方向与加速方 向相反,可表示为:F=-) 16:27:48 9
16:27:48 9 结构力学—第十二章 结构的动力计算 土木建筑工程学院 9 质点隔离体上受到以下四种力作用: F(t) F (t) C (1)动力荷载 : (2)阻尼力 : 在体系振动过程中,实际上都会遇到不同程度的阻力作用。 这种阻力通常称为阻尼力。本章只介绍粘滞阻尼力,阻尼力 的大小和质量运动的速度成正比,它的数学表达式为: F (t) C =- cy F (t) s ( ) ( ) 11 F t k y t s = − .(3)弹性力 弹性力是在振动过程中,由于杆件的弹性变形所产生的恢复力。 它的大小与质量的位移成正比,但方向相反,可表示为: F (t) (4)惯性力 I 它的大小等于质量与其位移加速度的乘积,而方向与加速方 向相反,可表示为: F (t) my(t) I = −

结构力学一第十二章结构的动力计算 洛南大学士木建筑工程学院 根据达朗贝尔原理,可列出质点隔 离体的平衡方程为 E++E+F()=0 将:F(d)=-c E.d)-k0 质点隔离体 E(t)=-mi(t) 代入上式得: m+C少+ky=Ft) 上式是根据平衡条件建立的单自由度体系振动 方程。它是一个二阶线性常系数微分方程。这 种推导方法涉及体系的刚度系数,所以又称为 刚度法。 16:27:48 10
16:27:48 10 结构力学—第十二章 结构的动力计算 土木建筑工程学院 10 c (a) (b) FS FC FI F(t) m F(t) y(t) 质点隔离体 根据达朗贝尔原理,可列出质点隔 离体的平衡方程为 FI + Fc + FS + F(t) = 0 ( ) ( ) 11 F t k y t s = − F (t) my(t) I = − F (t) cy C 将: = − 代入上式得: ( ) 11 m y + cy + k y = F t 上式是根据平衡条件建立的单自由度体系振动 方程。它是一个二阶线性常系数微分方程。这 种推导方法涉及体系的刚度系数,所以又称为 刚度法

结构力学一第十二章结构的动力计算 海南大学士木建筑工程学院 12.2.2柔度法 振动方程也可以根据位移协调来推导。质点位移,可以视为 由于动力荷载F(t) 惯性力E@ 阻尼力F(t 共同作用下产生的。根据叠加原理,位移)可表示为 y(t)=δE(t)+δE(t)+δF(t) δ表示在质量的运动方向上施加单位力所产生的质量 沿运动方向的位移,称为柔度系数。将动力荷载、惯性力 与阻尼力的表达式代入即得: 上式是根据位移协调建立的 振动方程。这种推导方法涉 及体系的柔度系数,所以又 上述原理和方法也可用于 称为柔度法。 F6E()三力不全作用于质点上的情况。 11
16:27:48 11 结构力学—第十二章 结构的动力计算 土木建筑工程学院 11 12.2.2 柔度法 振动方程也可以根据位移协调来推导。质点位移,可以视为 由于动力荷载 F(t) F(t) 惯性力 阻尼力 F (t) I F (t) C 共同作用下产生的。根据叠加原理,位移 y(t) 可表示为 ( ) ( ) ( ) ( ) 11 11 11 y t F t F t F t = I + C + 11 表示在质量的运动方向上施加单位力所产生的质量 沿运动方向的位移,称为柔度系数。将动力荷载、惯性力 与阻尼力的表达式代入即得: ( ) 1 11 my + cy + y = F t 上式是根据位移协调建立的 振动方程。这种推导方法涉 及体系的柔度系数,所以又 上述原理和方法也可用于 称为柔度法。 F(t)、FI (t)、 F (t) C 三力不全作用于质点上的情况