
结构力学一第三章静定梁和静定刚架 W 海南大学土木建筑工程学院 第三章静定梁和静定刚架 3.1单跨静定梁 3.1.1用截面法计算指定截面内力 利用截面从结构中截取隔离体,根据隔离体平衡 方程求解截面内力的方法,称为截面法。下面以一个 例子重温这一方法。 例3-1试求图示简支梁截面B的弯矩MB、截面C 的弯矩Mc和截面D的剪力Fa 5kN/m 20kN 2m 2m 2m 2m
2 结构力学—第三章 静定梁和静定刚架 土木建筑工程学院 3.1 单跨静定梁 3.1.1 用截面法计算指定截面内力 利用截面从结构中截取隔离体,根据隔离体平衡 方程求解截面内力的方法,称为截面法。下面以一个 例子重温这一方法。 例3-1 试求图示简支梁截面B的弯矩MB、截面C 的弯矩MC和截面D的剪力FQD。 第三章 静定梁和静定刚架 A D B C E 2m 2m 2m 2m 5kN/m 20kN 5kN/m 20kN E A D B C FAy FAx FEy

结构力学一第三章静定梁和静定刚架 W 洛南大学士木建筑工程学院 解:(1)首先求出支座反力 5kN/m 20kN B 将该简支梁所有支座去除,代以相应支反 力,绘出受力图,如上图所示。对A点处取力矩 平衡方程∑M,=0,可得 2X5x4+20x6-5,×8=0 解得FEy=20kN(↑)。 3
3 结构力学—第三章 静定梁和静定刚架 土木建筑工程学院 1 2 5 4 20 6 8 0 2 + − = FEy 解:(1)首先求出支座反力 A D B C E 2m 2m 2m 2m 5kN/m 20kN 5kN/m 20kN E A D B C FAy FAx FEy 0 MA = 将该简支梁所有支座去除,代以相应支反 力,绘出受力图,如上图所示。对A点处取力矩 平衡方程 ,可得 解得FEy = 20kN(↑)
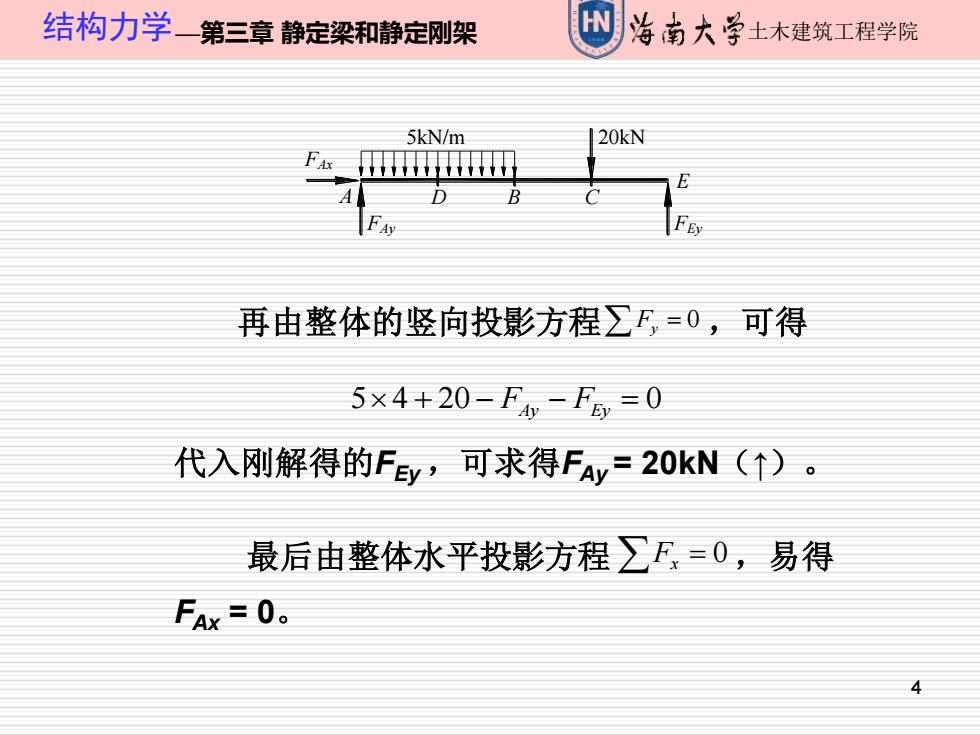
结构力学一第三章静定梁和静定刚架 治南大学土木建筑工程学院 5kN/m 20kN 再由整体的竖向投影方程E,=0,可得 5×4+20-Fy-1=0 代入刚解得的FEy,可求得FAy=20kN(↑)。 最后由整体水平投影方程∑F=0,易得 FAx=0
4 结构力学—第三章 静定梁和静定刚架 土木建筑工程学院 代入刚解得的FEy ,可求得FAy = 20kN(↑)。 再由整体的竖向投影方程 F y = 0 ,可得 5 4 20 0 + − − = F F Ay Ey A D B C E 2m 2m 2m 2m 5kN/m 20kN 5kN/m 20kN E A D B C FAy FAx FEy 最后由整体水平投影方程 ,易得 FAx = 0。 Fx = 0

结构力学一第三章静定梁和静定刚架 洛南大学士木建筑工程学院 (2)用截面法求指定截面的内力 ①求控制截面B的弯矩 截断B截面,取截面右 20kN 边部分梁段B为隔离体,绘F 出受力图,如右图所示。除 E 外荷载20kN和支反力FEy三 FEy =20kN 20kN外,还有B截面的三个 内力,即轴力FNB、剪力FaB 和弯矩MB° 因只需求弯矩MB,所以对B点列力矩平衡方 程,这样可避免FNB和FaB这两个未知力出现在 平衡方程中。即由∑M,=0,得 5
5 结构力学—第三章 静定梁和静定刚架 土木建筑工程学院 (2)用截面法求指定截面的内力 ① 求控制截面B的弯矩 截断B截面,取截面右 边部分梁段BE为隔离体,绘 出受力图,如右图所示。除 外荷载20kN和支反力FEy = 20 kN外,还有B截面的三个 内力,即轴力FNB、剪力FQB 和弯矩MB。 0 MB = 因只需求弯矩MB,所以对B点列力矩平衡方 程,这样可避免FNB和FQB这两个未知力出现在 平衡方程中。即由 ,得 20kN B C FEy E FQB FNB MB =20kN

结构力学一第三章静定梁和静定刚架 治南大学土木建筑工程学院 MB+20×2-F×4=0 解得Mg=40kNm,下侧受拉。 ②求截面C的弯矩 截断C截面,取截面右 Mc 20kN 边部分梁段CE为隔离体,绘 E 出受力图,如右图所示。与 FEy=20kN 求MB类似,由∑M=0,得 M-fF×2=0 解得Mc=40kNm,下侧受拉。 6
6 结构力学—第三章 静定梁和静定刚架 土木建筑工程学院 解得MB = 40kN·m,下侧受拉。 ②求截面C的弯矩 0 MC = 截断C截面,取截面右 边部分梁段CE为隔离体,绘 出受力图, 如右图所示。与 求MB类似,由 ,得 C 20kN FEy =20kN E MC FNC FQC 2 0 M F C Ey − = 解得MC = 40kN·m,下侧受拉。 20 2 4 0 M F B Ey + − =