
结构力学一第十二章结构的动力计算 海南大学士木建筑工程学院 自振周期计算公式的几种形式: T=2π =2πm6=2 m =2π st 圆频率计算 8 公式的几种形式: V m √mδ Vwδ st 些重要性质: (1)自振周期与且只与结构的质量和结构的刚度有关, 与外界的干扰因素无关。干扰力只影响振幅。 W是质 (2)自振周期与质量的平方根成正比,质量 越大(频率越小);自振周期与刚度的平方根成 点的重力 越大,周期越小(频率越大)。 (3)两个外形相似的结构,如果周期相差悬殊,则动力 性能相差很大。反之,两个外形看来并不相同的结构,如果 其自振周期相近,则在动荷载作用下的动力性能基本一致
16:27:48 17 结构力学—第十二章 结构的动力计算 土木建筑工程学院 17 自振周期计算公式的几种形式: g st D =2p g W = =2p m 2p k m T = =2p w 2p 圆频率计算 公式的几种形式: st g D = W g = m k w = m = 1 其中δ——是沿质点振动方向的结构柔度系数,它表示在质 点上沿振动方向加单位荷载使质点沿振动方向所产生的位移。 k——使质点沿振动方向发生单位位移时,须在质点上沿振动 方向施加的力。 Δst=Wδ——在质点上沿振动方向施加数值为W的荷载时质 点沿振动方向所产生的位移。 计算时可根据体系的具体情况,视δ、 k、 Δst 三则中哪一 个最便于计算来选用。 一些重要性质: (1)自振周期与 且只与结构的质量和结构的刚度有关, 与外界的干扰因素无关。干扰力只影响振幅 a。 (2)自振周期与质量的平方根成正比,质量越大,周期 越大(频率越小);自振周期与刚度的平方根成反比,刚度 越大,周期越小(频率越大)。 (3)两个外形相似的结构,如果周期相差悬殊,则动力 性能相差很大。反之,两个外形看来并不相同的结构,如果 其自振周期相近,则在动荷载作用下的动力性能基本一致。 W是质 点的重力
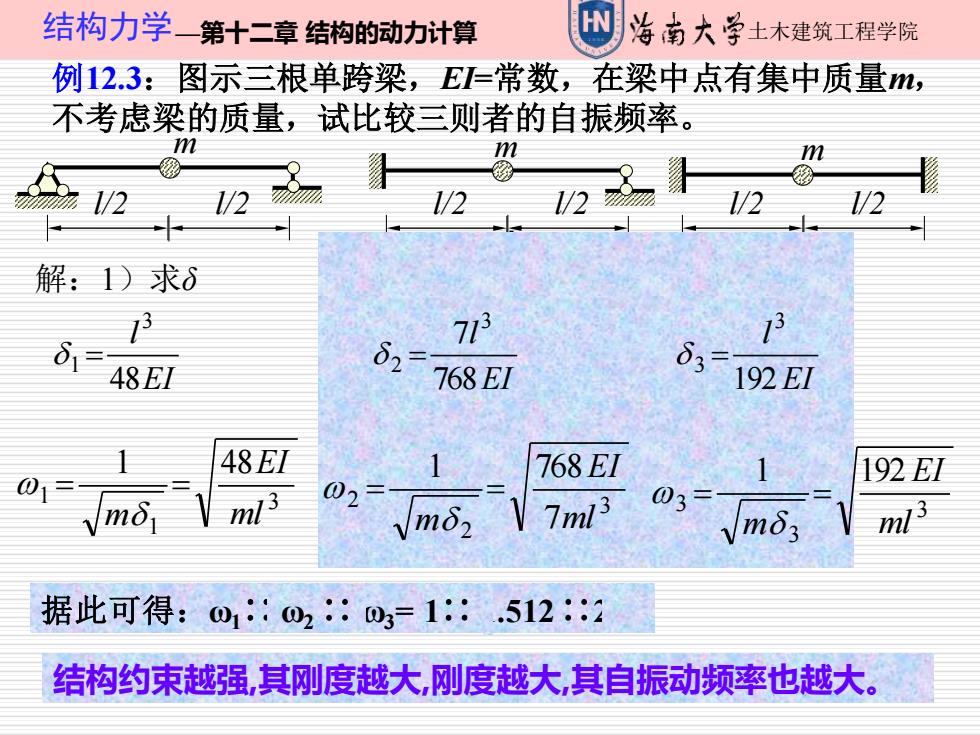
结构力学一第十二章结构的动力计算 四海南大学土木建筑工程学院 例12.3:图示三根单跨梁,E=常数,在梁中点有集中质量m, 不考虑梁的质量,试比较三则者的自振频率。 m m 12 /2 1/2 12 1/2 1/2 解:1)求δ 713 1 48EI 62 768EI 63 192EI 48EI 768EI 192E1 01 ml3 03 7ml3 03 √mδ2 Vmδ3 ml 据此可得:01:02:0=1:.5122 结构约束越强,其刚度越大刚度越大,其自振动频率也越大
16:27:49 18 结构力学—第十二章 结构的动力计算 土木建筑工程学院 18 例12.3:图示三根单跨梁,EI=常数,在梁中点有集中质量m, 不考虑梁的质量,试比较三则者的自振频率。 l/2 l/2 l/2 l/2 l/2 l/2 m m m 解:1)求δ EI l 48 3 1 = 3l / P=1 16 5l /32 l / P=1 2 EI l l l l l EI l 768 7 ) 32 5 16 2 3 2 (2 6 1 3 2 1 = − = EI l 768 7 3 2 = EI l 192 3 3 = 3 1 1 1 48 ml EI m = = w 3 2 2 7 1 768 ml EI m = = w 3 3 3 1 192 ml EI m = = w 据此可得:ω1∷ ω2 ∷ ω3= 1∷ 1.512∷2 结构约束越强,其刚度越大,刚度越大,其自振动频率也越大
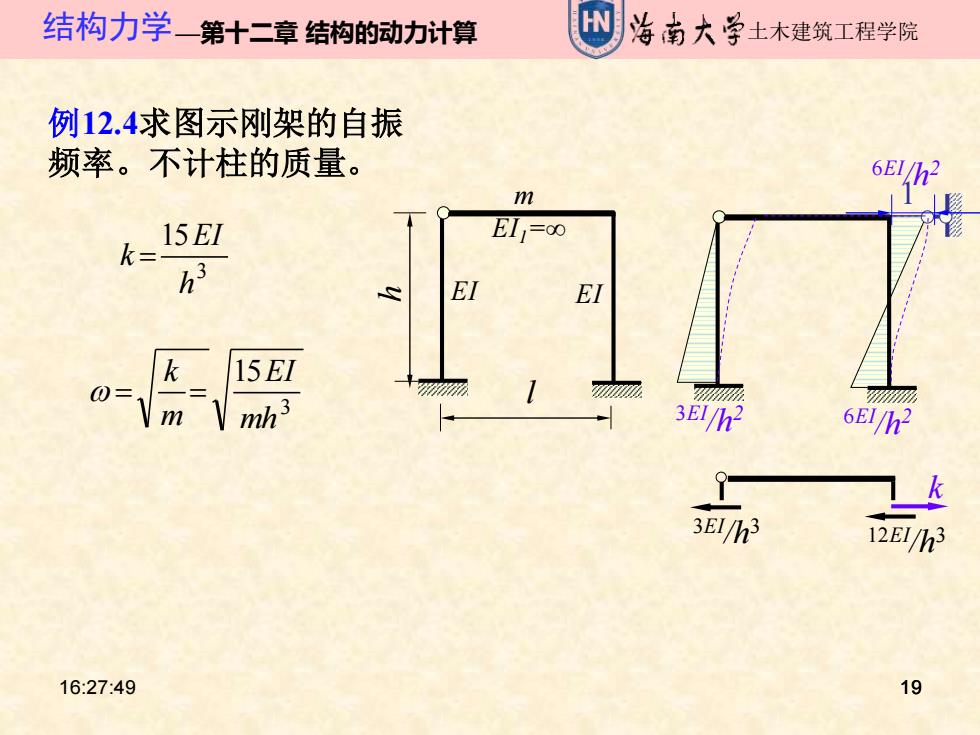
结构力学一第十二章结构的动力计算 海南大学土木建筑工程学院 例12.4求图示刚架的自振 频率。不计柱的质量。 m k=15E E11=00 h EI k 15EI 0二1 m mh3 3E/2 6E/2 k 3EI/h3 12E/h3 16:27:49 19
16:27:49 19 结构力学—第十二章 结构的动力计算 土木建筑工程学院 19 例12.4求图示刚架的自振 频率。不计柱的质量。 EI EI EI1=∞ m l h 1 3EI/h2 6EI/h2 6EI/h2 k 12EI/h3 3EI/h3 3 15 h EI k = 3 15 mh EI m k w = =
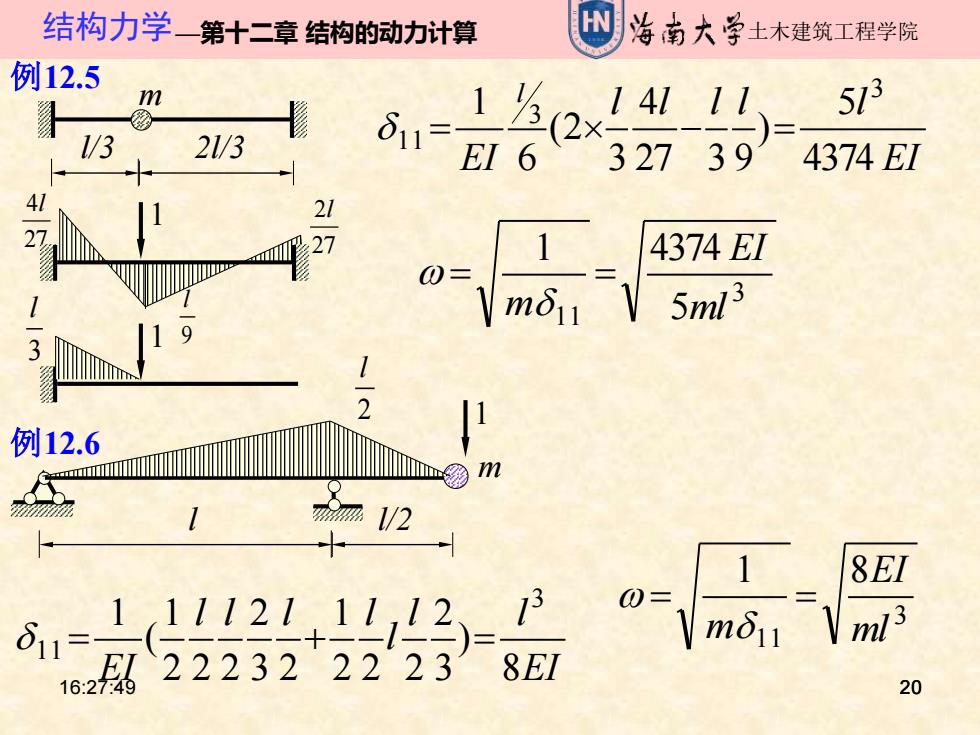
结构力学一第十二章结构的动力计算 W 治南大学土木建筑工程学院 例12.5 m /3 2/3 152x1 573 EI632739 4374EI 41 21 27 4374EI 0= 5ml3 2 例12.6 . m多m ml1/2 1 8EI 111121.11,12 13 O-mt ml3 222322223 8EI 20
16:27:49 20 结构力学—第十二章 结构的动力计算 土木建筑工程学院 20 27 4l 27 2l 9 l 1 1 3 l EI l l l l l EI l 4374 5 ) 27 3 9 4 3 (2 6 1 3 3 1 1= − = 3 11 5 1 4374 ml EI m = = w l/3 2l/3 m 例12.5 例12.6 l l/2 m 2 1 l EI l l l l l l l EI 8 ) 3 2 2 2 2 1 3 2 2 2 2 2 1 ( 1 3 1 1= + = 3 11 1 8 ml EI m = = w
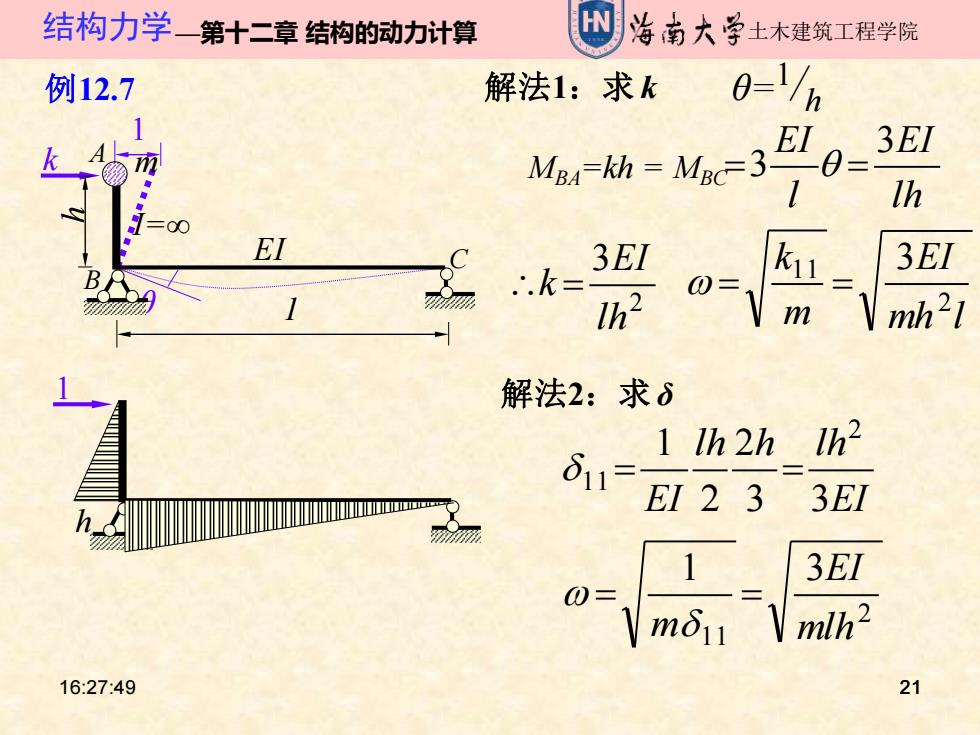
结构力学一第十二章结构的动力计算 海南大学土木建筑工程学院 例12.7 解法1:求k Mh=Mc=3以 3EI Ih 3EI 3EI 1h2 0= m mh21 解法2:求6 1 Ih2h Th2 δ11 I- EI 2 3 3EI 猛 1 3EI 0= m61 mlh2 16:27:49 21
16:27:49 21 结构力学—第十二章 结构的动力计算 土木建筑工程学院 21 1 θ 例12.7 解法1:求 k θ=1 /h MBA=kh = MBC k 1 h m I=∞ EI B A C lh EI l EI 3 =3 = mh l EI m k 2 1 1 3 w = = 2 3 lh EI k = 1 h 解法2:求 δ EI lh h lh EI 3 3 2 2 1 2 11= = 2 11 1 3 mlh EI m = = w