
结构力学一第十二章结构的动力计算 四洛南大学土木建筑工程学院 第十二章、结构的动力计算 本章导读 ●本章教学的基本要求:掌握结构体系动力自由度数目的确定; 熟练掌握计算单自由度体系自由振动的刚度法和柔度法;掌握 无阻尼单自由度体系在简谐荷载作用下的动力反应的计算方法; 熟练掌握计算两个自由度体系自由振动的刚度法和柔度法;了 解两个自由度体系在简谐荷载作用下的受迫振动;了解阻尼对 振动的影响。 ●本章教学内容的重点:结构动力分析的基本概念;结构的动 力自由度;单自由度体系自由振动微分方程的建立和自振频率 (周期)的计算、二个自由度体系自由振动微分方程的建立和 自振频率、振型的计算;在简谐荷载作用下动位移和动内力的 计算、共振的概念及避免共振的途径。 ●本章教学内容的难点:结构动力自由度;简谐荷载与结构质量 的惯性力作用线不重合时的振动微分方程及动位移、动内力计 算:2对结构强迫振动时动位移各影响因素的分析。 2
16:27:46 2 结构力学—第十二章 结构的动力计算 土木建筑工程学院 2 第十二章、 结构的动力计算 本章导读 ●本章教学的基本要求:掌握结构体系动力自由度数目的确定; 熟练掌握计算单自由度体系自由振动的刚度法和柔度法;掌握 无阻尼单自由度体系在简谐荷载作用下的动力反应的计算方法; 熟练掌握计算两个自由度体系自由振动的刚度法和柔度法;了 解两个自由度体系在简谐荷载作用下的受迫振动;了解阻尼对 振动的影响。 ●本章教学内容的重点: 结构动力分析的基本概念;结构的动 力自由度;单自由度体系自由振动微分方程的建立和自振频率 (周期)的计算、二个自由度体系自由振动微分方程的建立和 自振频率、振型的计算;在简谐荷载作用下动位移和动内力的 计算、共振的概念及避免共振的途径。 ●本章教学内容的难点:结构动力自由度;简谐荷载与结构质量 的惯性力作用线不重合时的振动微分方程及动位移、动内力计 算;对结构强迫振动时动位移各影响因素的分析

结构力学一第十二章结构的动力计算 海南大学士木建筑工程学院 12.1概述 12.1.1结构动力计算的特点 ●动荷载与静荷载的区别 动荷载:大小、方向或位置随时间而变,而且变得很快。 静荷载:大小、方向或位置不随时间而变,或变得很慢。 ●与静力计算的区别 动力荷载作用下的结构计算称为结构动力计算,与静力荷 载计算相比,结构在动力荷载作用下引起的各质点的加速 度以及结构的惯性力是不能忽略的。因此,考虑惯性力的 影响是结构动力学计算最主要的特点。 12.1.2动荷载分类。按起变化规律及其作用特点可分为: (1)周期荷载:随时间作周期性变化。(转动电机的 偏心力)。 16:27:46 3
16:27:46 3 结构力学—第十二章 结构的动力计算 土木建筑工程学院 3 12.1.1结构动力计算的特点 ⚫动荷载与静荷载的区别 动荷载:大小、方向或位置随时间而变, 静荷载:大小、方向或位置不随时间而变, 而且变得很快。 或变得很慢。 ⚫与静力计算的区别 动力荷载作用下的结构计算称为结构动力计算,与静力荷 载计算相比,结构在动力荷载作用下引起的各质点的加速 度以及结构的惯性力是不能忽略的。因此,考虑惯性力的 影响是结构动力学计算最主要的特点。 12.1 概 述 12.1.2动荷载分类。按起变化规律及其作用特点可分为: ( 1)周期荷载:随时间作周期性变化。(转动电机的 偏心力)
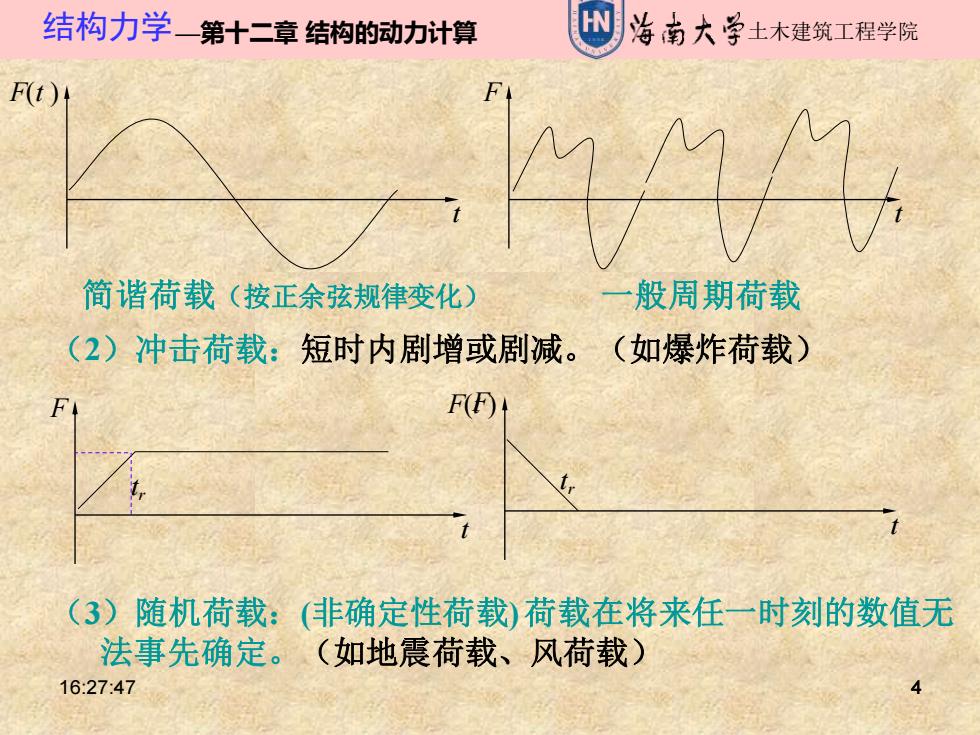
结构力学一第十二章结构的动力计算 治南大学土木建筑工程学院 F(t) 简谐荷载(按正余弦规律变化) 般周期荷载 (2)冲击荷载:短时内剧增或剧减。(如爆炸荷载) F (3)随机荷载:(非确定性荷载)荷载在将来任一时刻的数值无 法事先确定。(如地震荷载、风荷载) 16:2747
16:27:47 4 结构力学—第十二章 结构的动力计算 土木建筑工程学院 4 偏心质量m,偏心距e,匀角速度θ 惯性力:P=m θ2e,其竖向分量和 水平分量均为简谐荷载. θt F(t ) t F t 简谐荷载(按正余弦规律变化) 一般周期荷载 (2)冲击荷载:短时内剧增或剧减。(如爆炸荷载) F t F(t ) t tr tr F (3)随机荷载:(非确定性荷载) 荷载在将来任一时刻的数值无 法事先确定。(如地震荷载、风荷载)
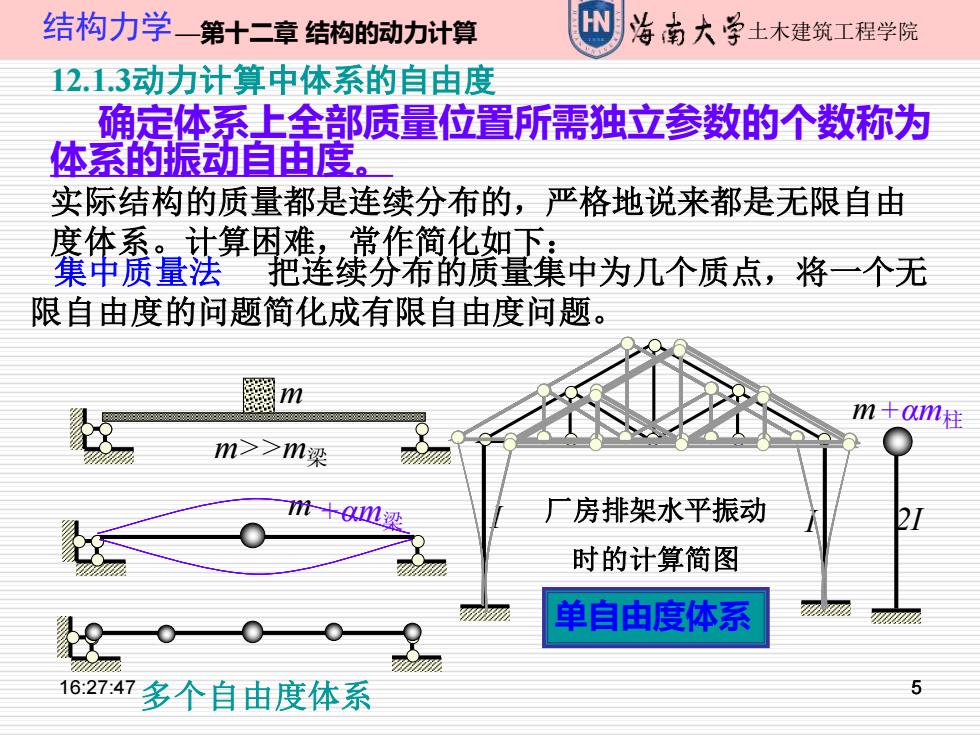
结构力学一第十二章结构的动力计算 W 海南大学土木建筑工程学院 12.1.3动力计算中体系的自由度 确定体系上全部质量位置所需独立参数的个数称为 体系的振动自由度。 实际结构的质量都是连续分布的,严格地说来都是无限自由 度体系。计算困难,常作简化如下: 集中质量法把连续分布的质量集中为几个质点,将一个无 限自由度的问题简化成有限自由度问题。 m m+0m柱 m>>m梁 m+00L梁 厂房排架水平振动 时的计算简图 单自由度体系 162747多个自由度体系 5
16:27:47 5 结构力学—第十二章 结构的动力计算 土木建筑工程学院 5 12.1.3动力计算中体系的自由度 确定体系上全部质量位置所需独立参数的个数称为 体系的振动自由度。 实际结构的质量都是连续分布的,严格地说来都是无限自由 度体系。计算困难,常作简化如下: 集中质量法 把连续分布的质量集中为几个质点,将一个无 限自由度的问题简化成有限自由度问题。 m m>>m梁 m +αm梁 I I 2I m+αm柱 厂房排架水平振动 时的计算简图 单自由度体系 多个自由度体系
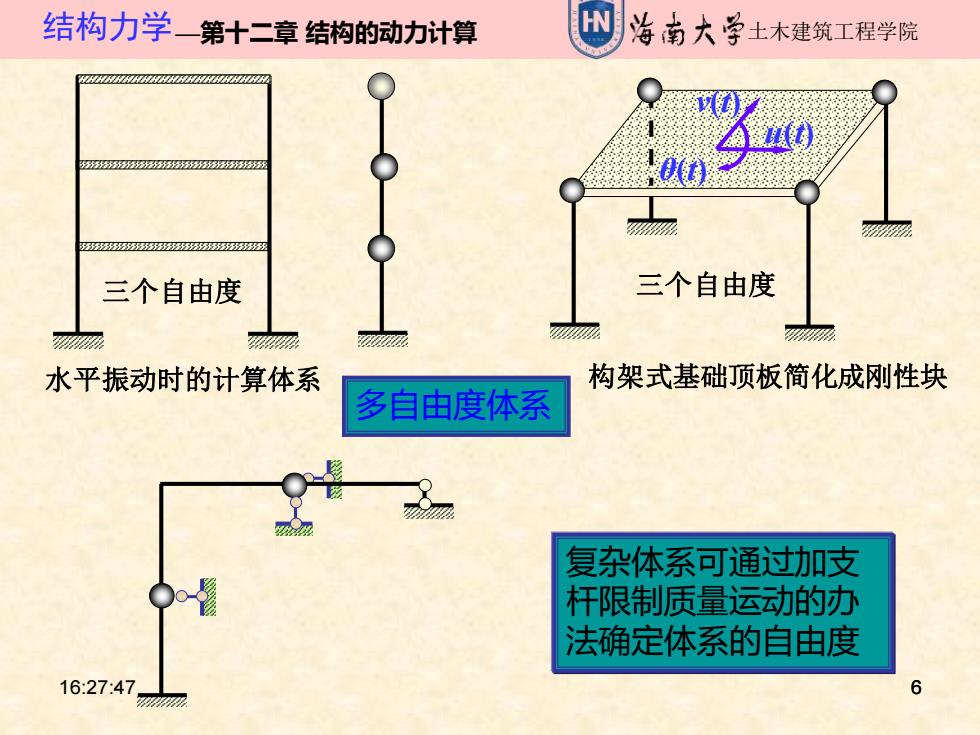
结构力学一第十二章结构的动力计算 W 治南大学土木建筑工程学院 三个自由度 三个自由度 aM远 及 水平振动时的计算体系 构架式基础顶板简化成刚性块 多自由度体系 复杂体系可通过加支 杆限制质量运动的办 法确定体系的自由度 16:27:47 6
16:27:47 6 结构力学—第十二章 结构的动力计算 土木建筑工程学院 6 水平振动时的计算体系 多自由度体系 构架式基础顶板简化成刚性块 θ(t) v(t) u(t) 三个自由度 三个自由度 复杂体系可通过加支 杆限制质量运动的办 法确定体系的自由度