
第章热传导方程 §1 热传导方程及其定解问题的导出 §2 初边值问题的分离变量法 §3 柯西问题 §4 极值原理,定解问题解的唯一性和稳定性 §5 解的渐近性态
第二章 热传导方程 §4 极值原理,定解问题解的唯一性和稳定性 §2 初边值问题的分离变量法 §1 热传导方程及其定解问题的导出 §3 柯西问题 §5 解的渐近性态

§4极值原理,定解问题解的唯一性和稳定性 极值原理 初边值问题解的唯一性和稳定性 3 柯西问题解的唯一性和稳定性 国
§4 极值原理,定解问题解的唯一性和稳定性 1 极值原理 2 初边值问题解的唯一性和稳定性 3 柯西问题解的唯一性和稳定性

1极值原理 定理4.1设u(x,t)在矩形Rr={a≤x≤B,0≤t≤T)上连续,并且 在矩形内部满足热传导方程 au 202u a2 (4.1) at x2 则在矩形的两个侧边(x=α及x=B,0≤t≤T)及底边(t=0,≤ x≤B)上取得最大值和最小值.换言之,若以r表示Rr的边界曲线 (抛物线界),那么成立 maxu(x,t)=maxu(x.t). minu(x,t)=minu(x)
1 极值原理 定理4.1 设𝑢 𝑥,𝑡 在矩形𝑅𝑇 = 𝛼 ≤ 𝑥 ≤ 𝛽, 0 ≤ 𝑡 ≤ 𝑇 上连续,并且 在矩形内部满足热传导方程 𝜕𝑢 𝜕𝑡 = 𝑎 2 𝜕 2𝑢 𝜕𝑥 2 (4.1) 则在矩形的两个侧边 𝑥 = 𝛼及𝑥 = 𝛽, 0 ≤ 𝑡 ≤ 𝑇 及底边ሺ ሻ 𝑡 = 0,𝛼 ≤ 𝑥 ≤ 𝛽 上取得最大值和最小值.换言之,若以𝛤𝑇表示𝑅𝑇的边界曲线 (抛物线界),那么成立 𝑚𝑎𝑥 𝑅𝑇 𝑢 𝑥,𝑡 = max 𝛤𝑇 𝑢 𝑥,𝑡 , min 𝑅𝑇 𝑢 𝑥,𝑡 = min 𝛤𝑇 𝑢 𝑥,𝑡
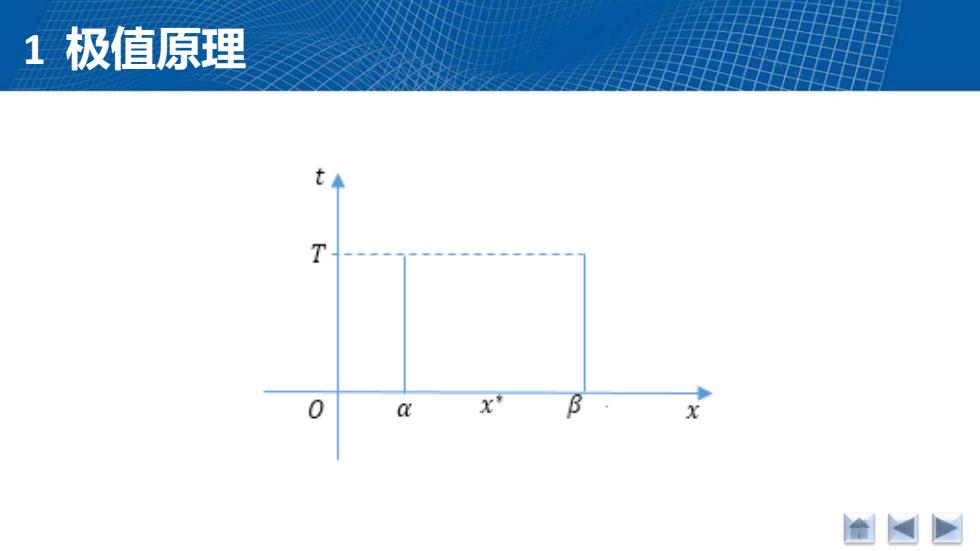
1极值原理 T 国
1 极值原理

1极值原理 证明:只考虑最大值情形即可(反证法) 若令M=maxu(x,t),m=maxu(x,t).若定理不真,那么M>m. RT 此时,在内不一定存在一点(x*,t*)t*>0,<x*<B)使 u(x*,t)=M.作函 G-)(0- 由于在Ir上 M-m M 3 V(x,t)<m+4 +4m=6M(0<0<1) 4 而 V(x*,l*)=M
1 极值原理 证明 : 只考虑最大值情形即可(反证法) 若令𝑀 = 𝑚𝑎𝑥 𝑅𝑇 𝑢 𝑥,𝑡 , 𝑚 = 𝑚𝑎𝑥 𝛤𝑇 𝑢 𝑥,𝑡 .若定理不真,那么𝑀 > 𝑚. 此 时 , 在 内 不 一 定 存 在 一 点 𝑥 ∗ ,𝑡 ∗ 𝑡 ∗ > 0, 𝛼 < 𝑥 ∗ < 𝛽 使 𝑢 𝑥 ∗ ,𝑡 ∗ = 𝑀.作函数 𝑥,𝑡 = 𝑢 𝑥,𝑡 + 𝑀 − 𝑚 4𝑙 2 𝑥 − 𝑥 ∗ 2 𝑙 = 𝜌 − 𝛼 由于在𝛤𝑇上 𝑉 𝑥,𝑡 < 𝑚 + 𝑀 − 𝑚 4 = 𝑀 4 + 3 4 𝑚 = 𝜃𝑀 0 < 𝜃 < 1 而 𝑉 𝑥 ∗ , 𝑙 ∗ = 𝑀