
高教社全国大学生数学建模竟赛 数学建模竞赛的相关介绍 1.Mcm/lcm国际数学建模竞赛 现代社会的发展,需要数学理论与方法,但更需要熟悉 各种数学方法,能够与物理学家、工程师等合作,能够 解决实际问题的专家。另外,计算机的发展已经能够进 行复杂计算、或者是大数据量计算,这就使得在大学理 工科学生中推广数学建模教学成为可能。 例如,1985年,美国人直接将数学建模课引入理科、 理工科大学生的教学中,并设立了一年一次的“大学生 数学建模竞赛”,简记为MCM。 5/17/2014

高教社全国大学生数学建模竟赛 数学建模介绍 将数学方法应用到任何一个实际问题中去, 往往首先是要把这个问题的内在规律用数字、 图表或公式、符号来表示出来,然后经过数学 的处理得到定量的结果,以供人们作分析、预 报、决策或者控制。这个过程就是通常所说的 数学建模
高教社全国大学生数学建模竞赛 简单的建模实例 例1一个星级宾馆有150间客房,经过一段时 间的经营实践,该宾馆经理得到一些数据:如 果每间客房定价为160元,住房率为55%;定 价为140元,住房率为65%;定价为120元,住 房率为75%;定价为100元,住房率为85%. 欲使每天收入最高,问每间客房的定价应是多 少?

高教社全国大学生数学建模竟赛 解 经分析,为建立宾馆一天收入的数学模型,可作如下假设: 假设1,在无其它信息时,不妨设每间客房的最高定价为 160元. 假设2,根据提供的数据,设随房价的下降,住房率呈线 性增长 假设3,设宾馆每间客房定价相等。 模型建立 根据题意,设y表示宾馆一天的总收入,x为与160元相比 降价的房价. 由假设2,可得每降低1元房价,住房率增加为10%/20 =0.005 所以,y=150(160-x)(0.55+0.005x) 由于0.55+0.005x≤1,可知0≤x≤90 解模型 整理得:y=-0.75(x-25)2+13668.75
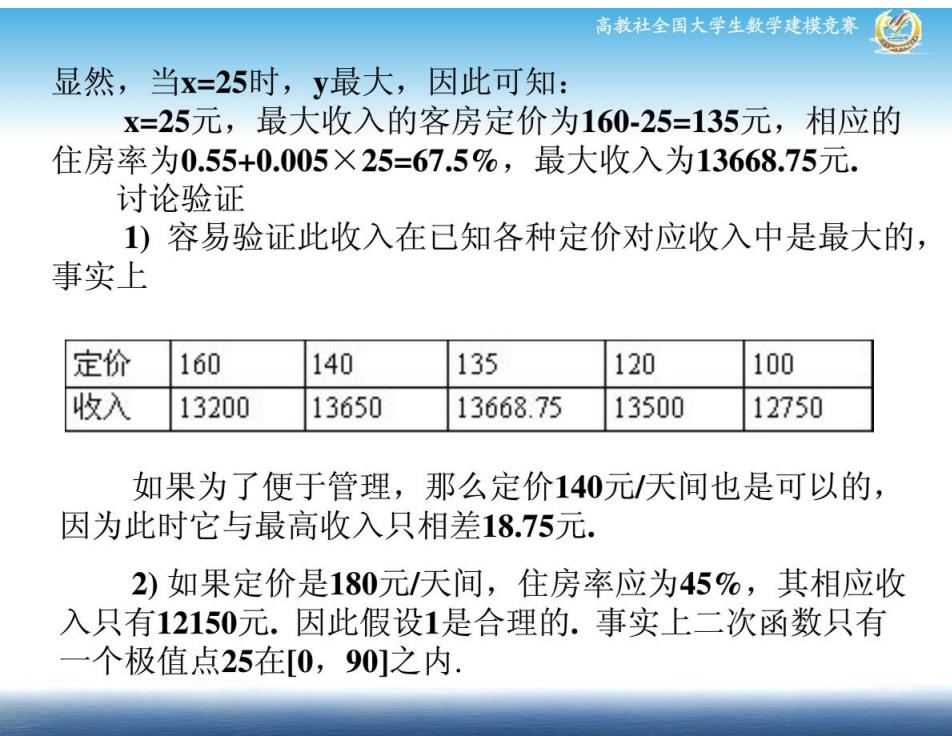
高教社全国大学生数学建模竞赛 显然,当x=25时,y最大,因此可知: x=25元,最大收入的客房定价为160-25=135元,相应的 住房率为0.55+0.005×25=67.5%,最大收入为13668.75元. 讨论验证 1)容易验证此收入在已知各种定价对应收入中是最大的, 事实上 定价 160 140 135 120 100 收入 13200 13650 13668.75 13500 12750 如果为了便于管理,那么定价140元/天间也是可以的, 因为此时它与最高收入只相差18.75元. 2)如果定价是180元/天间,住房率应为45%,其相应收 入只有12150元.因此假设1是合理的.事实上二次函数只有 一个极值点25在[0,90]之内