《经济数学基础》课程PPT教学课件（线性代数）第三章 向量空间（3/4）

2.矩阵秩的求法. 行阶梯形矩阵： 1 1 -2 1 4 1 0 -1 0 4 2 -1 0 0 1 -1 0 例如：A= 3 B= 0 0 0 5 -3 0 0 0 1 -3 0 0 0 0 0 00 0 0 0 特点： (1)可划出一条阶梯线， 线的下方全为零； -2 (2)每个台阶只有一行，台阶 -1 0 数即是非零行的行数，阶梯 -3 线的竖线后面的第一个元素 0 0 0 为非零元，即非零行的第一 个非零元. 11

11 2. 矩阵秩的求法 . 行阶梯形矩阵： 1 0 1 0 4 0 1 1 0 3 0 0 0 1 3 0 0 0 0 0 B   −   − =     −     例如： 1 1 2 1 4 0 2 1 1 0 0 0 0 5 3 0 0 0 0 0 A   −   − =     −     特点： (1)可划出一条阶梯线， 线的下方全为零； (2)每个台阶只有一行，台阶 数即是非零行的行数，阶梯 线的竖线后面的第一个元素 为非零元，即非零行的第一 个非零元． 1 1 2 1 4 0 2 1 1 0 0 0 0 5 3 0 0 0 0 0   −   −     −    

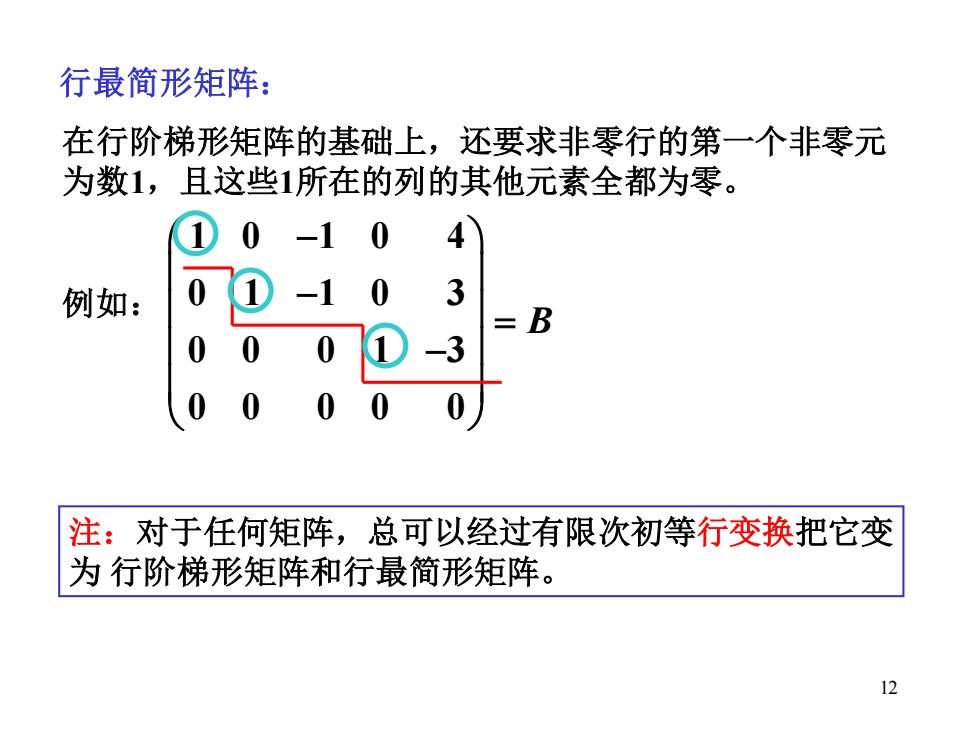
行最简形矩阵： 在行阶梯形矩阵的基础上，还要求非零行的第一个非零元 为数1，且这些1所在的列的其他元素全都为零。 0 -10 例如： 0 -1 0 =B 0 0 3 00 注：对于任何矩阵，总可以经过有限次初等行变换把它变 为行阶梯形矩阵和行最简形矩阵。 12

12 行最简形矩阵： 在行阶梯形矩阵的基础上，还要求非零行的第一个非零元 为数1，且这些1所在的列的其他元素全都为零。 1 0 1 0 4 0 1 1 0 3 0 0 0 1 3 0 0 0 0 0 B   −   −   =   −     例如： 注：对于任何矩阵，总可以经过有限次初等行变换把它变 为 行阶梯形矩阵和行最简形矩阵