第十章数据的统计描述和分析 数理统计研究的对象是受随机因素影响的数据,以下数理统计就简称统计,统计是 以概率论为基础的一门应用学科。 数据样本少则几个,多则成千上万,人们希望能用少数几个包含其最多相关信息的 数值来体现数据样本总体的规律。描述性统计就是搜集、整理 加工和分所统计数 史之系 化、条理化 以显示出数据资料的趋势、特征和数量关系。它是统计推断的基 础,实用性较强 的最方 据如进行 述与分析,需要掌握参数估计和假设检验这两个数理统 我们将用Matlab的统计工具箱(Statisties Toolbox)来实现数据的统计描述和分析。 §1统计的基本概念 1.1 总体和样本 总体是人们研究对象的全体,又称母体,如工厂一天生产的全部产品(按合格品及 废 全体学生的身 为个体,个体的特征用 一个变量(如x)来表示,如 件产品是降随产生的 的集合称为样 子m的学 名 生的身高,或者一根轴直径的10次测量。实际上这就是从总体中随机取得的一批数据 不妨记作x n称为样本容量 简单地说,统计的任务是由样本推断总体, 且万 主是杂乱无章的,做出它的频数表和直方图,可以看作是对这 以数据的取值为横坐标, 个阶梯形的图,称为直方图,或频数分布图 若样本容量不大,能够手工做出频数表和直方图,当样本容量较大时则可以借助 Matlab这样的软件了。让我们以下面的例子为例,介绍频数表和直方图的作法。 例】学生的身高和体重 学校随机抽取100名学生,测量他们的身高和体重,所得数据如表 身高体重身高体重 身高 体重身高体 64 1 58 173 165 176 63 -201
-201- 第十章 数据的统计描述和分析 数理统计研究的对象是受随机因素影响的数据,以下数理统计就简称统计,统计是 以概率论为基础的一门应用学科。 数据样本少则几个,多则成千上万,人们希望能用少数几个包含其最多相关信息的 数值来体现数据样本总体的规律。描述性统计就是搜集、整理、加工和分析统计数据, 使之系统化、条理化,以显示出数据资料的趋势、特征和数量关系。它是统计推断的基 础,实用性较强,在统计工作中经常使用。 面对一批数据如何进行描述与分析,需要掌握参数估计和假设检验这两个数理统计 的最基本方法。 我们将用 Matlab 的统计工具箱(Statistics Toolbox)来实现数据的统计描述和分析。 §1 统计的基本概念 1.1 总体和样本 总体是人们研究对象的全体,又称母体,如工厂一天生产的全部产品(按合格品及 废品分类),学校全体学生的身高。 总体中的每一个基本单位称为个体,个体的特征用一个变量(如 x )来表示,如一 件产品是合格品记 x = 0 ,是废品记 x = 1;一个身高 170(cm)的学生记 x = 170。 从总体中随机产生的若干个个体的集合称为样本,或子样,如n 件产品,100 名学 生的身高,或者一根轴直径的 10 次测量。实际上这就是从总体中随机取得的一批数据, 不妨记作 n x , x , , x 1 2 L ,n 称为样本容量。 简单地说,统计的任务是由样本推断总体。 1.2 频数表和直方图 一组数据(样本)往往是杂乱无章的,做出它的频数表和直方图,可以看作是对这 组数据的一个初步整理和直观描述。 将数据的取值范围划分为若干个区间,然后统计这组数据在每个区间中出现的次 数,称为频数,由此得到一个频数表。以数据的取值为横坐标,频数为纵坐标,画出一 个阶梯形的图,称为直方图,或频数分布图。 若样本容量不大,能够手工做出频数表和直方图,当样本容量较大时则可以借助 Matlab 这样的软件了。让我们以下面的例子为例,介绍频数表和直方图的作法。 例 1 学生的身高和体重 学校随机抽取 100 名学生,测量他们的身高和体重,所得数据如表 表 1 身高体重数据 身高 体重 身高 体重 身高 体重 身高 体重 身高 体重 172 75 169 55 169 64 171 65 167 47 171 62 168 67 165 52 169 62 168 65 166 62 168 65 164 59 170 58 165 64 160 55 175 67 173 74 172 64 168 57 155 57 176 64 172 69 169 58 176 57 173 58 168 50 169 52 167 72 170 57 166 55 161 49 173 57 175 76 158 51 170 63 169 63 173 61 164 59 165 62 167 53 171 61 166 70 166 63 172 53 173 60 178 64 163 57 169 54 169 66 178 60 177 66 170 56 167 54 169 58 173 73 170 58 160 65 179 62 172 50 163 47 173 67 165 58 176 63 162 52

57177 99 160 177 64184 70 16649 1717117059 (i)数据输入 数据输入通常有两种方法,一种是在交互环境中直接输入,如果在统计中数据量比 这大高样的表大0金种是用 可用 具体作 这样在内存中建立了一个变量data,它是一个包含有20×10个数据的矩阵。 为了得到我们需要的100个身高和体重各为一列的矩阵,应做如下的改变: high=data(:,1:2:9);high=high(: )作表及直方 );weight=weight (: 求须数用hist命令实现,其用法是: IN XI=hist(Y M 得到数组(行、列均可)Y的频数表。它将区间min(Y),maxY】等分为M份(缺省时 M设定为10),N返回M个小区间的频数,X返回M个小区间的中点。 画出数组Y的直方图。 对于例1的数据,编写程序如下 load data.txt; high=data (:,1: 22ii9tettigte): nist (high) 号下面语句与hist命令 价 9161.2)) length(find(high>=170.7shigh<17 tn2,2hit(we1ght) subplot (1,2,1),hist (high) 计算结果略,直方图如图1所示 202
-202- 165 66 172 59 177 66 182 69 175 75 170 60 170 62 169 63 186 77 174 66 163 50 172 59 176 60 166 76 167 63 172 57 177 58 177 67 169 72 166 50 182 63 176 68 172 56 173 59 174 64 171 59 175 68 165 56 169 65 168 62 177 64 184 70 166 49 171 71 170 59 (i) 数据输入 数据输入通常有两种方法,一种是在交互环境中直接输入,如果在统计中数据量比 较大,这样作不太方便;另一种办法是先把数据写入一个纯文本数据文件 data.txt 中, 格式如例 1 的表 1,有 20 行、10 列,数据列之间用空格键或 Tab 键分割,该数据文件 data.txt 存放在 matlab\work 子目录下,在 Matlab 中用 load 命令读入数据,具体作法是: load data.txt 这样在内存中建立了一个变量 data,它是一个包含有20×10 个数据的矩阵。 为了得到我们需要的 100 个身高和体重各为一列的矩阵,应做如下的改变: high=data(:,1:2:9);high=high(:) weight=data(:,2:2:10);weight=weight(:) (ii)作频数表及直方图 求频数用 hist 命令实现,其用法是: [N,X] = hist(Y,M) 得到数组(行、列均可)Y 的频数表。它将区间[min(Y),max(Y)]等分为 M 份(缺省时 M 设定为 10),N 返回 M 个小区间的频数,X 返回 M 个小区间的中点。 命令 hist(Y,M) 画出数组 Y 的直方图。 对于例 1 的数据,编写程序如下: load data.txt; high=data(:,1:2:9);high=high(:); weight=data(:,2:2:10);weight=weight(:); [n1,x1]=hist(high) %下面语句与hist命令等价 %n1=[length(find(high<158.1)),. % length(find(high>=158.1&high<161.2)),. % length(find(high>=161.2&high<164.5)),. % length(find(high>=164.5&high<167.6)),. % length(find(high>=167.6&high<170.7)),. % length(find(high>=170.7&high<173.8)),. % length(find(high>=173.8&high<176.9)),. % length(find(high>=176.9&high<180)),. % length(find(high>=180&high<183.1)),. % length(find(high>=183.1))] [n2,x2]=hist(weight) subplot(1,2,1), hist(high) subplot(1,2,2), hist(weight) 计算结果略,直方图如图 1 所示
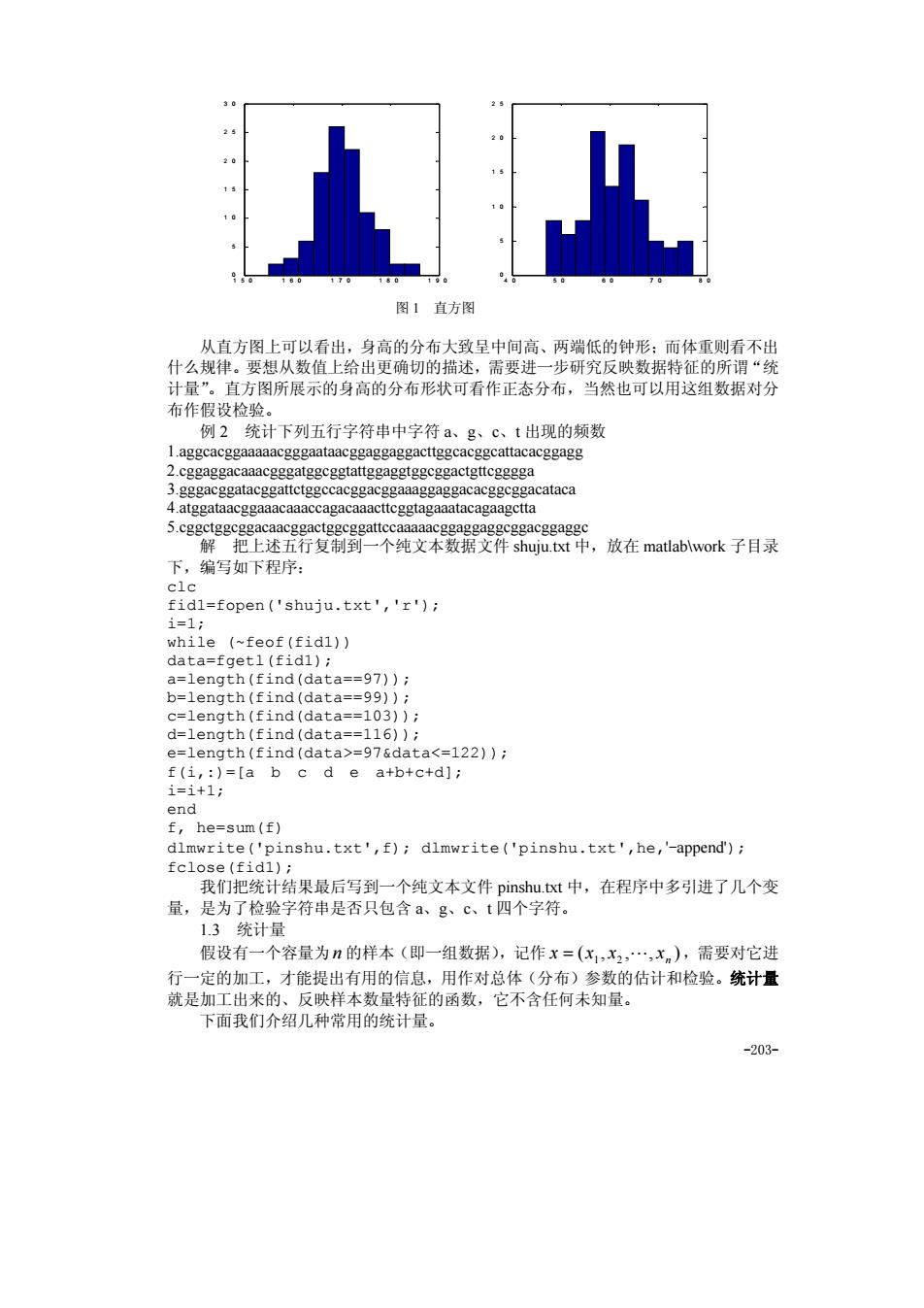
图1直方图 从直方图上可以看出,身高的分布大致呈中间高、两端低的钟形:而体重则看不出 什么规律。要想从数值上给出更确切的描述,需要进一步研究反映数据特征的所谓“纨 计量”。直方图所展示的身高的分布形状可看作正态分布,当然也可以用这组数据对分 布作假设检验。 例2统计下列五行字符串中字符a、g、c、t出现的频数 aggcacggaaaaacgggaataac ggac cataca ,5c3觉述置器复新蜀"个纯文本数据受释革,放在matabwork子目录 下,编写如下程序: idi-fopen ('shj) 1=1 b=length(find(data==99)); d=length(find(data==116)); e=length(find(data>=976data<=122)); end inshu.txt',f);dimwrite('pinshu.txt',he,'-append); fclose (fidl) 我们把统计结果最后写到一个纯文本文件pinshu.txt中,在程序中多引进了几个变 量,是为了检验字符串是否只包含a、g、ct四个字符。 1.3统计量 假设有一个容量为n的样本(即一组数据),记作x=(x,x2,.,xn),需要对它进 行一定的加工,才能提出有用的信息,用作对总体(分布)参数的估计和检验。统计量 就是加工出来的、反映样本数量特征的函数,它不含任何未知量。 下面我们介绍几种常用的统计量。 -203
-203- 150 160 170 180 190 0 5 1 0 1 5 2 0 2 5 3 0 4 0 5 0 6 0 7 0 8 0 0 5 1 0 1 5 2 0 2 5 图 1 直方图 从直方图上可以看出,身高的分布大致呈中间高、两端低的钟形;而体重则看不出 什么规律。要想从数值上给出更确切的描述,需要进一步研究反映数据特征的所谓“统 计量”。直方图所展示的身高的分布形状可看作正态分布,当然也可以用这组数据对分 布作假设检验。 例 2 统计下列五行字符串中字符 a、g、c、t 出现的频数 1.aggcacggaaaaacgggaataacggaggaggacttggcacggcattacacggagg 2.cggaggacaaacgggatggcggtattggaggtggcggactgttcgggga 3.gggacggatacggattctggccacggacggaaaggaggacacggcggacataca 4.atggataacggaaacaaaccagacaaacttcggtagaaatacagaagctta 5.cggctggcggacaacggactggcggattccaaaaacggaggaggcggacggaggc 解 把上述五行复制到一个纯文本数据文件 shuju.txt 中,放在 matlab\work 子目录 下,编写如下程序: clc fid1=fopen('shuju.txt','r'); i=1; while (~feof(fid1)) data=fgetl(fid1); a=length(find(data==97)); b=length(find(data==99)); c=length(find(data==103)); d=length(find(data==116)); e=length(find(data>=97&data<=122)); f(i,:)=[a b c d e a+b+c+d]; i=i+1; end f, he=sum(f) dlmwrite('pinshu.txt',f); dlmwrite('pinshu.txt',he,'-append'); fclose(fid1); 我们把统计结果最后写到一个纯文本文件 pinshu.txt 中,在程序中多引进了几个变 量,是为了检验字符串是否只包含 a、g、c、t 四个字符。 1.3 统计量 假设有一个容量为n 的样本(即一组数据),记作 ( , , , ) 1 2 n x = x x L x ,需要对它进 行一定的加工,才能提出有用的信息,用作对总体(分布)参数的估计和检验。统计量 就是加工出来的、反映样本数量特征的函数,它不含任何未知量。 下面我们介绍几种常用的统计量

之 (1) 中位数是将数据由小到大排序后位于中间位置的那个数值 返回x的均值,median(x)返回中位数。 ()表示变异程度的统计量一标准差、方差和极差 标准差s定义为 (2) n-1 它是各个数据与均值偏离程度的度量,这种偏离不妨称为变异。 方差是标准差的平方s。 极差是x=(x1, ·,x)的最大值与最小值之差。 Matlab中std(x)返回x的标准差,varx)返回方差,range(x)返回极差, 你可能注意到标准差s的定义(2)中,对n个(x,-)的平方求和,却被(n-1)除, 这是出于无偏估计的要求。若需要改为被n除,Matlab可用std(x,l)和var(x,l)来实现。 ()中心矩、表示分布形状的统计量一偏度和修度 防机变量x的r阶中心矩为E(x一Ex)。 随机变量x的偏度和峰度指的是x的标准化变量(x一Ex)/√Dx的三阶中心矩和 四阶中心矩: =E -Ey)7 E(x-E(x) D() (D(x西 x-E(x) E(x-E(x)) V,=E √Dx) (D(x)) 偏度反映分布的对称性,片>0称为右偏态,此时数据位于均值右边的比位于左 边的多:y<0称为左偏态,情况相反:而y接近0则可认为分布是对称的。 蜂度是分布形状的另一种度量,正态分布的峰度为3,若比3大得多,表示分布 的四 说明样本中含有较多远离均值的数据,因而峰度可以用作衡量偏离正态 Mat lab中 nt(x,order)返回x的order阶中心矩,order为中心矩的阶数。 ess)返回x的偏度,ku is(x)返回峰度。 在以上用阳1b计算各个统计量的命令中,若x为矩阵,则作用于x的列,返回 一个行向量。 对例1给出的学生身高和体重,用Matlab计算这些统计量,程序如下: cled data.tx high=data(:,1:2:9);high=high(:) weight=data(:,2:2:10);weight=weight(:); -204-
-204- (i)表示位置的统计量—算术平均值和中位数 算术平均值(简称均值)描述数据取值的平均位置,记作 x , ∑= = n i i x n x 1 1 (1) 中位数是将数据由小到大排序后位于中间位置的那个数值。 Matlab 中 mean(x)返回 x 的均值,median(x)返回中位数。 (ii)表示变异程度的统计量—标准差、方差和极差 标准差 s 定义为 2 1 1 2 ( ) 1 1 ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ − − = ∑= n i i x x n s (2) 它是各个数据与均值偏离程度的度量,这种偏离不妨称为变异。 方差是标准差的平方 2 s 。 极差是 ( , , , ) 1 2 n x = x x L x 的最大值与最小值之差。 Matlab 中 std(x)返回 x 的标准差,var(x)返回方差,range(x)返回极差。 你可能注意到标准差 s 的定义(2)中,对n 个(x x) i − 的平方求和,却被(n −1) 除, 这是出于无偏估计的要求。若需要改为被n 除,Matlab 可用 std(x,1)和 var(x,1)来实现。 (iii)中心矩、表示分布形状的统计量—偏度和峰度 随机变量 x 的 r 阶中心矩为 r E(x − Ex) 。 随机变量 x 的偏度和峰度指的是 x 的标准化变量(x − Ex)/ Dx 的三阶中心矩和 四阶中心矩: [( ) ] ( ) , ( ) ( ) ( ) ( ) 3/ 2 3 3 1 D x E x E x D x x E x E − = ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ − ν = [( ) ] ( ) . ( ) ( ) ( ) ( ) 2 4 4 2 D x E x E x D x x E x E − = ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ − ν = 偏度反映分布的对称性, 0 ν 1 > 称为右偏态,此时数据位于均值右边的比位于左 边的多; 0 ν 1 < 称为左偏态,情况相反;而ν 1接近 0 则可认为分布是对称的。 峰度是分布形状的另一种度量,正态分布的峰度为 3,若ν 2 比 3 大得多,表示分布 有沉重的尾巴,说明样本中含有较多远离均值的数据,因而峰度可以用作衡量偏离正态 分布的尺度之一。 Matlab 中 moment(x,order)返回 x 的 order 阶中心矩,order 为中心矩的阶数。 skewness(x)返回 x 的偏度,kurtosis(x)返回峰度。 在以上用 Matlab 计算各个统计量的命令中,若 x 为矩阵,则作用于 x 的列,返回 一个行向量。 对例 1 给出的学生身高和体重,用 Matlab 计算这些统计量,程序如下: clc load data.txt; high=data(:,1:2:9);high=high(:); weight=data(:,2:2:10);weight=weight(:);

an(shuju) biao Zhun cha-sto (shuju) pian du-skevness (huj) feng_du=kurtosis(shuju) 统计量中最重要、最常用的是均值和标准差,由于样本是随机变量,它们作为样本 的函数自然也是随机变量,当用它们去推新总体时,有多大的可靠性就与统计量的概率 分布有关,因此我们需要知道几个重要分布的简单性质。 1.4统计中几个重要的概率分布 141 分布函数 ,密度函数和分位数 随机变量的特性完全由它的(概率)分布函数或(概率)密度函数来描述。设有随 机变量X,其分布函数定义为X≤x的概率,即F(x)=P{X≤x}。若X是连续型随 机变量,则其密度函数p(x)与F(x)的关系为 F(x)=[p(x)dx. 上:分位数是下面常用的一个概念,其定义为:对于0<口<1,使某分布函数 F(x)=1-a的x,称为这个分布的上a分位数,记作x。 我们前面画过的直方图品顿数分布图数除以样本容员n,称为频率, 率是得李的折似,因此有方图可以看作密府函数图形的《高微化牵, 142统计中几个重要的概率分布 (i)正态分而 正态分布随机变量X的密度函数曲线呈中间高两边低、对称的钟形,期望(均值) EX=4,方差DX=G2,记作X~N(4,o2),g称均方差或标准差,当4=0,g=1 时称为标准正态分布,记作X、N(O,1)。正态分布完全由均值和方差决定,它 的偏度为0,蜂度为3 正态 布可以说是最 常见的(连续型)概率分布,成批生产时零件的尺寸,射击 弹着点的 然界 成的有 者深刻的理 相雪 鉴于正态分布的随机变量在 生活中如此地常见, 580% 的数值落在距均值左右1个标准差的范围内, 即 P{-o≤X≤+a}=0.68: 95%的数值落在距均值左右2个标准差的范围内,即 42}=0 99.7%的数值落有 左石3 标准差 范围内,即 P{u-3o≤X≤u+3o}=0.99 (ii)x2分布(Chi square) 若X,X2,X为相互独立的、服从标准正态分布N(0,)的随机变量,则它们的 平方和了=立X服从X2分布,记作了~x),n称自由度,它的期望EY=n, -205
-205- shuju=[high weight]; jun_zhi=mean(shuju) zhong_wei_shu=median(shuju) biao_zhun_cha=std(shuju) ji_cha=range(shuju) pian_du=skewness(shuju) feng_du=kurtosis(shuju) 统计量中最重要、最常用的是均值和标准差,由于样本是随机变量,它们作为样本 的函数自然也是随机变量,当用它们去推断总体时,有多大的可靠性就与统计量的概率 分布有关,因此我们需要知道几个重要分布的简单性质。 1.4 统计中几个重要的概率分布 1.4.1 分布函数、密度函数和分位数 随机变量的特性完全由它的(概率)分布函数或(概率)密度函数来描述。设有随 机变量 X ,其分布函数定义为 X ≤ x 的概率,即 F(x) = P{X ≤ x}。若 X 是连续型随 机变量,则其密度函数 p(x) 与 F(x) 的关系为 ∫−∞ = x F(x) p(x)dx . 上α 分位数是下面常用的一个概念,其定义为:对于0 <α <1,使某分布函数 F(x) =1−α 的 x ,称为这个分布的上α 分位数,记作 α x 。 我们前面画过的直方图是频数分布图,频数除以样本容量n ,称为频率,n 充分大 时频率是概率的近似,因此直方图可以看作密度函数图形的(离散化)近似。 1.4.2 统计中几个重要的概率分布 (i)正态分布 正态分布随机变量 X 的密度函数曲线呈中间高两边低、对称的钟形,期望(均值) EX = μ ,方差 2 DX = σ ,记作 ~ ( , ) 2 X N μ σ ,σ 称均方差或标准差,当 μ = 0,σ = 1 时称为标准正态分布,记作 X ~ N(0,1) 。正态分布完全由均值 μ 和方差 2 σ 决定,它 的偏度为 0,峰度为 3。 正态分布可以说是最常见的(连续型)概率分布,成批生产时零件的尺寸,射击中 弹着点的位置,仪器反复量测的结果,自然界中一种生物的数量特征等,多数情况下都 服从正态分布,这不仅是观察和经验的总结,而且有着深刻的理论依据,即在大量相互 独立的、作用差不多大的随机因素影响下形成的随机变量,其极限分布为正态分布。 鉴于正态分布的随机变量在实际生活中如此地常见,记住下面 3 个数字是有用的: 68%的数值落在距均值左右 1 个标准差的范围内,即 P{μ −σ ≤ X ≤ μ +σ} = 0.68; 95%的数值落在距均值左右 2 个标准差的范围内,即 P{μ − 2σ ≤ X ≤ μ + 2σ} = 0.95 ; 99.7%的数值落在距均值左右 3 个标准差的范围内,即 P{μ − 3σ ≤ X ≤ μ + 3σ} = 0.997 . (ii) 2 χ 分布(Chi square) 若 X X Xn , , , 1 2 L 为相互独立的、服从标准正态分布 N(0,1) 的随机变量,则它们的 平方和 ∑= = n i Y Xi 1 2 服从 2 χ 分布,记作 ~ ( ) 2 Y χ n , n 称自由度,它的期望 EY = n