(3)非零常数k乘以第行后加到第行上 0 A- 4. &i k灯 =A aj+ka; 显然,A,中的行向量组 可以由A的行向量组线性表示 m 而A的行向量组可以由 A中的行向量组线性表示。 所以两个向量组等价,所以行向量组的秩不变, 所以矩阵的行秩不变。 6
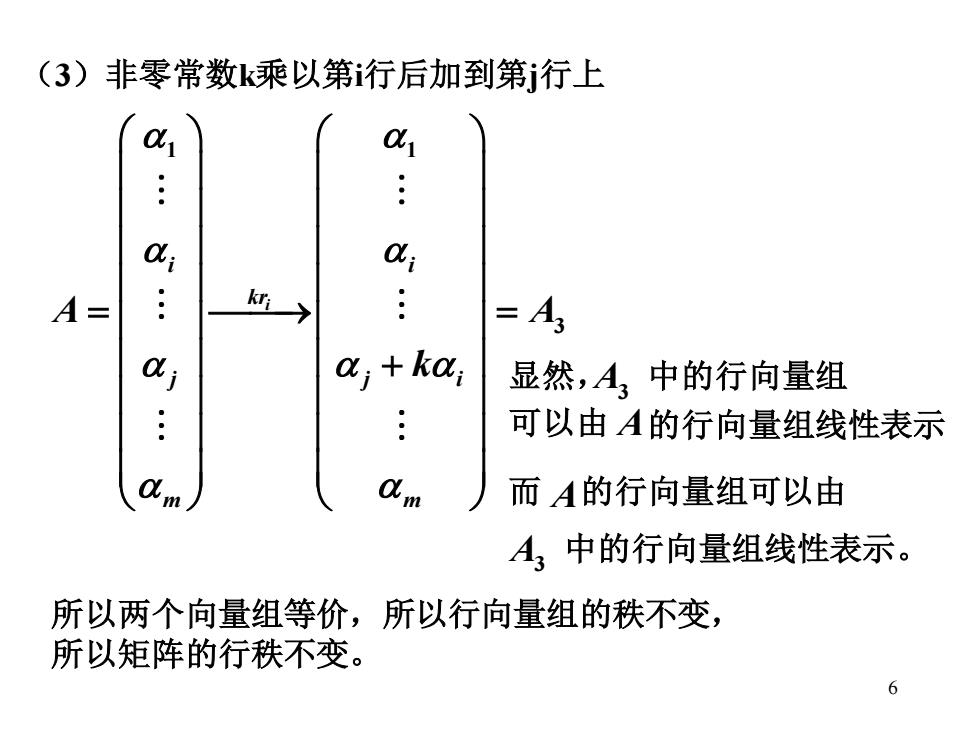
6 (3)非零常数k乘以第i行后加到第j行上 1 1 3 i i i kr j j i m m A A k = ⎯⎯→ = + 显然, A3 中的行向量组 可以由 A 的行向量组线性表示 而 A 的行向量组可以由 A3 中的行向量组线性表示。 所以两个向量组等价,所以行向量组的秩不变, 所以矩阵的行秩不变

引理2:矩阵的初等行变换不改变矩阵的列秩。 (列) (行) 证:设矩阵A经过初等行变换变为B, 即存在有限个初等矩阵P,P2,.,P 使得PP.PA=B 令P=PP.P则PA=B 把Axm按列分块,设Amxn=(a1,02,.,Cn) 不妨设A的列向量组的极大无关组为01,2,.,0, (可交换列的次序把它们换到前列,矩阵的秩不变) 则PA=P(a1,a2,.,an)=(Pa,Pa2,.,Pan) =B
7 引理2:矩阵的初等行变换不改变矩阵的列秩。 (列) (行) 证:设矩阵A经过初等行变换变为B, 即存在有限个初等矩阵 1 2 , , , P P PS 使得 P P P A B 1 2 S = 令 P P P P = 1 2 S 则 PA B = 把 A m n 按列分块,设 1 2 ( , , , ) A m n n = 不妨设A的列向量组的极大无关组为 1 2 , , , , r (可交换列的次序把它们换到前r列,矩阵的秩不变) 则 1 2 1 2 ( , , , ) ( , , , ) PA P P P P = = n n = B

下面证明A的列向量组的极大无关组C1,C2,.,0C, 经过初等行变换变为Pa,Pa2,.,Pa, 是矩阵B的列向量组的极大无关组。 (1)先证Pac1,Pa2,Pa,线性无关。 设数k1,k2,.,k, 使得kPa1+k2Pa2+k,Pan=0成立 P(k1+kc2+k,C)=0 因为P为初等矩阵的乘积,所以P可逆。 .P-P(k a+kaz +ka,)=P-0 ∴.k1+k2a2+k,Qn=0又a1,02,.,0,线性无关 .k1=k2=k3=0.Pa1,PC2,.,PC,线性无关。8
8 下面证明A的列向量组的极大无关组 1 2 , , , r 经过初等行变换变为 1 2 , , , P P P r 是矩阵B的列向量组的极大无关组。 (1)先证 1 2 , , , P P P r 线性无关。 设数 1 2 , , , r k k k 使得 1 1 2 2 0 r r k P k P k P + + = 成立 1 1 2 2 ( ) 0 P k k k + + = r r 因为P为初等矩阵的乘积,所以P可逆。 1 1 1 1 2 2 ( ) 0 P P k k k P r r − − + + = 1 1 2 2 0 r r + + = k k k 又 1 2 , , , r 线性无关 1 2 3 = = = k k k 0 1 2 , , , P P P r 线性无关

(2)再证B的列向量组中任一向量P, 可由向量组Pa1,Pa2,.,Pa,线性表示。 ,C1,02,.,c,是A的列向量组的极大无关组 所以对于A中任一列向量都存在数1,2,1, 使得=l11+l2a2+.+1,a, 等号两边左乘P 有Pa,=l1Pa,+lPa2+.+l,Pa, 由(1)(2)可知Pa1,Pa2,.,Pa,是B的列向量组的一个极大 无关组。 所以,B的列秩=r=A的列秩 9
9 (2)再证B的列向量组中任一向量 P j 可由向量组 1 2 , , , P P P r 线性表示。 1 2 , , , r 是A的列向量组的极大无关组 所以对于A中任一列向量 1 2 , , , r j 都存在数 l l l 使得 j r r 1 1 2 2 = + + + l l l 等号两边左乘P 有 P l P l P l P j r r = + + + 1 1 2 2 由(1)(2)可知 1 2 , , , P P P r 是B的列向量组的一个极大 无关组。 所以,B的列秩=r=A的列秩

综上,矩阵的初等变换不改变矩阵的行秩与列秩。 定理:矩阵的行秩=矩阵的列秩 证:任何矩阵A都可经过初等变换变为 E, 0 形式, 而它的行秩为r,列秩也为r。 又,初等变换不改变矩阵的行秩与列秩, 所以,A的行秩=r=A的列秩 定义2:矩阵的行秩=矩阵的列秩,统称为矩阵的秩。 记为r(A),或rankA,或秩A。 推论:矩阵的初等变换不改变矩阵的秩。 10
10 综上,矩阵的初等变换不改变矩阵的行秩与列秩。 定理:矩阵的行秩=矩阵的列秩 证:任何矩阵A都可经过初等变换变为 0 0 0 E r 形式, 而它的行秩为r,列秩也为r。 又,初等变换不改变矩阵的行秩与列秩, 所以,A的行秩=r=A的列秩 定义2:矩阵的行秩=矩阵的列秩,统称为矩阵的秩。 记为r(A),或rankA,或秩A。 推论:矩阵的初等变换不改变矩阵的秩